В данной публикации мы рассмотрим, какие векторы называются ортогональными, какое условие при этом должно выполняться. Также разберем примеры решения задач по этой теме.
- Условие ортогональности векторов
- Примеры задач
- Ортогональность векторов. Перпендикулярность векторов.
- Примеры задач на ортогональность векторов
- Примеры плоских задач на ортогональность векторов
- Примеры пространственных задач на ортогональность векторов
- Ортогональные векторы и условие ортогональности
- Ортогональные векторы: определение и условие
- Примеры решения задач на ортогональность векторов
- Плоские задачи на ортогональность векторов
- Примеры пространственных задач на ортогональность векторов
Условие ортогональности векторов
Векторы a и b являются ортогональными, если угол между ними прямой (т.е. равен 90°).
Примечание: Скалярное произведение ортогональных векторов равняется нулю. Это и есть существенное условие их ортогональности.
a · b = 0
То есть, если в плоскости и , то
Примеры задач
Задание 1
Докажем, что векторы и ортогональны.
Решение:
a · b = 2 · (-2) + 4 · 1 = 0
Следовательно, заданные векторы являются ортогональными, так как их скалярное произведение равняется нулю.
Задание 2
При каком значении n векторы и ортогональны.
Решение:
a · b = 3 · 6 + (-9) · n = 0
18 – 9n = 0
n = 2
Таким образом, a и b ортогональны при n, равном двум.
Ортогональность векторов. Перпендикулярность векторов.
Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1).
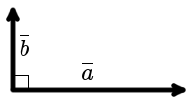 |
| рис. 1 |
Примеры задач на ортогональность векторов
Примеры плоских задач на ортогональность векторов
Так в случае плоской задачи для векторов a = < ax ; ay > и b = < bx ; by > , условие ортогональности запишется следующим образом:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) = 2 — 2 = 0
Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Найдем скалярное произведение этих векторов:
a · b = 3 · 7 + (-1) · 5 = 21 — 5 = 16
Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 = 2 n + 4
2 n + 4 = 0
2 n = -4
n = -2
Ответ: вектора a и b будут ортогональны при n = -2.
Примеры пространственных задач на ортогональность векторов
Так в случае пространственной задачи для векторов a = < ax ; ay ; az > и b = < bx ; by ; bz >, условие ортогональности запишется следующим образом:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 — 2 + 0 = 0
Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Найдем скалярное произведение этих векторов:
a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0
Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 + 1 · (-8)= 2 n + 4 — 8 = 2 n — 4
2 n — 4 = 0
2 n = 4
n = 2
Ответ: вектора a и b будут ортогональны при n = 2.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Ортогональные векторы и условие ортогональности
В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.
Ортогональные векторы: определение и условие
Ортогональные векторы — это векторы a ¯ и b ¯ , угол между которыми равен 90 0 .
Необходимое условие для ортогональности векторов — два вектора a ¯ и b ¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.
Примеры решения задач на ортогональность векторов
Плоские задачи на ортогональность векторов
Если дана плоская задача, то ортогональность для векторов a ¯ = и b ¯ = записывают следующим образом:
a ¯ × b ¯ = a x × b x + a y × b y = 0
Задача 1. Докажем, что векторы a ¯ = и b ¯ = ортогональны.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) = 2 — 2 = 0
Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.
Задача 2. Докажем, что векторы a ¯ = и b ¯ = ортогональны.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 3 × 7 + ( — 1 ) × 5 = 21 — 5 = 16
Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.
Задача 3. Найдем значение числа n , при котором векторы a ¯ = и b ¯ = будут ортогональными.
Как решить?
Найдем скалярное произведение данных векторов:
a ¯ × b ¯ = 2 × n + 4 × 1 = 2 n + 4 2 n + 4 = 0 2 n = — 4 n = — 2
Ответ: векторы являются ортогональными при значении n = 2 .
Примеры пространственных задач на ортогональность векторов
При решении пространственной задачи на ортогональность векторов a ¯ = и b ¯ = условие записывается следующим образом: a ¯ × b ¯ = a x × b x + a y × b y + a z × b z = 0 .
Задача 4. Докажем, что векторы a ¯ = и b ¯ = являются ортогональными.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 1 × 2 + 2 × ( — 1 ) + 0 × 10 = 2 — 2 = 0
Ответ: поскольку произведение векторов равняется нулю, то они являются ортогональными.
Задача 5. Найдем значение числа n , при котором векторы a ¯ = и b ¯ = будут являться ортогональными.
Как решить?
Находим скалярное произведение данных векторов:
a ¯ × b ¯ = 2 × n + 4 × 1 + 1 × ( — 8 ) = 2 n + 4 — 8 = 2 n — 4 2 n — 4 = 0 2 n = 4 n = 2
Ответ: векторы a ¯ и b ¯ будут ортогональными при значении n = 2 .
