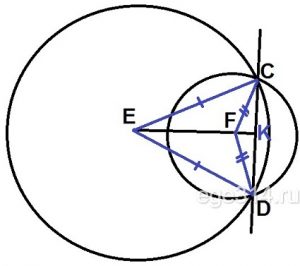
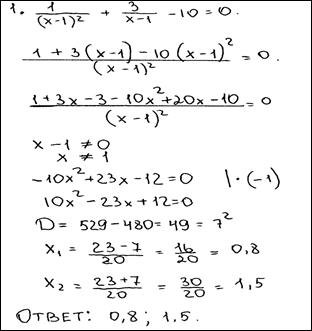Окружности с центрами в точках Е и F пересекаются в точках С и D, причём точки Е и F лежат по одну сторону от прямой СD. Докажите, что CD⊥EF.
Источник задания: ОГЭ 2021 Математика, И.В. Ященко. 36 вариантов.
Построим радиусы ЕС = ED и FC = FD .
Рассмотрим ΔEFC и ΔEFD, в них стороны ЕС = ED и FC = FD, как радиусы окружностей, сторона EF общая. ΔEFC = ΔEFD по трём равным сторонам.
Из равенства треугольников ∠СEF = ∠DEF, значит прямая EF является биссектрисой ∠E, в равнобедренном ΔECD.
Биссектриса равнобедренного треугольника проведённая к основанию так же является и высотой, тогда CD⊥EF.
Что и требовалось доказать.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 1
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
- Репетитор по математике
- Стоимость занятий
- Видеокурсы подготовки к ЕГЭ-2021
- Группа Вконтакте
- Преимущества
- Педагогический стаж
- Собственная методика
- Гарантированный результат
- Индивидуальная работа
- Задание 25 с развернутым ответом повышенного уровня сложности. Задание для самостоятельной работы экспертов.
- 💥 Видео
Видео:ОГЭ Задание 25 Две окружностиСкачать

Репетитор по математике
Меня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата».
Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]
Стоимость занятий
Набор на 2020/2021 учебный год открыт. Предусмотрен дистанционный формат.
Видеокурсы подготовки к ЕГЭ-2021
Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.
Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Группа Вконтакте
В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.
Видео:ОГЭ по математике. Окружности с центрами в точках √25 вариант 2Скачать

Преимущества
Педагогический стаж
Сейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области.
Собственная методика
За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.
Гарантированный результат
За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.
Индивидуальная работа
Все дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал.
Видео:Задача на окружности из ОГЭ-2023!! Разбор за 30 секСкачать

Задание 25 с развернутым ответом повышенного уровня сложности. Задание для самостоятельной работы экспертов.
Задание 1.
Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
Оценка эксперта: ____________________
Задание 2.
Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
Оценка эксперта: ____________________
Задание 3.
Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
Оценка эксперта: ____________________
Задание 4.
Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
Оценка эксперта: ____________________
Задание 25.
| Задание |
| Оценка эксперта |
Задание 26 с развернутым ответом высокого уровня сложности.
Задание для самостоятельной работы экспертов.
Задание 1.
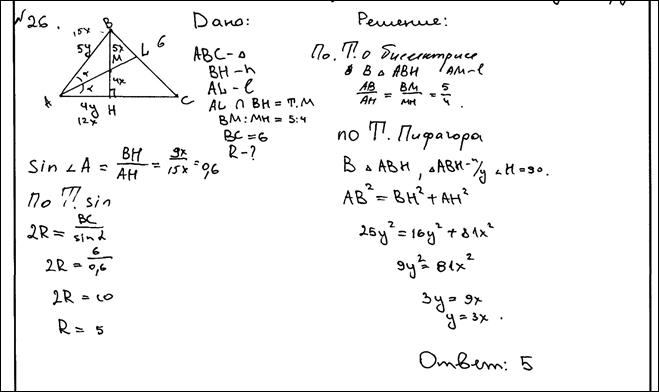
Биссектриса угла A, треугольника ABC делит высоту BH в отношении 5:4, считая от вершины. BC равно 6. Найдите радиус описанной окружности. Ответ: 5.
Оценка эксперта: ____________________
Задание 2.
Биссектриса угла A, треугольника ABC делит высоту BH в отношении 5:4, считая от вершины. BC равно 6. Найдите радиус описанной окружности. Ответ: 5.
Оценка эксперта: ____________________
Задание 3.
Биссектриса угла A, треугольника ABC делит высоту BH в отношении 5:4, считая от вершины. BC равно 6. Найдите радиус описанной окружности. Ответ: 5.
Оценка эксперта: ____________________
Задание 4.
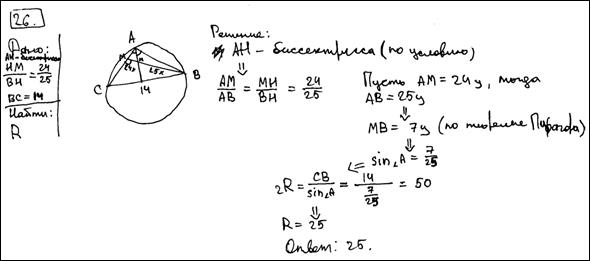
Биссектриса A, треугольника ABC делит высоту BH в отношении 25:24, считая от вершины. BC равно 14. Найдите радиус описанной окружности. Ответ: 25.
Оценка эксперта: ____________________
Задание 26.
| Задание |
| Оценка эксперта |
§5. Тренировочные варианты.
Вариант 1.
№1.Решите уравнение 

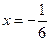
| Баллы | Критерии оценки выполнения задания |
| Правильно выполнены преобразования, получен верный ответ | |
| Решение доведено до конца, но допущена ошибка вычислительного характера или описка, с её учётом дальнейшие шаги выполнены верно | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
№2.Решите уравнение 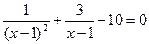
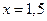
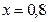
№3.Решите уравнение 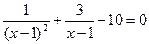
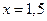
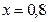
№4. Игорь и Паша могут покрасить забор за 20 часов, Паша и Володя – за 21 час, а Володя и Игорь за 28 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах. Ответ: 900 минут.
| Баллы | Критерии оценки выполнения задания |
| Правильно составлено уравнение, получен верный ответ | |
| Правильно составлено уравнение, но при его решении допущена вычислительная ошибка, с её учётом решение доведено до ответа | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
№5. Игорь и Паша могут покрасить забор за 14 часов, Паша и Володя – за 15 часов, а Володя и Игорь за 30 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах. Ответ: 700 минут.
.
№6. Игорь и Паша могут покрасить забор за 20 часов, Паша и Володя – за 21 час, а Володя и Игорь за 28 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах. Ответ: 900 минут.
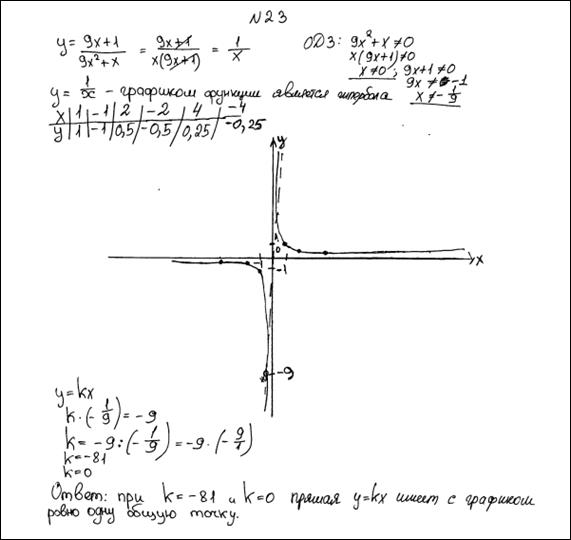
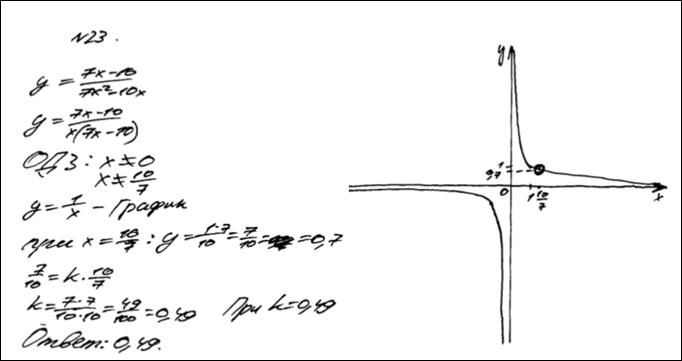
№7. Постройте график функции: 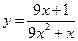
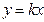
| Баллы | Критерии оценки выполнения задания |
| График построен правильно, верно указаны все значения c , при которых прямая y = c имеет с графиком только одну общую точку | |
| График построен правильно, указаны не все верные значения c | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
№8. Постройте график функции: 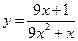
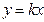
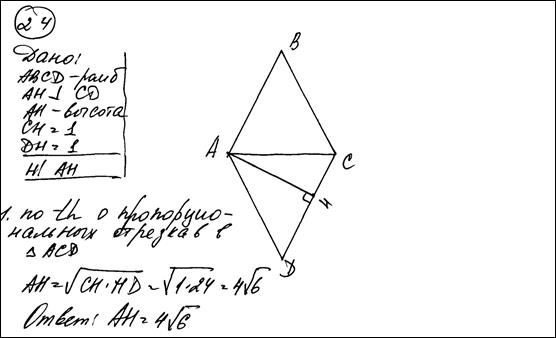
№9. Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба. Ответ: 10.
| Баллы | Критерии оценки выполнения задания |
| Получен верный обоснованный ответ | |
| При верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Оценка эксперта:___________________________________________________ Комментарий:_______________________________________________________________________________________________________________________
№10. Высота, опущенная из вершины ромба, делит противоположную сторону пополам, на отрезки равные 1. Вычислите длину высоты ромба. Ответ: 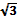
Оценка эксперта:___________________________________________________ Комментарий:_____________________________________________________
№11. Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба. Ответ: 10.
Оценка эксперта:___________________________________________________ Комментарий:_____________________________________________________
№12.Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
| Баллы | Критерии оценки выполнения задания |
| Доказательство верное, все шаги обоснованы | |
| Доказательство в целом верное, но содержит неточности | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Оценка эксперта:___________________________________________________ Комментарий:_____________________________________________________
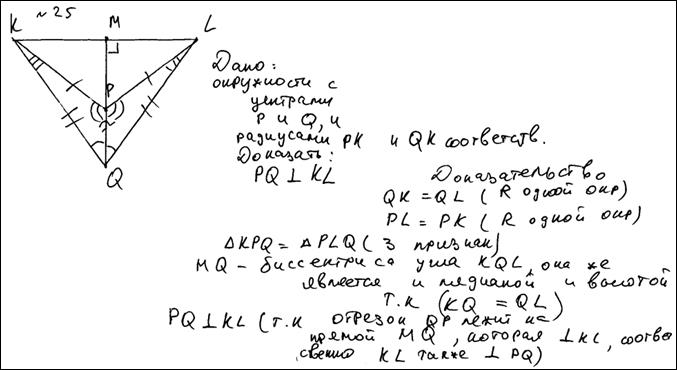
№13.Две окружности с центрами P и Q пересекаются в точках K и L, центры P и Q лежат по одну сторону относительно прямой KL. Докажите, что прямая PQ перпендикулярна прямой KL.
Оценка эксперта:___________________________________________________ Комментарий:_____________________________________________________
№14. Биссектриса угла A, треугольника ABC делит высоту BH в отношении 5:4, считая от вершины. Длина BC равна 6. Найдите радиус описанной окружности.
| Баллы | Критерии оценки выполнения задания |
| Ход решения верный, все его шаги выполнены правильно, получен верный ответ | |
| Ход решения верный, чертёж соответствует условию задачи, но пропущены существенные объяснения или допущена вычислительная ошибка | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Оценка эксперта:___________________________________________________ Комментарий:_____________________________________________________
№15. Биссектриса A, треугольника ABC делит высоту BH в отношении 25:24, считая от вершины. Длина BC равна 14. Найдите радиус описанной окружности.
Оценка эксперта:___________________________________________________ Комментарий:_____________________________________________________
№1.Решите уравнение 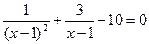
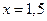
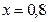
| Баллы | Критерии оценки выполнения задания |
| Правильно выполнены преобразования, получен верный ответ | |
| Решение доведено до конца, но допущена ошибка вычислительного характера или описка, с её учётом дальнейшие шаги выполнены верно | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
№2.Решите уравнение 

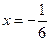
№3.Решите уравнение 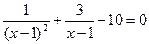
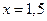
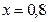
№4.Игорь и Паша могут покрасить забор за 20 часов, Паша и Володя – за 21 час, а Володя и Игорь за 28 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах. Ответ: 900 минут.
| Баллы | Критерии оценки выполнения задания |
| Правильно составлено уравнение, получен верный ответ | |
| Правильно составлено уравнение, но при его решении допущена вычислительная ошибка, с её учётом решение доведено до ответа | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Начало решения задания №4
Продолжение на следующей странице
Продолжение решения задания №4
№5.Игорь и Паша могут покрасить забор за 20 часов, Паша и Володя – за 21 час, а Володя и Игорь за 28 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах. Ответ: 900 минут.
№6.Игорь и Паша могут покрасить забор за 14 часов, Паша и Володя – за 15 часов, а Володя и Игорь за 30 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах. . Ответ: 700 минут.
№7.Постройте график функции: 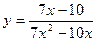
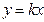
| Баллы | Критерии оценки выполнения задания |
| График построен правильно, верно указаны все значения c , при которых прямая y = c имеет с графиком только одну общую точку | |
| График построен правильно, указаны не все верные значения c | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
№8.Постройте график функции: 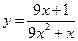
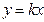
№9.Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба. Ответ: 10.
| Баллы | Критерии оценки выполнения задания |
| Получен верный обоснованный ответ | |
| При верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
№10. Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба. Ответ: 10.
№11.Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба. Ответ: 10.
№12.Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
| Баллы | Критерии оценки выполнения задания |
| Доказательство верное, все шаги обоснованы | |
| Доказательство в целом верное, но содержит неточности | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
№13.Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
№14. Биссектриса A, треугольника ABC делит высоту BH в отношении 25:24, считая от вершины. Длина BC равна 14. Найдите радиус описанной окружности.
| Баллы | Критерии оценки выполнения задания |
| Ход решения верный, все его шаги выполнены правильно, получен верный ответ | |
| Ход решения верный, чертёж соответствует условию задачи, но пропущены существенные объяснения или допущена вычислительная ошибка | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
№15. Биссектриса угла A, треугольника ABC делит высоту BH в отношении 5:4, считая от вершины. Длина BC равна 6. Найдите радиус описанной окружности.
💥 Видео
ЕГЭ 2023 Ященко 7 вариант ФИПИ школе полный разбор!Скачать

№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

ОГЭ без рекламы математика вариант 23 задача 25Скачать

№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Профильный ЕГЭ 2023 математика Ященко. Вариант 8Скачать

ЕГЭ 2023 Ященко 8 вариант ФИПИ школе полный разбор!Скачать

Все задания 25 ОГЭ из банка ФИПИ (математика Школа Пифагора)Скачать

ОГЭ 2022 по математике. Разбор варианта 2 части из ЯщенкоСкачать

#31. Регион ВсОШ 2023, 11.5Скачать

ОГЭ. Математика. Задание 26 | Прямоугольная трапеция и окружность | Борис Трушин |Скачать

ОГЭ-2022 ЗАДАНИЕ-23. ПОЛНЫЙ РАЗБОРСкачать

ОГЭ 2020 Ященко 9 вариант ФИПИ школе полный разбор!Скачать

Алгоритмы. Пересечение окружностейСкачать

Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

ОГЭ 2022 Ященко 25 вариант ФИПИ школе полный разбор!Скачать