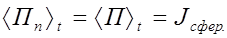| Энергия и импульс электромагнитного поля |   |
Мы уже много раз показывали, что электромагнитное поле обладает энергией. Значит, распространение электромагнитных волн связано с переносом энергии (подобно тому, как распространение упругих волн в веществе связано с переносом механической энергии). Сама возможность обнаружения ЭМВ указывает на то, что они переносят энергию. Для характеристики переносимой волной энергии русским ученым Н.А. Умовым были введены понятия о скорости и направлении движения энергии, о потоке энергии. Спустя десять лет после этого, в 1884 г., английский ученый Джон Пойнтинг описал процесс переноса энергии с помощью вектора плотности потока энергии. Введем вектор Объемная плотность энергии w электромагнитной волны складывается из объемных плотностей Учитывая, что Умножив плотность энергии w на скорость υ распространения волны в среде, получим модуль плотности потока энергии – поток энергии через единичную площадку, перпендикулярную направлению распространения волны в единицу времени:
Так как векторы Вектор плотности потока электромагнитной энергии называется вектором Умова–Пойнтинга:
Вектор В сферической электромагнитной волне, излучаемой ускоренно двигающимися зарядами, векторы Векторы Умова–Пойнтинга зависят от пространства и времени, так как от них зависят модули векторов напряженности электрического и магнитного полей. Поэтому часто пользуются параметром, называемым интенсивностью – модуль среднего значения вектора Умова–Пойнтинга:
Интенсивность пропорциональна квадрату амплитуды:
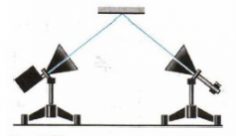
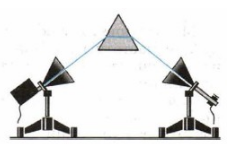
Зависимость интенсивности излучения от направления называют диаграммой направленности. Такая диаграмма для линейного излучателя показана на рис. 6.10. Как доказал Герц, диполь сильнее всего излучает в направлении перпендикулярном по отношению к собственному направлению. Ускоренно двигающиеся заряды излучают электромагнитную энергию в окружающее пространство. Вектор Если электромагнитные волны поглощаются или отражаются телами (эти явления подтверждены опытами Герца), то из теории Максвелла следует, что электромагнитные волны должны оказывать на тела давление. Давление ЭМВ объясняется тем, что под действием электрического поля волны заряженные частицы вещества начинают упорядоченно двигаться и подвергаются со стороны магнитного поля действию силы. Однако, значение этого давления ничтожно мало. Давление света и электромагнитный импульс настолько малы, что непосредственное их измерение затруднительно. Так, зеркало, расположенное на расстоянии 1 м от источника света в миллион свечей (кандел), испытывает давление 10 — 7 Н/м 2 . Давление излучения Солнца на поверхность Земли равно 4,3×10 — 6 Н/м 2 , а общее давление излучения Солнца на Землю равно 6×10 8 Н, что в 10 13 раз меньше силы притяжения Солнца. Световое давление было впервые обнаружено и измерено в 1899 г. в Москве русским ученым П.Н. Лебедевым (1866-1912). Его результаты, как и более точные измерения последующих исследователей, согласуются с теорией в пределах ошибок опыта — до 2 %. На рис. 6.11 изображен прибор, с помощью которого было измерено давление света, – радиометр. Свет, отраженный посеребренной поверхностью каждой лопасти 2, 3, передает вдвое больший импульс по сравнению со светом, поглощенным зачерненной поверхностью 1, 4. Вследствие этого лопасти начинают вращаться по часовой стрелке. Давление света можно рассчитать по формуле: где J – интенсивность света, K – коэффициент отражения. Опыты Лебедева имели огромное значение для утверждения выводов теории Максвелла о том, что свет представляет собой ЭМВ. Давление света играет существенную роль в двух противоположных по масштабу областях явлений. Так, например, гравитационное притяжение верхних слоев звезд к центру в значительной мере уравновешивается силой давления светового потока, идущего от центра звезды наружу. В атомных процессах существенной является отдача, испытываемая возбужденным атомом при излучении им света в силу малости массы атома. Световое давление может создавать ускорение атомов до Впервые гипотеза о световом давлении была высказана в 1619 г. немецким ученым И. Кеплером (1571-1630) для объяснения отклонения хвостов комет, пролетающих вблизи Солнца (рис. 6.12). Возможными областями физического применения светового давления могут служить процессы разделения смеси изотопов газов, ускорение микрочастиц и создание условий для протекания управляемой термоядерной реакции. Электромагнитная масса и импульс Существование давления ЭМВ приводит к выводу о том, что электромагнитному полю присущ механический импульс. Выражая импульс как
Это соотношение между массой и энергией ЭМП является универсальным законом природы, справедливым для любых тел независимо от их внутреннего строения. Импульс электромагнитного поля, связанного с движущейся частицей, – электромагнитный импульс – оказался пропорциональным скорости частицы υ, что имеет место и в выражении для обычного импульса mυ, где m – инертная масса заряженной частицы. Поэтому коэффициент пропорциональности в полученном выражении для импульса
где е – заряд движущейся частицы, а – ее радиус. И даже если тело не обладает никакой иной массой, оказывается, что между импульсом и скоростью заряженной частицы существует соотношение:
Это соотношение как бы раскрывает происхождение массы – это электродинамический эффект. Движение заряженной частицы сопровождается возникновением магнитного поля. Магнитное поле сообщает телу дополнительную инертность – при ускорении затрачивается работа на создание магнитного поля, при торможении –работа против затормаживающих сил индукционного происхождения. По отношению к движущемуся заряду электромагнитное поле является средой, неотделимой от заряда. В общем случае можно записать, что полный импульс равен сумме механического и электромагнитного импульсов; возможно, что другие поля вносят и иные вклады в полную массу частицы, но, определенно, в полной массе есть электромагнитная часть: Если учесть релятивистские эффекты сокращения длины и преобразования электрических и магнитных полей, то для электромагнитного импульса получается также релятивистски инвариантная формула:
Таким же образом изменяется релятивистский механический импульс. Содержание
Видео:Билет №38 "Поток энергии"Скачать  Подставляя (2.4.3) в (2.4.2) и учитывая (2.4.4), получимУчтем, что энергия волны переносится в направление скорости ее распространения, тогда (2.4.5) можно записать в векторном виде. Выражение для вектора Найдем выражение для вектора плотности потока энергии, переносимой электромагнитной волной. Объемная плотность энергии в электромагнитной волне состоит из двух вкладов — от электрического и магнитного полей: Векторы Из (2.4.8) и (2.4.7) следует, что объемная плотность энергии электрического и магнитных полей в электромагнитной волне в каждый момент времени одинакова, то есть Электромагнитная волна распространяется в среде со скоростью Подставим в формулу (2.4.5) выражения для w и V, тогда получим П=Е Н. (2.4.10) С учетом взаимной ориентации векторов Выражение (2.4.11) было получено Пойнтингом, поэтому вектор В электромагнитной волне векторы n = (0.75¸0.4)10 15 Гц. За столь частыми изменениями энергии не сможет уследить ни один приемник, вследствие чего будет регистрироваться усредненное по времени значение модуля вектора плотности потока энергии, которое называется интенсивностью волны: Получим выражения для интенсивности плоской и сферической электромагнитной волны. Уравнения плоской и сферической электромагнитных волн, распространяющихся в произвольном направлении, имеют вид (2.2.14, 2.2.19, 2.2.20): Подставляя модули векторов Подстановка Для нахождения интенсивности волн (2.4.13) и (2.4.14) необходимо найти средние за период значения от выражений (2.4.15) и (2.4.16). Учтем, что тогда для интенсивностей волн получим Зависимость амплитуды сферической волны от r в уравнениях (2.2.14), (2.4.14) связана с тем, что если среда не поглощает энергию волны, то средний поток энергии, проходящий через сферу любого радиуса, должен быть одинаков. Действительно, из (2.4.2) находим поток энергии через площадку D DФ=ПD Для нахождения потока энергии через замкнутую поверхность S необходимо вычислить интеграл где Пn — нормальная составляющая вектора
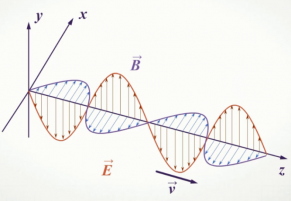
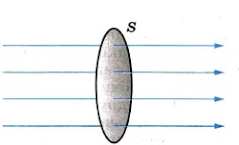
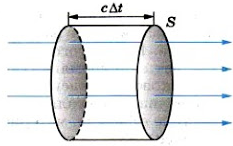
Усредненный по времени поток энергии переносимой сферической волной через сферу произвольного радиуса найдем согласно (2.4.20) по формуле Направления распространения сферической волны и нормали к любому элементу сферической поверхности совпадают, поэтому Воспользовавшись выражением (2.4.17) для Jсфер из (2.4.21) получим Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать  Электромагнитные волнытеория по физике 🧲 колебания и волныВспомним, что волна — это колебания, распространяющиеся в пространстве. Механическая волна представляет собой колебания, распространяющиеся в вещественной среде. Тогда электромагнитная волна — это электромагнитные колебания, которые распространяются в электромагнитном поле. Видео:Вектор Умова-Пойнтинга ● 1Скачать  Как появляются и распространяются электромагнитные волныПредставьте себе неподвижный точечный заряд. Пусть его окружают еще много таких зарядов. Тогда он будет действовать на них с некоторой кулоновской силой (и они на него). А теперь представьте, что заряд сместился. Это приведет к изменению расстояния по отношению к другим зарядам, а, следовательно, и к изменению сил, действующих на них. В результате они тоже сместятся, но с некоторым запаздыванием. При этом начнут смещаться и другие заряды, которые взаимодействовали с ними. Так распространяется электромагнитные взаимодействия. Теперь представьте, что заряд не просто сместился, а он начал быстро колебаться вдоль одной прямой. Тогда по характеру движения он будет напоминать шарик, подвешенный к пружине. Разница будет только в том, что колебания заряженных частиц происходят с очень высокой частотой. Вокруг колеблющегося заряда начнет периодически изменяться электрическое поле. Очевидно, что период изменений этого поля, будет равен периоду колебаний заряда. Периодически меняющееся электрическое поле будет порождать периодически меняющееся магнитное поле. Это магнитное поле, в свою очередь, будет создавать переменное электрическое поле, но уже на большем расстояние от заряда, и т.д. В результате появления взаимно порождаемых полей в пространстве, окружающем заряд, возникает система взаимно перпендикулярных, периодически меняющихся электрических и магнитных полей. Так образуется электромагнитная волна, которая распространяется от колеблющегося заряда во все стороны. Электромагнитная волна не похожа на те возмущения вещественной среды, которые вызывают механические волны. Посмотрите на рисунок. На нем изображены векторы напряженности → E и магнитной индукции → B в различных точках пространства, лежащих на оси Oz, в фиксированный момент времени. Никаких гребней и впадин среды при этом не появляется. В каждой точке пространства электрические и магнитные пол меняются во времени периодически. Чем дальше расположена точка от заряда, тем позднее ее достигнут колебания полей. Следовательно, на разных расстояниях от заряда колебания происходят с различными фазами. Колебания векторов → E и → B в любой точке совпадают по фазе. Длина электромагнитной волны — расстояние между двумя ближайшими точками, в которых колебания происходят в одинаковых фазах. Длина электромагнитной волны обозначается как λ. Единица измерения — м (метр). Обратите внимание на рисунок выше. Векторы магнитной индукции и напряженности поля, являющиеся периодически изменяющимися величинами, в любой момент времени перпендикулярны направлению распространения волны. Следовательно, электромагнитная волна — поперечная волна. Видео:44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать  Условия возникновения электромагнитных волнЭлектромагнитные волны излучаются только колеблющимися заряженными частицами. При этом важно, чтобы скорость их движения постоянно менялась, т.е. чтобы они двигались с ускорением. Наличие ускорения — главное условие возникновения электромагнитных волн. Электромагнитное поле может излучаться не только колеблющимся зарядом, но и заряженной частицей, перемещающейся с постоянно меняющейся скоростью. Интенсивность электромагнитного излучения тем больше, чем больше ускорение, с которым движется заряд. Представим заряд, движущийся с постоянной скоростью. Тогда создаваемые им электрическое и магнитное поля будут сопровождать его как шлейф. Только при ускорении заряда поля «отрываются» от частицы и начинают самостоятельное существование в форме электромагнитных волн. Впервые существование электромагнитных волн предположил Максвелл, который посчитал, что они должны распространяться со скоростью света. Но экспериментально они были обнаружены лишь спустя 10 лет после смерти ученого. Их открыл Герц. Он же подтвердил, что скорость распространения электромагнитных волн равна скорости света: c = 300 000 км/с. Видео:Урок 222. Поток вектора напряженности электрического поляСкачать  Плотность потока электромагнитного излученияИзлученные электромагнитные волны несут с собой энергию. Рассмотрим поверхность площадью S, через которую электромагнитные волны переносят энергию. На рисунке выше прямые линии указывают направления распространения электромагнитных волн. Это лучи — линии, перпендикулярные поверхностям, во всех точках которых колебания происходят в одинаковых фазах. Такие поверхности называются волновыми поверхностями. Плотность потока электромагнитного излучения, или интенсивность волны — отношение электромагнитной энергии ΔW, проходящей за время Δt через перпендикулярную лучам поверхность площадью S, к произведению площади S на время Δt. Плотность потока электромагнитного излучения обозначается как I. Единица измерения — Вт/м 2 (ватт на квадратный метр). Поэтому плотность потока электромагнитного излучения фактически представляет собой мощность электромагнитного излучения, проходящего через единицу площади поверхности. Численно плотность потока электромагнитного излучения определяется формулой: Выразим I через плотность электромагнитной энергии и скорость ее распространения с. Выберем поверхность площадью S, перпендикулярную лучам, и построим на ней как на основании цилиндр с образующей cΔt (см. рисунок ниже). Объем цилиндра: ΔV = ScΔt. Энергия электромагнитного поля внутри цилиндра равна произведению плотности энергии на объем: ΔW = w cΔtS. Вся эта энергия за время Δt пройдет через правое основание цилиндра. Поэтому получаем: I = w c Δ t S S Δ t . . = w c Следовательно, плотность потока электромагнитного излучения равна произведению плотности электромагнитной энергии на скорость ее распространения. Плотность электромагнитной энергии — энергия электромагнитного излучения в единице объема. Обозначается как w. Единица измерения — Дж/м 3 . Пример №1. Плотность потока излучения равна 6 мВт/м 2 . Найти плотность энергии электромагнитной волны. w = I c . . = 6 · 10 − 3 3 · 10 8 . . = 2 · 10 − 11 ( Д ж м 3 . . ) Точечный источник излученияИсточники излучения электромагнитных волн могут быть весьма разнообразными. Простейшим является точечный источник. Точечный источник — источник излучения, размеры которого много меньше расстояния, на котором оценивается его действие. Предполагается, что точечный источник посылает электромагнитные волны по всем направлениям с одинаковой интенсивностью. В действительности таких источников не существует. Но за такие источники излучения можно принять звезды, так как расстояние между ними существенно больше размеров самих звезд. Энергия, которую переносят электромагнитные волны, с течением времени распределяется по все большей и большей поверхности. Поэтому энергия, передаваемая через поверхность единичной площадки за единицу времени, т. е. плотность потока излучения, уменьшается по мере удаления от источника. Поместим точечный источник в центр сферы радиусом R. Площадь поверхности сферы S = 4πR 2 . Если считать, что источник по всем направлениям за время Δt излучает суммарную энергию ΔW, получим: I = Δ W S Δ t . . = Δ W 4 π Δ t . . · 1 R 2 . . Плотность потока излучения от точечного источника убывает обратно пропорционально квадрату расстояния до источника. Пример №2. Плотность потока электромагнитного излучения на расстоянии 5 метров от точечного источника составляет 20 мВт/м 2 . Найти плотность потока электромагнитного излучения на расстоянии 10 метров от этого источника. Расстояние по условию задачи увеличилось вдвое. Так как плотность потока излучения от точечного источника убывает обратно пропорционально квадрату расстояния до источника, при увеличении расстояния вдвое интенсивность излучения уменьшится в 4 раза. То есть, она станет равной 5 мВт/м 2 . Зависимость плотности потока излучения от частотыНапряженность электрического поля и магнитная индукция электромагнитной волны пропорциональны ускорению заряда. Ускорение при гармонических колебаниях пропорционально квадрату частоты. Поэтому напряженность электрического поля и магнитная индукция также пропорциональны квадрату частоты: Плотность энергии электрического поля пропорциональна квадрату напряженности поля. Энергия магнитного поля, как это можно показать, пропорциональна квадрату магнитной индукции. Полная плотность энергии электромагнитного поля равна сумме плотностей энергий электрического и магнитного полей. Поэтому плотность потока излучения I пропорциональна: Плотность потока излучения пропорциональна четвертой степени частоты. Так, при увеличении частоты колебаний зарядов в 2 раза энергия, излучаемая ими, возрастает в 16 раз. При увеличении частоты в 3 раза, энергия излучения увеличивается в 81 раз, и т.д. Пример №3. Частота электромагнитной волны уменьшилась в 4 раза. Найти, во сколько раз изменилась плотность потока излучения. Так как плотность потока излучения пропорциональна четвертой степени частоты, мы можем найти плотность потока излучения путем извлечения корня из числа 4 дважды: 4 √ 4 = √ √ 4 = √ 2 ≈ 1 , 4 Плотность потока излучения уменьшилась в 1,4 раза. Видео:Вектор Умова-Пойнтинга ● 5Скачать  Свойства электромагнитных волнСовременные радиотехнические устройства позволяют провести очень наглядные опыты по наблюдению свойств электромагнитных волн. При этом лучше всего пользоваться волнами сантиметрового диапазона. Эти волны излучаются специальным генератором сверхвысокой частоты (СВЧ). Электрические колебания генератора модулируют звуковой частотой. Принятый сигнал после детектирования подается на громкоговоритель.
Видео:Билет №02 "Теорема Гаусса"Скачать  Шкала электромагнитных волнЭлектромагнитные волны имеют большое разнообразие. Они классифицируются по длине волны λ или связанной с ней частоте ν. Шкала электромагнитных волн включает в себя:
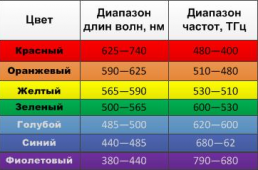
Укажем частоты и длины указанных волн, а также их подробную классификацию в таблице.
Частоты и длины волн электромагнитного излучения видимого спектра смотрите на рисунке ниже. В электромагнитной волне, распространяющейся со скоростью → v , происходят колебания векторов напряжённости электрического поля → E и индукции магнитного поля → B . При этих колебаниях векторы → v , → E , → B . имеют взаимную ориентацию: 🔍 ВидеоУрок 225. Задачи на поток вектора напряженности электрического поляСкачать  45. Электрическое смещениеСкачать  Вектор Умова-Пойнтинга ● 4Скачать  Поток вектора напряженности электрического поля. Теорема Гаусса. Практическая часть. 10 класс.Скачать  4.8 Плотность потока мощности электромагнитной волныСкачать  Вектор Умова-Пойнтинга ● 3Скачать  Билет №16 "Теорема о циркуляции и теорема Гаусса для магнитного поля"Скачать  Вектор Умова-Пойнтинга ● 2Скачать  Экспериментальное обнаружение электромагнитных волн | Физика 11 класс #20 | ИнфоурокСкачать  Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать  Урок 281. Электромагнитная индукция. Магнитный поток. Правило ЛенцаСкачать  Поток вектора магнитной индукцииСкачать  Урок 384. Излучение электромагнитных волн.Скачать  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 — приращение плотности электромагнитной энергии, где сама величина w определяется интегралом:
— приращение плотности электромагнитной энергии, где сама величина w определяется интегралом: .
. и
и  электрического и магнитного полей:
электрического и магнитного полей: .
. , получим, что плотность энергии электрического и магнитного полей в каждый момент времени одинакова, т.е.
, получим, что плотность энергии электрического и магнитного полей в каждый момент времени одинакова, т.е.  . Поэтому
. Поэтому .
. .
. и
и  взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора [
взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора [  ] совпадает с направлением переноса энергии, а модуль этого вектора равен EH (рис. 6.8).
] совпадает с направлением переноса энергии, а модуль этого вектора равен EH (рис. 6.8).
 .
.
 направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.
направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны. (рис. 6.9).
(рис. 6.9).
 .
. .
.
 и убывает обратно пропорционально r 2 . Излучение максимально в направлении, перпендикулярном вектору
и убывает обратно пропорционально r 2 . Излучение максимально в направлении, перпендикулярном вектору  , и отсутствует вдоль этого вектора. Поэтому диаграмма направленности диполя имеет вид двух симметричных лепестков, как показано на рис. 6.10.
, и отсутствует вдоль этого вектора. Поэтому диаграмма направленности диполя имеет вид двух симметричных лепестков, как показано на рис. 6.10.

 ,
, , где g – ускорение свободного падения.
, где g – ускорение свободного падения.

 (поле в вакууме распространяется со скоростью света с), получим
(поле в вакууме распространяется со скоростью света с), получим ,
, .
. называют электромагнитной массой:
называют электромагнитной массой: ,
, .
. ,
,  .
. .
.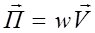 . (2.4.6)
. (2.4.6)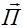 , впервые было получено русским ученым Н.А.Умовымдля упругих волн. Поэтому вектор
, впервые было получено русским ученым Н.А.Умовымдля упругих волн. Поэтому вектор 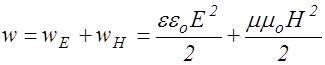 . (2.4.7)
. (2.4.7)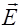 и
и  в электромагнитной волне изменяются в фазе (§ 2.3), поэтому выражение (2.4.7) справедливо не только для амплитудных значений [формула (2.3.43)], но и для мгновенных, причем
в электромагнитной волне изменяются в фазе (§ 2.3), поэтому выражение (2.4.7) справедливо не только для амплитудных значений [формула (2.3.43)], но и для мгновенных, причем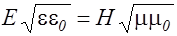 . (2.4.8)
. (2.4.8)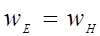 , поэтому справедливо:
, поэтому справедливо: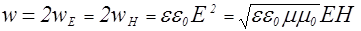 . (2.4.9)
. (2.4.9)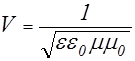 .
.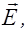
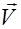 (рис.2.3.3), вектор плотности потока энергии можно записать в виде
(рис.2.3.3), вектор плотности потока энергии можно записать в виде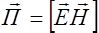 . (2.4.11)
. (2.4.11)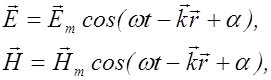 (2.4.13)
(2.4.13)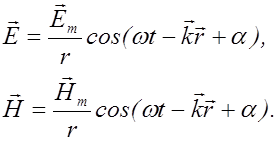 (2.4.14)
(2.4.14)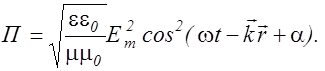 (2.4.15)
(2.4.15)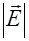 и
и 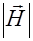 из (2.4.14) в (2.4.10) дает для плотности потока энергии в сферической волне выражение
из (2.4.14) в (2.4.10) дает для плотности потока энергии в сферической волне выражение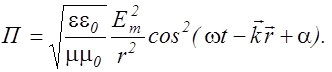 (2.4.16)
(2.4.16)
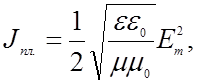 (2.4.17)
(2.4.17)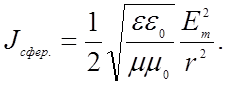 (2.4.18)
(2.4.18)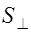 , расположенную перпендикулярно к направлению распространения волны:
, расположенную перпендикулярно к направлению распространения волны: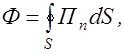 (2.4.20)
(2.4.20)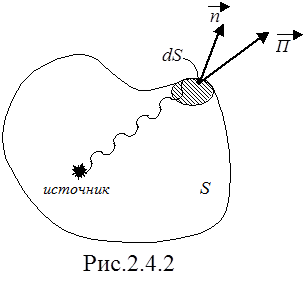
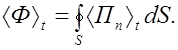 (2.4.21)
(2.4.21)