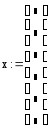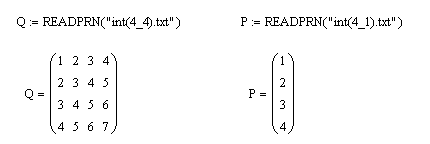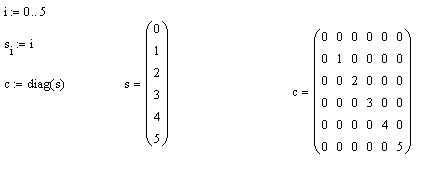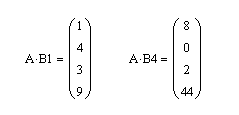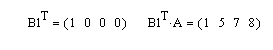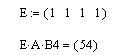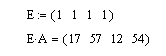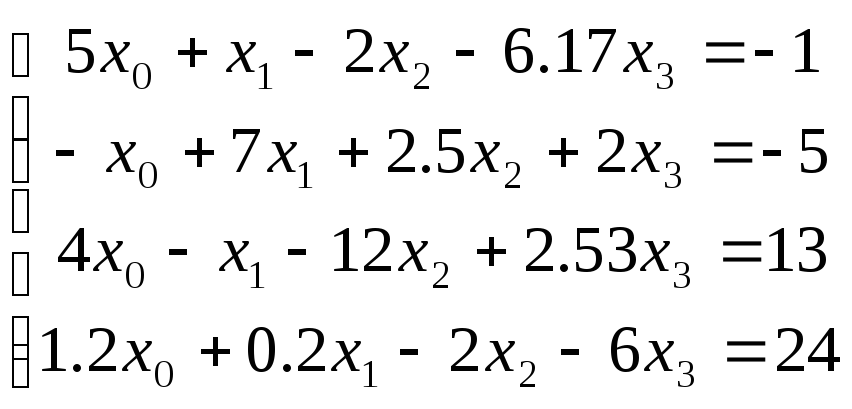Mathcad содержит функции для обычных в линейной алгебре действий с массивами. Эти функции предназначены для использования с векторами и матрицами. Если явно не указано, что функция определена для векторного или матричного аргумента, не следует в ней использовать массивы как аргумент. Обратите внимание, что операторы, которые ожидают в качестве аргумента вектор, всегда ожидают вектор-столбец, а не вектор-строку. Чтобы заменить вектор-строку на вектор-столбец, используйте оператор транспонирования [Ctrl]1.
Если Вы используете Mathcad PLUS, Вы будете также иметь несколько дополнительных функций, определенных для векторов. Эти функции скорее предназначены для анализа данных, чем для действий с матрицами. Они обсуждены в Главе “Встроенные функции”.
Следующие таблицы перечисляют векторные и матричные функции Mathcad. В этих таблицах
- A и B — массивы (векторы или матрицы).
- v — вектор.
- M и N — квадратные матрицы.
- z — скалярное выражение.
- Имена, начинающиеся с букв m, n, i или j — целые числа.
Размеры и диапазон значений массива
В Mathcad есть несколько функций, которые возвращают информацию относительно размеров массива и диапазона его элементов. Рисунок 10 показывает, как эти функции используются.
| Имя функции | Возвращается. |
| rows(A) | Число строк в массиве A. Если А — скаляр, возвращается 0. |
| cols(A) | Число столбцов в массиве A. Если A скаляр, возвращается 0. |
| length(v) | Число элементов в векторе v. |
| last(v) | Индекс последнего элемента в векторе v. |
| max(A) | Самый большой элемент в массиве A. Если A имеет комплексные элементы, возвращает наибольшую вещественную часть плюс i, умноженную на наибольшую мнимую часть. |
| min(A) | Самый маленький элемент в массиве A. Если A имеет комплексные элементы, возвращает наименьшую вещественную часть плюс i, умноженную на наименьшую мнимую часть. |
Рисунок 10: Векторные и матричные функции для нахождения размера массива и получения информации относительно диапазона элементов.
Специальные типы матриц
Можно использовать следующие функции, чтобы произвести от массива или скаляра матрицу специального типа или формы. Функции rref, diag и geninv доступны только в Mathcad PLUS.
| Имя функции | Возвращается. |
| identity(n) | n x n единичная матрица (матрица, все диагональные элементы которой равны 1, а все остальные элементы равны 0). |
| Re(A) | Массив, состоящий из элементов, которые являются вещественными частями элементов A. |
| Im(A) | Массив, состоящий из элементов, которые являются мнимыми частями элементов A. |
| Е diag(v) | Диагональная матрица, содержащая на диагонали элементы v. |
| Е geninv(A) | Левая обратная к A матрица L такая, что L A = I, где I — единичная матрица, имеющая то же самое число столбцов, что и A. Матрица А — m x n вещественная матрица, где m>=n. A = I, где I — единичная матрица, имеющая то же самое число столбцов, что и A. Матрица А — m x n вещественная матрица, где m>=n. |
| Е rref(A) | Ступенчатая форма матрицы A. |
Рисунок 11: Функции для преобразования массивов. Обратите внимание, что функции diag и rref являются доступными только в Mathcad PLUS.
Специальные характеристики матрицы
Можно использовать функции из следующей таблицы, чтобы найти след, ранг, нормы и числа обусловленности матрицы. Кроме tr, все эти функции доступны только в Mathcad PLUS.
| Имя функции | Возвращается. |
| tr(M) | Сумма диагональных элементов, называемая следом M. |
| Е rank(A) | Ранг вещественной матрицы A. |
| Е norm1(M) | L1 норма матрицы M. |
| Е norm2(M) | L2 норма матрицы M. |
| Е norme(M) | Евклидова норма матрицы M. |
| Е normi(M) | Равномерная норма матрицы M. |
| Е cond1(M) | Число обусловленности матрицы M, основанное на L1 норме. |
| Е cond2(M) | Число обусловленности матрицы M, основанное на L2 норме. |
| Е conde(M) | Число обусловленности матрицы M, основанное на евклидовой норме. |
| Е condi (M) | Число обусловленности матрицы M, основанное на равномерной норме. |
Формирование новых матриц из существующих
В Mathcad есть две функции для объединения матриц вместе — бок о бок, или одна над другой. В Mathcad также есть функция для извлечения подматрицы. Рисунки 12 и 13 показывают некоторые примеры.
| Имя функции | Возвращается. |
| augment (A, B) | Массив, сформированный расположением A и B бок о бок. Массивы A и B должны иметь одинаковое число строк. |
| stack (A, B) | Массив, сформированный расположением A над B. Массивы A и B должны иметь одинаковое число столбцов. |
| submatrix (A, ir, jr, ic, jc) | Субматрица, состоящая из всех элементов, содержащихся в строках с ir по jc и столбцах с ic по jc. Чтобы поддерживать порядок строк и-или столбцов, удостоверьтесь, что ir |
Рисунок 12: Объединение матриц функциями stack и augment.
Рисунок 13: Извлечение субматрицы из матрицы при помощи функции submatrix.
Собственные значения и собственные векторы
В Mathcad существуют функции eigenval и eigenvec для нахождения собственных значений и собственных векторов матрицы. В Mathcad PLUS также есть функция eigenvecs для получения всех собственных векторов сразу. Если Вы используете Mathcad PLUS, Вы будете также иметь доступ к genvals и genvecs для нахождения обобщенных собственных значений и собственных векторов. Рисунок 14 показывает, как некоторые из этих функций используются.
| Имя функции | |
| eigenvals (M) | Вектор, содержащий собственные значения матрицы M. |
| eigenvec (M, z) | Матрица, содержащая нормированный собственный вектор, соответствующий собственному значению z квадратной матрицы M. |
| Е eigenvecs (M) | Матрица, содержащая нормированные собственные векторы, соответствующие собственным значениям квадратной матрицы M. n-ный столбец возвращенной матрицы — собственный вектор, соответствующий n-ному собственному значению, возвращенному eigenvals. |
| Е genvals (M,N) | Вектор v собственных значений, каждое из которых удовлетворяет обобщенной задаче о собственных значениях . Матрицы M и N — вещественнозначные квадратные матрицы одного размера. Вектор x — соответствующий собственный вектор. |
| Е genvecs (M,N) | Матрица, содержащая нормализованные собственные векторы, соответствующие собственным значениям в v, векторе, возвращенном genvals. n-ный столбец этой матрицы — собственный вектор x, удовлетворяющий обобщенной задаче о собственных значениях . Матрицы M и N — вещественнозначные квадратные матрицы одного размера. |
Рисунок 14: Нахождение собственных значений и собственных векторов.
Рисунок 15: Использование eigenvecs для одновременного нахождения всех собственных векторов.
Если Вы используете Mathcad PLUS, Вы будете иметь доступ к некоторым дополнительным функциям для выполнения специальных разложений матрицы: QR, LU, Холесского, и по сингулярным базисам. Некоторые из этих функций возвращают две или три матрицы, соединенные вместе в одну большую матрицу. Используйте submatrix, чтобы извлечь эти две или три меньшие матрицы. Рисунок 16 показывает пример.
| Имя функции | Возвращается. |
| Е cholesky(M) | Нижняя треугольная матрица L такая, что L L T =M. Матрица M должна быть симметричной положительно определенной. Симметрия означает, что M=M T , положительная определённость — что x T L T =M. Матрица M должна быть симметричной положительно определенной. Симметрия означает, что M=M T , положительная определённость — что x T  M M x>0 для любого вектора x x>0 для любого вектора x  0. 0. |
| Е qr(A) | Матрица, чьи первые n столбцов содержат ортогональную матрицу Q, а последующие столбцы содержат верхнюю треугольную матрицу R. Матрицы Q и R удовлетворяют равенству A=Q R. Матрица A должна быть вещественной. R. Матрица A должна быть вещественной. |
| Е lu(M) | Матрица, которая содержит три квадратные матрицы P, L и U, расположенные последовательно в указанном порядке и имеющие с M одинаковый размер. L и U являются соответственно нижней и верхней треугольными матрицами. Эти три матрицы удовлетворяют равенству P M=L M=L U . U . |
| Е svd(A) | Матрица, содержащая две расположенные друг над другом матрицы U и V. Сверху находится U — размера m x n, снизу V — размера n x n. Матрицы U и V удовлетворяют равенству A=U diag(s) diag(s) V T , где s — вектор, возвращенный svds(A). A должна быть вещественнозначной матрицей размера m x n, где m>=n. V T , где s — вектор, возвращенный svds(A). A должна быть вещественнозначной матрицей размера m x n, где m>=n. |
| Е svds(A) | Вектор, содержащий сингулярные значения вещественнозначной матрицы размера m x n, где m>=n. |
Рисунок 16: Использование функции submatrix для извлечения результата из функции rq. Используйте submatrix, чтобы извлечь подобным образом результаты из функций lu и svd. Обратите внимание, что эти функции доступны только в Mathcad PLUS.
Решение линейной системы уравнений
Если Вы используете Mathcad PLUS, Вы сможете использовать функцию lsolve для решения линейной системы уравнений. Рисунок 17 показывает пример. Обратите внимание, что M не может быть ни вырожденной, ни почти вырожденной для использования с lsolve. Матрица называется вырожденной, если её детерминант равен нулю. Матрица почти вырождена, если у неё большое число обусловленности. Можно использовать одну из функций, описанных на странице 204, чтобы найти число обусловленности матрицы.
| Имя функции | |
| Е lsolve (M, v) | Вектор решения x такой, что M x=v. x=v. |
Если Вы не используете Mathcad PLUS, Вы всё-таки можете решать систему линейных уравнений, используя обращение матрицы, как показано в нижнем правом углу Рисунка 9.
Рисунок 17: Использование lsolve для решения системы из двух уравнений с двумя неизвестными.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
- Лекція№9 — Операции с векторами и матрицами, матричные функции в математическом пакете MathCad
- 3.1. Создание векторов и матриц
- 3.2. Использование матриц специального вида для выполнения матричных операций в системе MathCad
- 3.3. Решение систем линейных алгебраических уравнений с использованием матричных преобразований
- MathCAD — это просто! Часть 10. Работа с векторами и матрицами
- 🌟 Видео
Видео:Матрицы в Mathcad(создание и редактирование матриц)(Урок 3.1)Скачать
Лекція№9 — Операции с векторами и матрицами, матричные функции в математическом пакете MathCad
Матричное исчисление играет важную роль в компьютерной математике. Практически все численные методы на том или ином этапе работы своего алгоритма сводятся к решению систем линейных алгебраических уравнений (СЛАУ), которое часто производится матричными методами. Вообще говоря, нельзя назвать ни одной области использования компьютера, в алгоритмах которой (в большей или меньшей степени) не использовались бы матрицы.
Понятие «вектор» обычно не отделяют от понятия «матриц». Векторы могут рассматриваться как матрицы, состоящие из одного столбца (или строки).
Матричные вычисления в MathCAD можно условно разделить на три основных типа.
К первому относятся такие элементарные действия над матрицами, как создание, извлечение из них данных, их умножение, сложение или скалярное произведение (в случае векторов). Для их реализации служат специальные операторы трех панелей семейства Math (Математические): Calculator (Калькулятор), Matrix (Матричные) иSymbolics (Символьные).
Ко второму типу можно отнести те матричные преобразования, которые требуют использования специальных функций и встроенных алгоритмов матричной алгебры, таких как, например, функции вычисления определителя, матричных норм или сортировки элементов векторов по возрастанию. Функции этой группы можно найти в категории Vector and Matrix (Векторные и матричные) у мастера функций.
И, наконец, к третьему типу матричных вычислений следует отнести те задачи, решить которые можно только используя возможности системы программирования MathCAD.
В языках программирования начальные индексы массивов обычно равняются 0. По умолчанию в MathCAD индексы строк и столбцов также отсчитываются с 0. В том случае, если такая система вам неудобна или непривычна, можно изменить точку отсчета индексов на 1, задав системную переменную ORIGIN: ORIGIN:= 1.
Доступ к элементам вектора или матрицы осуществляется с помощью индексированных переменных. Например, чтобы использовать пятый элемент вектора с именем А, нужно записать этот элемент в виде: 

Для задания индексов на панели Matrix предусмотрена специальная кнопка Subscript (Индекс). Перейти к записи индекса можно также с помощью клавиши «[» ( левая квадратная скобка). Нажав ее, вы увидите, что на месте будущего индекса, чуть ниже текста имени матрицы, появится черный маркер. В него через запятую следует ввести значения индексов. На первом месте при этом должен стоять номер строки, а на втором – столбца.
Видео:7. MathCad. Векторы и матрицыСкачать

3.1. Создание векторов и матриц
В системе предусмотрены различные возможности задания векторов и матриц:
Определение матрицы последовательным заданием каждого элемента.
С помощью индексированных переменных.
С помощью использования команды Insert→Matrix, либо с помощью соответствующей кнопки панели Matrix.
Задание с помощью элементов программирования.
Применение встроенных функций.
Через связь с другим приложением, например Excel.
Создание таблицы данных.
Чтение из внешнего файла.
Рассмотрим некоторые из них. Определение матрицы последовательным заданием каждого элемента очевидно и не требует пояснений. При создании матрицы или вектора с помощью индексированной переменной следует исходить из того, что любая индексированная переменная, индексами которой являются переменные, принимающие целочисленные значения из некоторого промежутка, уже представляют собой вектор или матрицу.
Пример 1. Требуется сформировать вектор x, состоящий из 6 элементов. Элементам этого вектора присвоить значения индексов.
Решение. Предоставим два варианта решения этой задачи:
с помощью индексированной переменной;
с помощью команды Insert→Matrix.
Вариант а
Для того, чтобы сформировать вектор, воспользуемся вспомогательной переменной, которая будет играть роль индекса (например, i), а затем будем использовать эту переменную для здания элементных значений вектора x. Формирование вектора представлено на рис. 3.1.
Рис. 3.1. Формирование вектора с использованием индексированной переменной
Вариант b
Формирование вектора х будем производить с помощью команды Matrix. Для этого сначала напишем оператор присваивания: «х:=» , а затем выполним команду Matrix. Эта команда открывает диалоговое окно«Insert Matrix», которое представлено на рис. 3.2, в котором необходимо указать число строк и число столбцов. В нашем примере число строк равно 6, а число столбцов равно 1.
После нажатия кнопки «Ok» команда предоставит шаблон с шестью ячейками, в которые следует вписать значения элементов вектора.
Рис. 3.2. Вызов диалогового окна «Insert Matrix» для создания матрицы с помощью команды «Matrix»
Пример 2. В файле с именем «int(4_4).txt» записаны числа в виде матрицы четыре строчки по четыре элемента, разделенными пробелами. В файле с именем «int(4_1).txt» записаны числа в столбик. Требуется прочитать эти данные в матрицу Q и вектор P.
Решение. Для чтения данных из файла в матрицу/вектор можно воспользоваться функцией READPRN, которая имеет один параметр — имя файла. Фрагмент с решением представлен на рис. 3.3.
Рис. 3.3. Чтение данных из файлов
С матрицами могут производиться как численные, так и символьные вычисления. Операции с матрицами в системе MathCAD обозначаются так, как это принято в математике: —, +, *, … .
На рис. 3.4 показано назначение некоторых специализированных команд, расположенных на панели инструментов Matrix.
Помимо этого, система MathCAD представляет большое количество функций для работы с векторами и матрицами. Воспользоваться этими функциями можно с помощью мастера функций f(x).
Х -1 – получить обратную матрицу
|X| – вычислить детерминант
М Т – транспонировать
М – из матрицы взять вектор-столбец
v – получить сумму элементов

Рис. 3.4. Назначение некоторых команд, расположенных на панели инструментов «Matrix»
На рис. 3.5 представлены вычисления с использованием операций над матрицами.
Рис. 3.5. Примеры матричных вычислений в MathCAD
Пример 3. Требуется сформировать диагональную квадратную матрицу с(6×6). Значения элементов главной диагонали должны совпадать с номером строки/столбца.
Решение. Для получения диагональной матрицы в системе предусмотрена функция diag, которая имеет один параметр – вектор диагональных элементов. Поэтому формирование матрицы начнем с создания вспомогательного вектора, в который занесем элементы для диагонали. Для формирования этого вспомогательного вектора (например, с именем s), воспользуемся вспомогательной переменной, которая будет играть роль индекса (например, i). Тогда формирование диагональной матрицы может быть получено в результате операций, как это показано на рис. 3.6.
Рис. 3.6. Формирование диагональной матрицы
Пример 4. Даны две матрицы: А(4×3) и В(4×2). Требуется объединить эти матрицы в одну матрицу С(4×5), причем, первыми столбцами новой матрицы должны быть столбцы матрицы А, а справа от этих элементов следовать столбцы матрицы В (методом «дописывания справа»).
Решение. Для соединения двух матриц в одну матрицу можно использовать функцию augment, параметрами которой будут являться имена соединяемых матриц, как это показано на рис. 7.7.
Рис. 3.7. Объединения двух матриц по правилу «дописывания справа»
Пример 5. Даны две матрицы: А(2×3) и В(3×3). Требуется объединить эти матрицы в одну матрицу С(5×3), причем, в новой матрицы в качестве первых строк должны быть строки матрицы А, а за ними должны следовать строки матрицы В.
Решение. Для соединения двух матриц в одну матрицу по правилу «друг под другом» можно использовать функцию stack, параметрами которой будут являться имена соединяемых матриц, как это показано на рис. 3.8.
Рис. 3.8. Объединения двух матриц по правилу «друг под другом»
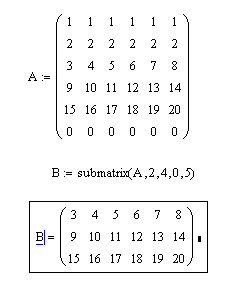
Пример 6. Дана матрица А(6×6). Требуется получить из этой матрицу подматрицу, в которую включить элементы, расположенные в строках, начиная с номера 2-го по номер 4-ый, и столбцах, начиная с номера 0-го по номер 5-ый.
Решение. Для выделения подматрицы с номерами столбцов и строк представленными граничными значениями предусмотрена функция submatrix. Эта функция имеет 5 параметров: имя матрицы, из которой производится выбор; начальный номер строки выбора; конечный номер строки выбора; начальный номер столбца выбора; конечный номер столбца выбора. Возможное решение представлено на рис. 3.9.
Рис. 3.9. Выделение подматрицы из заданной матрицы
Пример 7. Дана матрица А(6×6). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с 4–ым столбцом матрицы А, а второй – с 3-ей строкой матрицы А.
Решение. Для получения векторных значений можно воспользоваться командой М (из матрицы взять вектор-столбец), которая расположена на панели «Мatrix». Для получения первого вектора эту команду нужно применить непосредственно к матрице А, а для получения второго вектора нужно сначала получить из матрицы Атранспонированную матрицу, а только потом воспользоваться командой «взять столбец». Возможное решение представлено на рис. 3.10.
Рис. 3.10. Выделение векторных значений из заданной матрицы
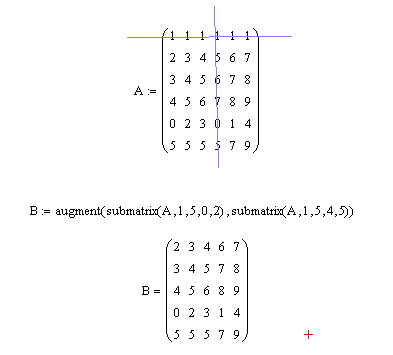
Пример 8. Из матрицы А(6×6) выделить минор, который образуется в результате вычеркивания из этой матрицы нулевой строчки и третьего столбца.
Решение. Решение задачи можно свести к соединению двух подматриц, выделенных из матрицы А, как это показано на рис. 3.11.
Рис. 3.11. Выделение минора из заданной матрицы
Видео:Основные действия с матрицами и векторами в MathCAD 14 (20/34)Скачать

3.2. Использование матриц специального вида для выполнения матричных операций в системе MathCad
Известно, что в результате умножении матрицы на вектор получается вектор. Причем, каждый i–ый элемент этого вектора-результата представляет собой сумму попарных произведений соответствующих элементов i–ой строки матрицы на элементы вектора-сомножителя. Очевидно, если в векторе, на который умножается матрица, все элементы равны нулю, а один элемент равен единице, то результатом такого произведения будет число, соответствующее тому элементуi–ой строки матрицы, где векторным сомножителем будет единица. Такой вывод можно использовать для выделения (формирования) из матрицы нужного столбца.
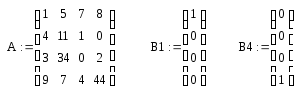
Пример 9. Даны матрица: А(4×4). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с 0–ым столбцом матрицы А, а второй — с 3-им столбцом матрицы А.
Решение. Для получения новых векторов сформируем два вспомогательных вектора: вектор B1 – с единичным значением в строке с номером 0, а второй вектор В4 – с единичным значением в строке с номером 3. Тогда для получения векторов в соответствии с условием задачи достаточно умножить матрицу А справа на векторы В1 и В2, как это показано на рис. 3.12.
Рис. 3.12. Выделение векторных значений из заданной матрицы
Аналогичным образом можно получить вектор-строку из матрицы. Для этого достаточно сформировать вспомогательный вектор — строку, у которой все компоненты равны нулю, а одна компонента, номер которой соответствует номеру выделяемой строки из матрицы, равна единице. Если этот вектор умножить слева на матрицу, то в результате будет получена нужная строка.
Пример 10. Дана матрица: А(4×4). Требуется выделить из матрицы первую строку по порядку (с номером 0).
Решение. Сначала требуется подготовить вспомогательный вектор-строку, а потом умножить эту строку слева на матрицу А. Вектор-строку можно получить из предыдущего примера транспонированием вектора-столбца В1.
Такой прием можно использовать для перестановки строк и столбцов матрицы, только для этого потребуется уже вспомогательная матрица, состоящая из векторов-столбцов (векторов-строк), место единичных элементы которых соответствуют тому порядку, который нужно иметь в результате преобразования матрицы.
Пример 11. Дана матрица: А(4×4). Требуется переставить в матрице строки с номерами 0 и 1.
Решение. Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в строках должно соответствовать нужному порядку для расположения строк в новой матрице. После этого решение можно получить простым перемножением матриц:
Пример 12. Дана матрица: А(4×4). Требуется переставить в матрице столбцы с номерами 0 и 1.
Решение. Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в столбцах соответствуют нужному порядку для выбора их в новую матрицу. После этого решение можно получить простым перемножением матриц:
Рассуждая, таким образом, можно с помощью вспомогательного вектора с единичными компонентами получить вектор, компоненты которого будут равны сумме строк (столбцов) матрицы, а также суммы отдельно выделенного столбика (строчки).
Пример 13. Дана матрица: А(4×4). Требуется найти сумму элементов в столбце с номером 3.
Решение. Для решения задачи требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение:
Пример 14. Дана матрица: А(4×4). Требуется получить вектора, элементы которого будут представлять суммы элементов в столбцах матрицы.
Решение. Для решения требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение:
Видео:МАТКАД МатрицыСкачать
3.3. Решение систем линейных алгебраических уравнений с использованием матричных преобразований
Для простоты решения ограничимся случаем системы из трех линейных уравнений с тремя неизвестными. Рассуждения на случай большего числа уравнений можно провести аналогичным образом. Пусть требуется найти решение система линейных алгебраических уравнений (СЛАУ) вида:

Введем следующие обозначения:
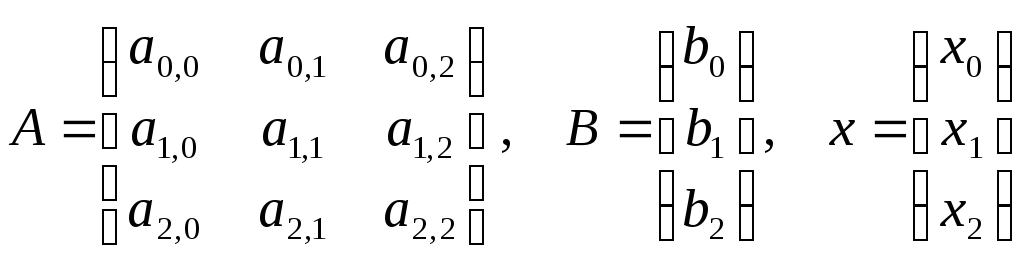
А – матрица коэффициентов;
В – вектор свободных членов;
х – вектор неизвестных.
В обозначениях (5.2) систему уравнений (5.1) можно записать в виде:
Из линейной алгебры известно, что система (3.3) имеет единственное решение при условии невырожденности матрицы, т.е. её детерминант должен быть отличным от нуля. Поэтому, какой бы вычислительный метод не применялся, решение системы линейных уравнений всегда нужно начинать с вычисления определителя (детерминанта) матрицы.
В разделе 6.4 мы уже рассматривали решение систем с использованием блока решения. Если применить к уравнению (3.3) аппарат матричных преобразований можно получить «матричную» формулу для вычисления x:
Помножим уравнение (3.3) слева на матрицу, обратную к матрице А:
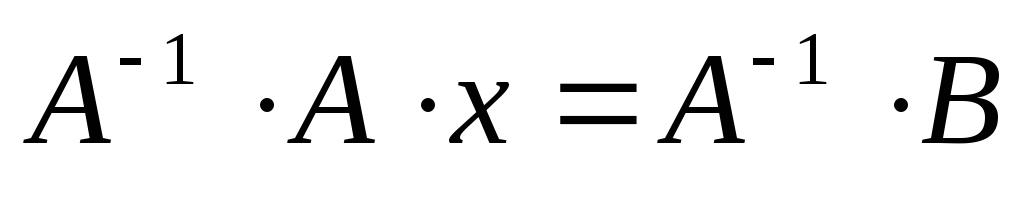
Воспользуемся свойством, что 
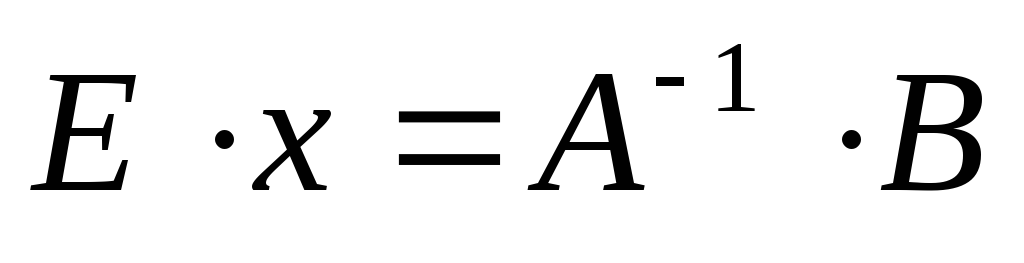
Воспользуемся свойством, что Ex = x. Тогда уравнение (3.5) примет вид:

где (3.6) – решение системы (3.3).
Пример 15. Требуется найти решение следующей системы линейных уравнений:
Решение. Решение СЛАУ матричным способом в системе MathCAD приведено на рис.3.13.
Видео:Создание матриц в MathCAD 14 (18/34)Скачать
MathCAD — это просто! Часть 10. Работа с векторами и матрицами
Снова здравствуйте. Мы с вами успели вполне успешно закончить со школьной алгеброй, и, значит, можем переходить к более сложным вещам — например, к тому разделу математики, который в университетах обычно называют линейной алгеброй. Конечно, раздел этот весьма и весьма обширен, и нечего даже думать о том, чтобы охватить хотя бы большую его часть. Тем не менее, нам с вами, я так думаю, кое-что из него научиться использовать практически вполне по силам — к примеру, мы можем научиться работать в MathCAD’е с векторами и матрицами. Эти два понятия — важнейшие математические абстракции, роль которых трудно переоценить в научно-техническом прогрессе. Ведь именно применение векторов и векторного анализа позволило в свое время Оливеру Хевисайду сократить количество уравнений Максвелла, описывающих электромагнитное поле, с двух десятков до всего лишь четырех. До векторного анализа, я так думаю, мы с вами в свое время еще доберемся, ну, а пока займемся более прозаическими вещами. Какими именно? Думаю, все станет ясно, если вы продолжите читать эту статью.
Немного об элементах матриц
Хотя дальше мы будем иметь дело и с векторами, и с матрицами, я краткости ради буду говорить просто «матрица», подразумевая, что под вектором мы будем иметь в виду частный случай матрицы, а именно ту ее разновидность, которая представляет собой одиночный столбец. Если же вектор будет представлять собой строку, то это будет специально оговорено. Впрочем, думаю, до этого дело вряд ли дойдет. С матрицами, вообще говоря, мы с вами работать уже немного умеем. Ну, не то чтобы прямо так вот работать — по крайней мере, вводить их в MathCAD’е мы уже вводили. Тем не менее, думаю, будет не лишним напомнить, что ввести в рабочую область матрицу можно с помощью кнопки Matrix or Vector, расположенной на панели Matrix, либо с помощью сочетания горячих клавиш Ctrl+M. Впрочем, мы с вами пока не затрагивали один небольшой, но крайне важный момент, а именно как обращаться в вычислениях не к матрице целиком, а к отдельным ее элементам. Сделать это, на самом деле, очень просто. Пусть у нас задана квадратная матрица X размером два на два элемента. Верхний левый элемент будет иметь индексы 0,0; нижний правый, соответственно, будет иметь индексы 1,1. То есть, как видите, элементы матрицы нумеруются с нуля. Это, в общем-то, довольно удобно, однако, если для вас привычнее нумеровать их с единицы, или, скажем, с 1024-х, то можно поменять значение встроенной переменной ORIGIN, введя в самом начале документа MatchCAD в строку (без кавычек). Или, соответственно, «ORIGIN := 1024». Можно поменять значение переменной и в окне опций MathCAD’а, выбрав в меню Tools пункт Worksheet options и на вкладке Built-In Variables поменяв значение переменной ORIGIN на нужное вам.
Так вот, вернемся к нашим элементам матрицы. Чтобы «вынуть» из нее первый элемент, нужно написать следующее: X0, 0. Для того, чтобы записать индексы внизу от имени переменной, которая обозначает матрицу, можно воспользоваться кнопкой Subscript со все той же панели инструментов для матричных и векторных вычислений или с клавиатуры перейти в нижний индекс клавишей «[» (русское «х»). Обратите внимание, что для разделения индексов, обозначающих строку и столбец, используется запятая. Элементы матрицы можно не только извлекать из матрицы, заданной таблично. Вы можете задать несколько элементов с соответствующими индексами по ходу вычисления, а после уже MathCAD самостоятельно сформирует из них матрицу (но только когда вы зададите уже все ее элементы — в противном случае незаданным элементам будут присвоены нулевые значения). Вы можете использовать ранжированные переменные для задания элементов матрицы. Временами это бывает не просто удобно, а очень удобно. Так, к примеру, можно задать для матрицы X следующую формулу, описывающую значения каждого ее элемента i-й строки и j-го столбца: Xi, j := i * j. Перед таким определением элементов матрицы остается только определить диапазон, в котором будут изменяться i и j. Я для примера взял значения i := 0..5 и j := 0..5, но вы, конечно же, можете установить любой другой нужный вам диапазон в зависимости от требований вашей задачи, решаемой с помощью матриц в среде MathCAD.
Операции над матрицами
Конечно, у применения матриц в реальных задачах существует множество интересных и не очень аспектов, однако все они рано или поздно упираются в необходимость проведения с матрицами простых алгебраических операций. Проводить их вручную — задача трудоемкая, и можно потратить время с гораздо большей пользой, переложив рутинную работу на MathCAD. Для начала познакомимся с теми функциями, которые собственно никаких математических операций не выполняют, но при этом являются весьма важными в действиях с матрицами. Эти функции позволяют объединять две матрицы в одну (не складывать матрицы, а просто объединять их элементы) и выделять из матрицы другую матрицу. Первая из функций — augment. Она объединяет две матрицы, имеющие одинаковое число строк, таким образом, что из них образуется одна, в которой элементы этих двух располагаются, что называется, «плечом к плечу». В качестве аргументов этой функции нужны только две объединяемые матрицы. Ее аналог для тех матриц, которые имеют одинаковое число столбцов, и должны быть объединены одна над другой, является функция stack. Ее аргументами тоже должны быть две объединяемые матрицы. Функция же, которая не объединяет, а, напротив, «разрезает» матрицы, имеет название submatrix. Для нее нужно указывать имя матрицы, из которой мы хотим выделить подматрицу, и координаты элементов новой матрицы в старой матрице. То есть для того, чтобы вырезать матрицу 4х4 из верхних левых элементов матрицы размером 5х5, нам нужно вызывать эту функцию со следующими параметрами: submatrix(Y, 0, 4, 0, 4). Здесь Y — это, конечно же, имя матрицы размером 5х5 элементов. Демонстрацию использования всех этих функций применительно к конкретным матрицам можно увидеть на соответствующей иллюстрации к статье.
Теперь, я так думаю, самое время перейти уже к арифметическим операциям над матрицами. Вы увидите, что их использование в MathCAD не потребует от вас никаких специальных знаний в области линейной алгебры — не считая, конечно, общих представлений о том, как работают матричные операции, для понимания того, что может получиться в их итоге. MathCAD хорош для пользователя тем, что позволяет ему работать с векторами и матрицами точно так же, как с обычными скалярами, сиречь переменными, содержащими исключительно и только действительные числа. Попробуйте задать две матрицы (я их назвал aa и bb), а затем применить к ним операцию сложения точно так же, как когда-то применяли ее к обыкновенным числам. Конечно, для того, чтобы матрицы можно было складывать, они должны иметь одинаковые размеры. Точно так же можете попробовать вычесть из одной матрицы другую или перемножить их. Вы увидите, что MathCAD успешно справляется с подобными задачами, не напрягая пользователя излишними вычислениями.
Транспонировать матрицы в MathCAD’е ничуть не сложнее, чем их складывать или перемножать. Вычислять обратные матрицы, впрочем, тоже. Во всех этих задачах помогут соответствующие операторы с Они обозначены на ней теми же значками, что и в учебниках по линейной алгебре, а потому пользователю, хотя бы минимально знакомому с матричным исчислением, все должно быть просто и понятно. Нужно только помнить, что нельзя вычислить обратную матрицу для той матрицы, которая является вырожденной (то есть имеет нулевые или пропорциональные друг другу строки или столбцы). Для того, чтобы не останавливаться излишне подробно на этих простых операциях, просто приведу иллюстрацию, демонстрирующую их практическое использование. Думаю, у читателей не возникнет никаких проблем ни с транспонированием, ни с вычислением обратной матрицы с помощью MathCAD.
Еще одной часто выполняемой операцией является вычисление детерминанта, или определителя матрицы. Думаю, что совсем не огорчу вас известием о том, что в MathCAD и с определителями работать так же просто, как и со всем остальным, связанным с матрицами. За его вычисление отвечает кнопка Determinant, расположенная, конечно же, на панели Matrix. Поскольку детерминант в MathCAD’е, как и вообще в линейной алгебре, обозначается с помощью символов прямых черт, ограничивающих матрицу (или имя переменной, ее обозначающей), то вполне логично, что вставить эти самые прямые черты в текст выражения можно с помощью соответствующей клавиши на клавиатуре: Shift + . Думаю, этой несложной комбинацией будет пользоваться все же удобнее, чем искать каждый раз нужную кнопку на панели инструментов MathCAD’а.
Внешний вид матриц
Мы с вами, конечно же, далеко еще не закончили свое знакомство с матрицами в MathCAD’е, однако, думаю, на сегодня уже непосредственной математики хватит. В конце статьи я лучше расскажу о том, как можно изменить способ отображения матриц в среде MathCAD — возможно, кому-то из читателей этой статьи эта информация будет полезной и небезынтересной.
Дело в том, что MathCAD может отображать матрицы не только в привычном всем виде чисел, заключенных в скобки, но и в виде таблиц. Если вы используете этот математический пакет для каких-либо статистических расчетов и при этом работаете с большими массивами данных, то, безусловно, такое отображение матриц будет более предпочтительным для вас, чем традиционное. Для изменения способа отображения матриц дважды кликните по нужной матрице и в появившемся окне перейдите на вкладку Display Options. Далее в поле Matrix display style выберите значение Table. Матрица приобретет вид точно такой, как на соответствующей иллюстрации к этой статье.
Внешний вид таблицы можно также настроить далее, кликнув по ней правой кнопкой мыши и выбрав пункт Properties. В появившемся окне можно снять птичку с пункта Show column/row labels, чтобы убрать отображение нумерации строк и столбцов в матрице, представляемой в виде таблицы. На вкладке Data Range можно выбрать диапазон отображаемых строк и столбцов матрицы, что также полезно для матриц, содержащих большое количество элементов.
Ну что ж, на сегодня, думаю, достаточно. Это только начало работы с матрицами — в следующий раз мы поговорим о гораздо более интересных вещах, чем просто сложение, транспонирование и вычисление детерминанта.
Компьютерная газета. Статья была опубликована в номере 23 за 2008 год в рубрике soft
🌟 Видео
Матрицы. Скалярное и векторное произведение векторов в Mathcad, матричные функции(Урок 3.3)Скачать
Функции для работы с матрицами и векторами в MathCAD 14 (21/34)Скачать
MathCAD Простейшие действия с матрицамиСкачать
Векторы и матрицыСкачать
Занятие 12. Векторы и матрицыСкачать

Программа MathCAD. Урок 10. Работа с матрицами в MathCADСкачать

Оператор векторизации в MathCAD 14 (23/34)Скачать

Матрицы и векторы. Настройки Mathcad при работе с матрицами. Урок 12Скачать

Код сверхспособностей по дате рождения. НумерологияСкачать

MathCAD Создание матрицСкачать

Матрицы и векторыСкачать

Матрицы и векторы. Создание матриц и основные операции с ними. Урок 11Скачать

Работа с массивами. Вектор столбцы и вектор строки 1. Урок 7Скачать

MATLAB 04 Массивы и матрицыСкачать

Урок 10 Собственные векторы и собственные значения матрицыСкачать