Двоичным (булевым) n-мерным вектором называют набор из n чисел (b1, b2, . bn), каждое из которых может принимать только значения в двоичной системе счисления – 0 или 1.
Двоичный вектор 
является обратным (инвертированным) к 
, если он образован из заменой всех нулей единицами, а единиц – нулями.
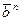
Например, если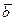 
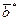
= (0,1,1,1,0,1), то 
= (1,0,0,0,1,0).
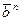
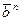
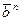
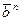
Если в записи двоичного вектора длины n устранить запятые, его можно рассматривать как двоичную запись некоторого целого числа. Наименьшим таким числом является 0. Ему соответствует вектор = (0, . 0). Наибольшим является число 2 n – 1, которому соответствует вектор = (1, . 1). Следовательно, при помощи полного набора двоичных векторов длины n можно записать все 2 n целых чисел из отрезка
[0,2 n –1]. Такие числа называют порядковыми номерамивекторов. Их используют как в двоичном виде, так и в десятичной системе счисления.
Пример 1.Найти порядковый номер булева вектора 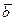= (1,0,0,1,0,1) в десятичной системе счисления.
Решение. Устраняя запятые в векторе, получим двоичную запись 1001012. Переводя ее по правилу 2.1.1 в десятичную систему счисления, получим:
1001012 =1×2 5 +1×2 2 +1×2 0 =3210 +410 +110 =3510.
Ответ: десятичный порядковый номер заданного булева вектора равен 3510.
В качестве меры близости булевых векторов используют расстояние Хэмминга.
Определение.Расстоянием Хемминга r между булевыми векторами `a n и`b n называют величину r(`a n , `b n ), которая равна числу координат, по которым различаются векторы `a n и`b n .
Пример 8. r(100011, 110011)=1, r(0101, 1010)=4.
Определение. Булевы векторы`a n и`b n , различающиеся ровно по одной координате ( r (`a n ,`b n ) = 1), называют соседними.
Рассмотрим наиболее употребительные геометрические интерпретации булевых n – мерных векторов.
1. Представление в виде двоичных чисел. Если в записи вектора `b n устранить запятые, ее можно рассматривать как двоичную запись некоторого целого числа. Наименьшим таким числом является 0. Ему соответствует вектор `b n =(0, . 0). Наибольшим является число 2 n – 1, которому соответствует`b n = (1, . 1). Следовательно, при помощи векторов `b n можно записать все 2 n целых чисел из интервала [0, 2 n – 1]. Такие числа будем называть порядковыми номерами векторов.
Лексикографическим называют такой порядок векторов`b n , когда соответствующие им двоичные числа расположены по возрастанию от 0 до 2 n – 1.
В качестве примера рассмотрим полное множество 3-мерных двоичных векторов, расположенных в лексикографическом порядке:
0 (0, 0, 0), 4 (1, 0, 0),
1 (0, 0, 1), 5 (1, 0, 1),
2 (0, 1, 0), 6 (1, 1, 0),
3 (0, 1, 1), 7 (1, 1, 1).
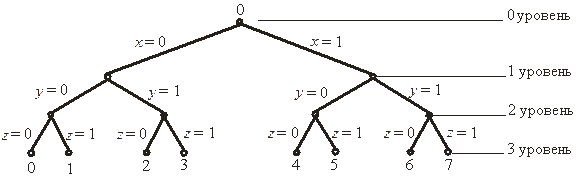
2. Бинарное дерево Т n . Сопоставим множеству всех 2 n векторов`b n следующую древовидную структуру, начинающуюся
в корневой вершине О (вершине нулевого уровня). Из нее выходят вниз два отрезка (ребра), соответствующие значениям b1=0(влево) и b1=1(вправо) и оканчивающиеся вершинами первого уровня. Из них выходят вниз по два ребра, соответствующие b2=0(влево) и b2=1(вправо) и оканчивающиеся новыми вершинами — второго уровня и т. д. Процесс завершается построением всех вершин n-го уровня. Данная структура называется
бинарным деревом и обозначается Т n . На рис. 4.1 показано
дерево Т 3 для 3-мерного булевого вектора`b 3 =(х, у, z).
Рис. 4.1. Бинарное дерево Т 3
Пронумеруем слева направо все вершины n-го уровня от 0до
2 n – 1. Каждому вектору `b n можно однозначно поставить
в соответствие путь из корневой вершины О в вершину n–го уровня с порядковым номером вектора `b n . Например, вектору (0,1,0)в рассмотренном примере соответствует путь из корневой вершины в вершину 2 (0102 = 210) по ребрам х = 0, у = 1, z = 0. Таким образом, бинарное дерево полностью описывает все 2 n векторов`b n .
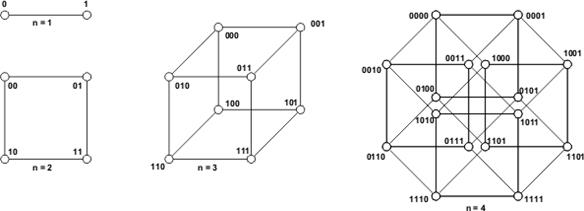
3. Единичный n-мерный куб В n . Единичным n-мерным кубом называют полный набор вершин, соответствующих векторам`b n , в котором каждые две соседних вершины (которым соответствуют векторы, различающиеся ровно по одной координате) соединены отрезком (ребром). Обозначается единичный n-мерный куб как В n . На рис. 4.2 показаны кубы В 1 , В 2 , а также плоские проекции кубов В 3 , В 4 .
Определение. Дана вершина`a n в В n . Множество вершин В n <bn >, для которых r(a n ,`b n )= r, называют сферой радиуса r. Множество <gn > вершин В n , для которых r(a n ,`g n )£ r, называют шаром радиуса r.
Рис. 4.2. Единичные n-мерные кубы В 1 , В 2 и плоские проекции кубов В 3 , В 4
Вопросы для проверки знаний.
1. Есть ли принципиальное различие правил выполнения сложения и вычитания в десятичной системе счисления и других системах с постоянными основаниями?
2. Какой формат компьютерного представления чисел называют беззнаковым целым числом?
3. Какой формат компьютерного представления чисел называют целым числом со знаком?
4. Какой способ компьютерного представления целых чисел называют прямым кодом?
5. Какой способ компьютерного представления целых чисел называют дополнительным кодом?
6. Для каких целых чисел прямой код совпадает с дополнительным кодом?
7. Может ли целое число занимать в электронной памяти а) 4 бита, б) 6 бит, в) 8 бит, г) 10 бит?
8. По каким правилам осуществляется перевод беззнаковых байтовых целых чисел из прямого кода в дополнительный и обратно?
9. По каким правилам осуществляется перевод байтовых целых чисел со знаком из прямого кода в дополнительный и обратно?
10. В каких случаях вычитание байтовых беззнаковых целых чисел дает результат в прямом коде, а в каких – в дополнительном?
11. Что называют двоичным (булевым) n-мерным вектором?
12. Какую операцию называют инвертированием булевого вектора?
13. Какие числа называют порядковыми номерами булевых векторов?
14. Что называют лексикографическим порядком двоичных векторов?
- Лекция 02. Теория булевых функций. Булева алгебра
- Вектор в дискретной математике
- Знакомимся с вектором
- Линейная алгебра
- Что такое вектор
- Как записывать
- Скаляр
- Как изображать
- И зачем нам это всё
- Что дальше
- Лекция 02. Теория булевых функций. Булева алгебра
- Элементы дискретной математики: конспект лекций (стр. 1 )
- ВВЕДЕНИЕ
- Глава 1. МНОЖЕСТВА И ОТНОШЕНИЯ
- 1.1. Множества
- 1.2. Задание множеств
- 1.3. Операции над множествами
- 💥 Видео
Видео:Характеристические векторы множествСкачать
Лекция 02. Теория булевых функций. Булева алгебра
Множество M с двумя введенными бинарными операциями (& V), одной унарной операцией (*) и двумя выделенными элементами называется булевой алгеброй, если выполнены следующие свойства (Аксиомы булевой алгебры). Названия операций пока не введены.
1. X & Y = Y&X, X V Y = Y V X – коммутативность.
2. (X & Y) & Z = X & (Y & Z), (X V Y) V Z = X V (Y V Z) – ассоциативность.
3. (X V Y) & Z = (X & Z) V (Y & Z), (X & Y) V (Y & Z) = (X V Z) & (Y & Z) – дистрибутивность.
4. Поглощение – X & X = X, X V X = X.
5. Свойства констант
X & I = X, где I – аналог универсального множества.
6. Инвальтивность (X*)* = X
7. Дополнимость X V X* = I, X & X* = 0.
8. Законы двойственности – (X & Y)* = X* V Y*, (X V Y)* = X* & Y
Булева алгебра всех подмножеств данного множества.
Легко показать, что свойства операций над множествами совпадают со свойствами (аксиомами) булевой алгебры. То есть, Множество P(U) с операциями объединения, пересечения и дополнения является булевой алгеброй.
Oбъединение эквивалентно V, пересечение — &, дополнение — *, пустое множество – 0, а универсальное – I.
Все аксиомы булевой алгебры справедливы в операциях над множествами.
Видео:Математика это не ИсламСкачать
Вектор в дискретной математике
Видео:Множества и операции над нимиСкачать
Знакомимся с вектором
Основы линейной алгебры для тех, кого это миновало в универе.
Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.
Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.
⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать
Линейная алгебра
Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.
Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.
Например, мы знаем, что если a + b = c , то a = c − b . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.
Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.
В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.
Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.
Видео:Булевы функции. Функции алгебры логики. Что это?Скачать
Что такое вектор
Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.
Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве
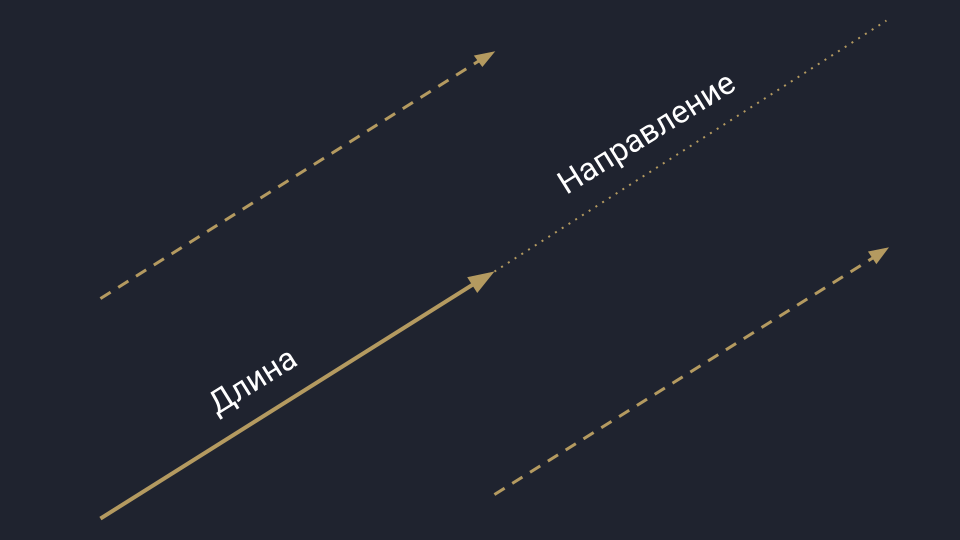
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.
Аналитическое представление вектора: данные можно перевести в числа
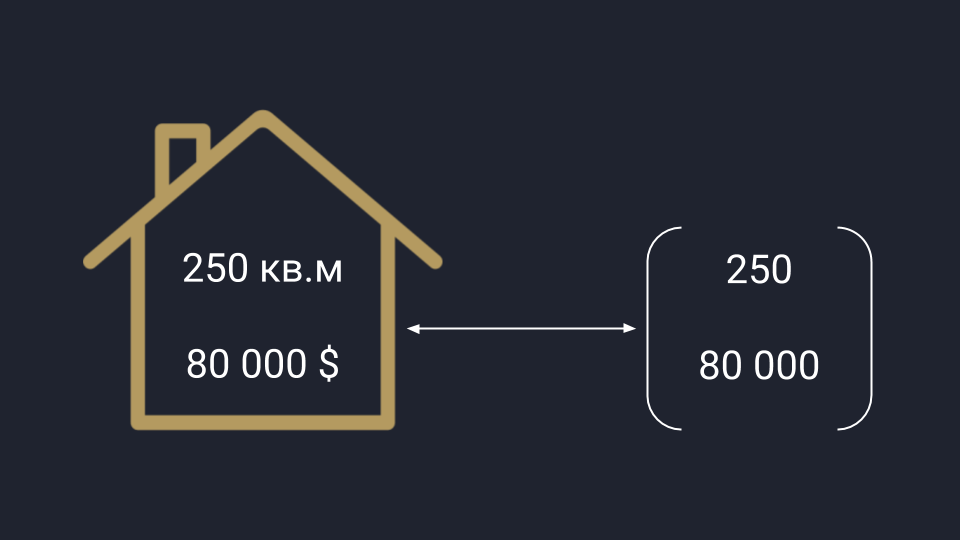
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.
Математическое представление вектора: данные можно перевести в числа или график
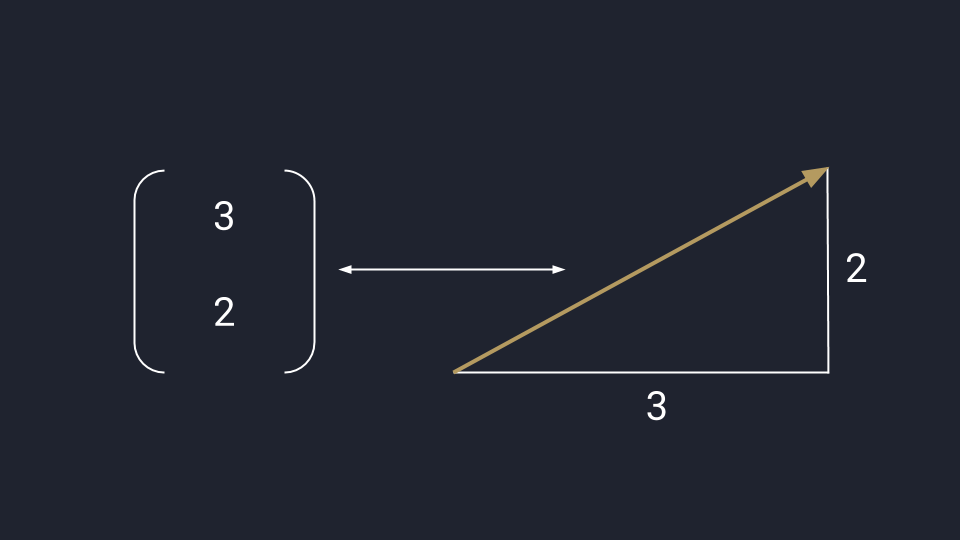
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.
Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат
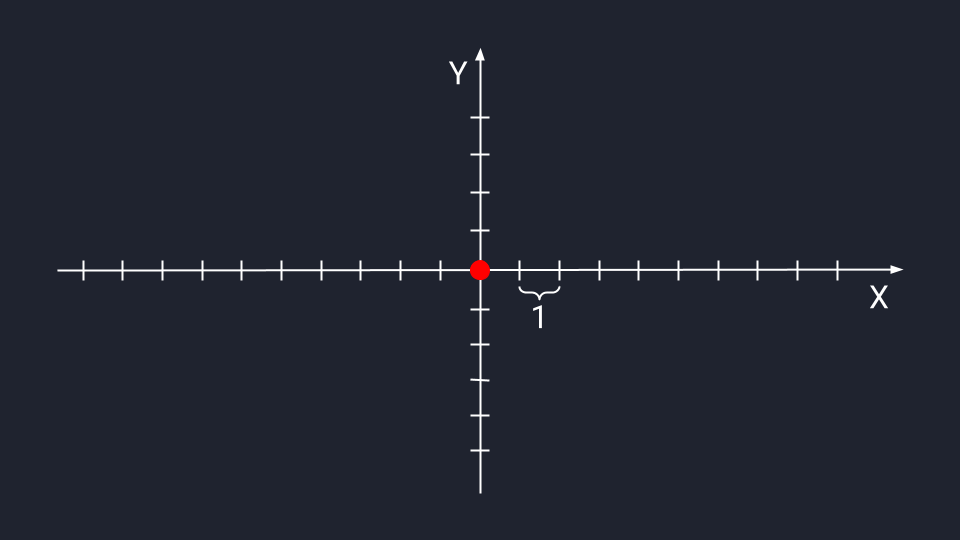
👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.
Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать
Как записывать
Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.
Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.
Способы записи вектора
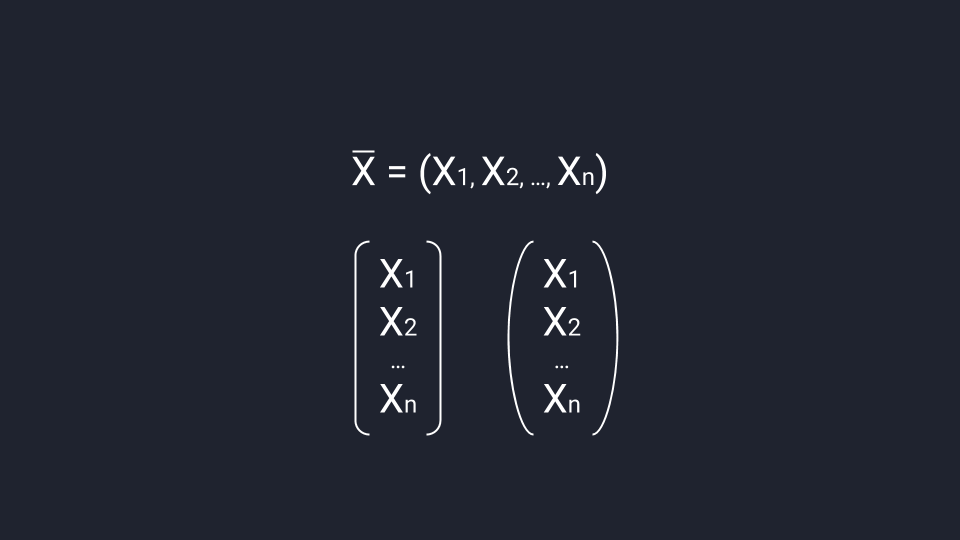
Скаляр
Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.
Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать
Как изображать
Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.
Графическое представление скаляра. Записывается в круглых скобках
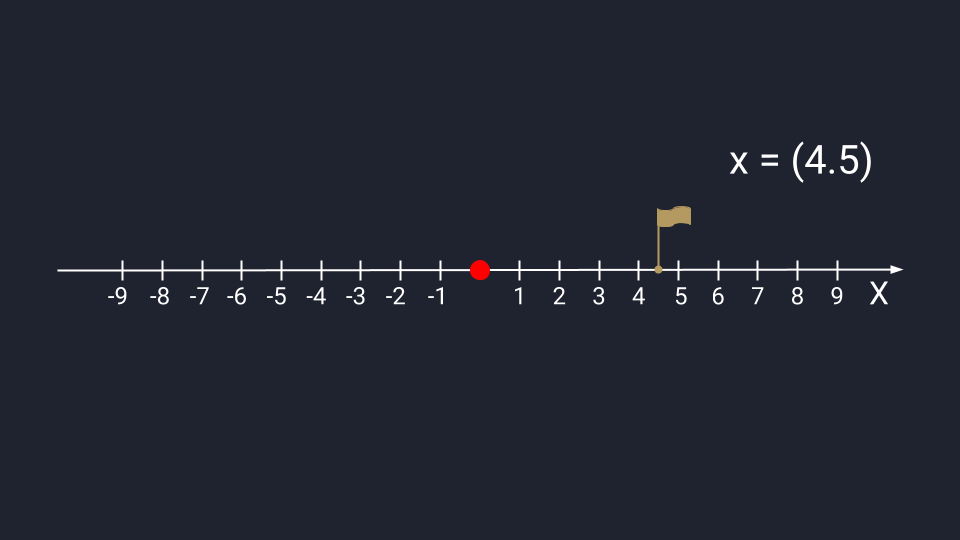
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.
Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.
Графическое представление числового вектора в двух измерениях
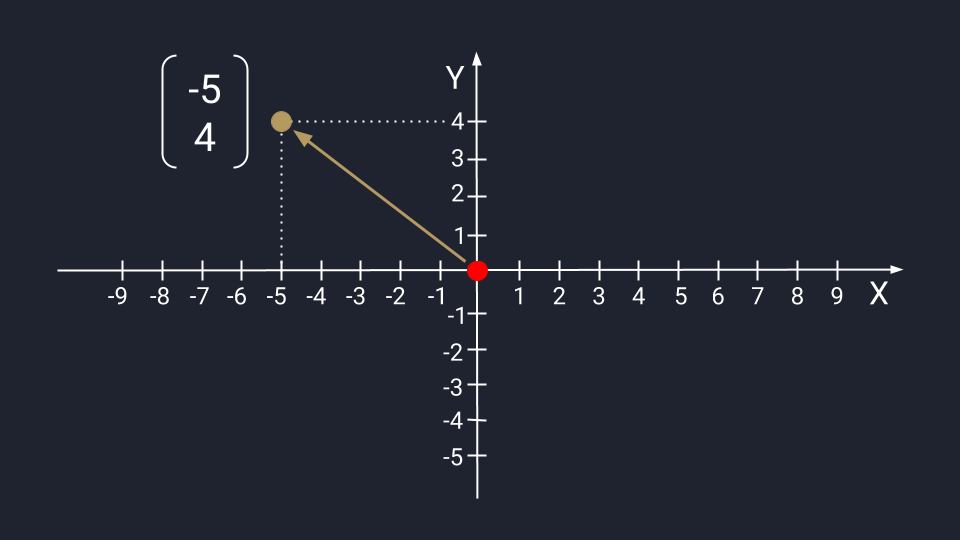
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.
Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.
Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4
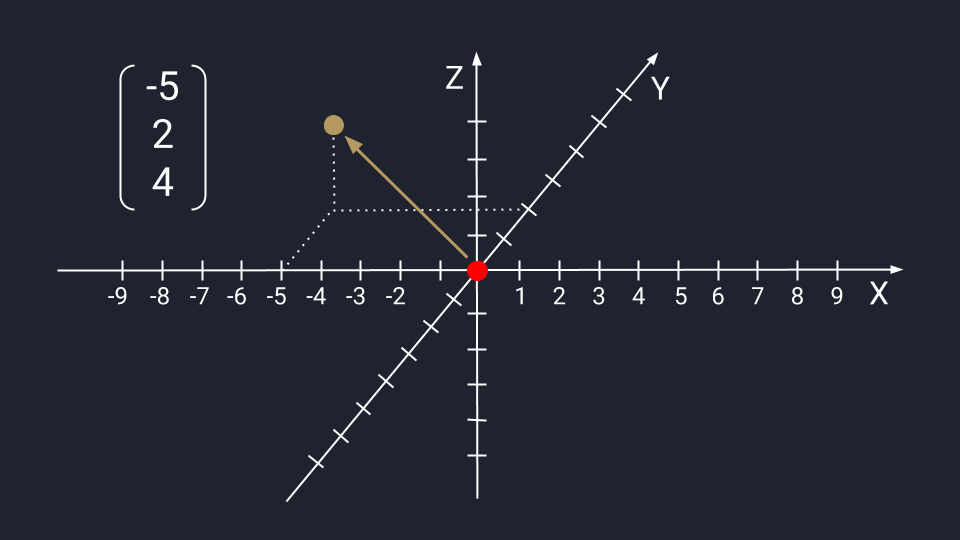
Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.
Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.
Видео:День студента мехмата МГУ #мгу #умскул #физика #математика #учеба #подготовкаогэ #подготовкакегэСкачать
И зачем нам это всё
Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:
- На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
- Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.
Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.
И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.
Видео:Дельта альфа альфа штрих | МФТИСкачать
Что дальше
В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.
Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать
Лекция 02. Теория булевых функций. Булева алгебра
Множество M с двумя введенными бинарными операциями (& V), одной унарной операцией (*) и двумя выделенными элементами называется булевой алгеброй, если выполнены следующие свойства (Аксиомы булевой алгебры). Названия операций пока не введены.
1. X & Y = Y&X, X V Y = Y V X – коммутативность.
2. (X & Y) & Z = X & (Y & Z), (X V Y) V Z = X V (Y V Z) – ассоциативность.
3. (X V Y) & Z = (X & Z) V (Y & Z), (X & Y) V (Y & Z) = (X V Z) & (Y & Z) – дистрибутивность.
4. Поглощение – X & X = X, X V X = X.
5. Свойства констант
X & I = X, где I – аналог универсального множества.
6. Инвальтивность (X*)* = X
7. Дополнимость X V X* = I, X & X* = 0.
8. Законы двойственности – (X & Y)* = X* V Y*, (X V Y)* = X* & Y
Булева алгебра всех подмножеств данного множества.
Легко показать, что свойства операций над множествами совпадают со свойствами (аксиомами) булевой алгебры. То есть, Множество P(U) с операциями объединения, пересечения и дополнения является булевой алгеброй.
Oбъединение эквивалентно V, пересечение — &, дополнение — *, пустое множество – 0, а универсальное – I.
Все аксиомы булевой алгебры справедливы в операциях над множествами.
Видео:Введение в дискретную математикуСкачать
Элементы дискретной математики: конспект лекций (стр. 1 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 |
учебно-методической комиссией филиала ЮУрГУ в г. Златоусте
к. ф.-м. н. доц. , д. т. н. проф.
Элементы дискретной математики: конспект лекций / . – Челябинск: Изд. ЮУрГУ, 2008. – 102 с.
В конспекте лекций излагается теория множеств, комбинаторики, отношений, переключательных функций, теории графов в объеме, предусмотренном Госстандартом специальностей, связанных с программированием, вычислительной техникой. В конце каждой главы приведены упражнения для закрепления теоретического материала.
Предназначен для студентов технических университетов, обучающихся по направлению «Информатика и вычислительная техника».
ã Издательство ЮУрГУ, 2008
Видео:Дискретная математика. Булевы функции и формулыСкачать
ВВЕДЕНИЕ
Дискретная математика или дискретный анализ – сравнительно новое направление в математике, объединяющее отдельные её разделы, ранее сформированные как самостоятельные теории. К ним относятся математическая логика и теории множеств, графов, кодирования, автоматов.
Дискретной математикой называют совокупность математических дисциплин, изучающих свойства абстрактных дискретных объектов, т. е. свойства математических моделей объектов, процессов, зависимостей, существующих в реальном мире, которыми оперируют в различных областях знаний. Таким образом, дискретный анализ – самостоятельный раздел современной математики, изучающий свойства различных структур, имеющих конечный характер. Они могут возникать как в самой математике, так и в её приложениях. К их числу принято относить объекты, имеющие прерывный (дискретный) характер в отличие от объектов, изучаемых классической математикой и носящих непрерывный характер.
Вообще говоря, деление математики на дискретную и классическую достаточно условно. Например, аппарат теории множеств и теории графов используется при изучении не только дискретных, но и непрерывных объектов. С другой стороны, сама дискретная математика использует средства, разработанные в классической математике. Однако характер объектов, исследуемых дискретной математикой, настолько своеобразен, что методов классической математики не всегда достаточно для их изучения. Поэтому те специфические методы, которые применяются для очень широкого класса конечных дискретных объектов, и были объединены в общее направление – дискретную математику.
XXI в. называют веком информатизации, когда основной объём информации хранится в памяти ЭВМ. Любому человеку, стремящемуся ею воспользоваться, необходимо освоить азы «безбумажной информатики». Применение ЭВМ для комплексной автоматизации информационной деятельности принципиально изменило характер взаимоотношений человека и машины. Если раньше компьютер осваивали только те, кто непосредственно его обслуживал: программисты, электронщики, операторы, то в XXI в. без машинной обработки информации не обойдется ни одна отрасль деятельности.
В последнее время раздел математики, называемый «Дискретный анализ», всё чаще вводится в программы подготовки не только математиков, инженеров, программистов, но даже юристов. Интерес к этой дисциплине не случаен, так как потребность в знаниях этой области математики объясняется широким кругом её применения: электроника и информатика, вопросы оптимизации и принятия решений.
Методы, разрабатываемые дискретной математикой, используются в различных областях знаний. Так, теоретическая информатика (или теоретическая кибернетика) использует математические методы для построения и изучения моделей обработки, передачи и использования информации. Объекты её изучения – дискретные множества. Теоретическая информатика является как поставщиком задач, так и потребителем методов дискретной математики.
Теория автоматов разрабатывает методы, с помощью которых можно на основе моделей логического типа изучать процессы, протекающие в самой машине во время её работы. Для работы на компьютере информацию представляют в дискретной форме, позволяющей переводить её в программы, понятные ЭВМ.
Теория информации изучает вид тех форм, в которых информация представляется в компьютере. Формализация любой информации, реально существующей в живой и неживой природе, происходит через компьютерное моделирование.
Системный анализ изучает структуру реальных объектов и дает способы их формализованного описания. Общая теория систем как часть системного анализа изучает различные по характеру системы с общих позиций.
Теория массового обслуживания изучает широкий класс моделей передачи и переработки информации в системах массового обслуживания (СМО).
Имитационное моделирование – наука, в которой создаются и используются специальные приемы воспроизведения процессов, протекающих в реальных объектах, в тех моделях этих объектов, которые реализуются в вычислительных машинах.
Теория принятия решений изучает общие схемы, используемые при выборе решения из альтернативных возможностей (в условиях неопределенности).
Теория игр изучает модели, в которых выбор происходит в условиях конфликта или противоборства.
Математическое программирование рассматривает проблемы принятия оптимальных решений с помощью математического аппарата.
Искусственный интеллект – одно из молодых и перспективных направлений информатики, появившееся во второй половине XX в. на базе вычислительной техники, математической логики, программирования, психологии, лингвистики и других отраслей знаний. Объектами его изучения являются межпредметные процедуры (метапроцедуры), используемые при решении задач, традиционно называемых интеллектуальными. Проникая в тайны творческой деятельности людей, искусственный интеллект создает программные и программно-аппаратные модели таких метапроцедур.
Информационные системы применяются для анализа и прогнозирования потока информации, исследования способов её представления, хранения и извлечения. Актуальным является также создание информационно-поисковых систем хранения, обработки, передачи информации, в состав которых входят информационные базы данных, терминалы, средства связи. Операционные системы связаны с разработкой и производством компьютеров.
Для нас представляют интерес все эти направления современной информатики. Теперь мы сможем осознать место дискретной математики в системе знаний, необходимых для тех, кто связал свою жизнь с компьютером.
Понятия «множества», «отношения», «функции» и другие, близкие к ним, составляют основной словарь дискретной математики. Рассматриваются конечные множества, а тонкие и сложные вопросы, связанные с бесконечными множествами, сознательно опущены.
Видео:КАК РАЗОБРАТЬСЯ В ВЫСШЕЙ МАТЕМАТИКЕСкачать
Глава 1. МНОЖЕСТВА И ОТНОШЕНИЯ
Видео:Все о векторах. 2 номер ЕГЭ по математике | Эрик ЛегионСкачать
1.1. Множества
Понятие множества принадлежит к числу фундаментальных неопределяемых понятий. Можно сказать, что множество – это любая определенная совокупность объектов. Объекты, из которых составлено множество, называют элементами. Элементы множества отличают друг от друга. Например, множество всех книг в библиотеке или множество вершин многоугольника.
Множества обозначаются большими буквами. Например, A, B, C, X, N и т. д. Если объект a является элементом множества A, то говорят, что a принадлежит A. Это записывается, как 
. Запись 
будет означать, что a не является элементом A.
Множества как объекты могут быть элементами других множеств. Множества, элементами которых являются другие множества, называются классом или семейством.
Множество, не содержащее элементов, называется пустым и обозначается 
.
Видео:Олегу Тинькову запрещён вход на Мехмат МГУСкачать
1.2. Задание множеств
Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать разными способами:
перечислением М элементов: 
;
характеристическим предикатом: 
;
порождающей процедурой: 
.
Перечисление задается в фигурных скобках, через запятую.
Здесь и далее фигурными скобками 
будем обозначать множество, в котором не играет роли порядок следования элементов, и круглыми скобками 
последовательность, в которой порядок следования элементов важен. Угловыми скобками 
будем обозначать совокупности элементов, имеющие неоднородную математическую природу (структуру), например, в графе имеем два вида элементов – вершины 
и дуги (пары) этих элементов ().
Характеристический предикат – это некоторое условие, выраженное в форме логического утверждения. Если для данного элемента условие выполнено, то оно принадлежит определённому множеству. В противном случае – не принадлежит.
Порождающая процедура – это процедура, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определённого множества.
Пример: 
.
.
Видео:Дискретная математика. ДНФСкачать
1.3. Операции над множествами
Множества удобно изображать с помощью кругов Эйлера (диаграмм Венна). Элементы множества изображаются точками внутри круга, если они принадлежат множеству ( 
на рис 1.1 а), и точками вне круга, если они множеству не принадлежат (
).
Рис. 1.1. Иллюстрация кругами Эйлера
Будем также использовать символы 
вместо слов «для любых х», «каждый элемент х» и 
вместо слов «существует х».
Множество A содержится во множестве B (множество B включает в себя множество A), если каждый элемент A принадлежит также и B (рис 1.1 б):
В этом случае A называется подмножеством B, а B – надмножеством A.
Если 
и 
, то A называется собственным подмножеством B.
Два множества равны, если они являются подмножествами друг друга, т. е.
.
Мощность множества обозначается как |М|. Для конечных множеств мощность – это число элементов. Например, 
, но 
.
Если А=В, то множества A и B называются равномощными.
Пример. Множество решений (корней) уравнения 
, т. е. 
. Множество простых чисел, меньших пяти 
. Следовательно, А=В.
Для некоторых числовых множеств приняты стандартные обозначения:
N – множество натуральных чисел 
;
Z – множество целых чисел 
;
Q – множество рациональных чисел 
;
R – множество действительных чисел;
C – множество комплексных чисел.
Тогда 
и т. д.
Если в множестве A найдется хотя бы один элемент, не принадлежащий B, то A не является подмножеством B, т. е. 
.
Например, интервал 
не является подмножеством промежутка 
, так как 
, но 
.
Из определения следует, что любое множество является подмножеством самого себя, т. е. справедливо утверждение 
. Полагают, что Æ является подмножеством любого множества.
Пример. Рассмотрим множество, состоящее из трех элементов: 
. Найдем все его подмножества:
а) пустое ;
б) по одному 
в) по два 
г) по три 
.
Число всех подмножеств составляет 8=23. Если множество состоит из n элементов, то число всех подмножеств равно 2n. Или булеан |2М|=2|М|.
Множество, состоящее из всех элементов, принадлежащих и множеству A, и множеству B, называется пересечением и обозначается 
.
.
Пример: 
.
Если же множества A и B не имеют общих элементов, то их пересечением является пустое множество, то есть 
. Например, пересечение множества четных чисел с множеством нечетных.
Пересечение пустого множества с любым множеством – пустое множество: 
.
1. Коммутативность (переместительное свойство). По аналогии с а+b=b+a
.
2. Ассоциативность. По аналогии с 
.
3. Свойство нуля. По аналогии с 
.
4. Идемпотентность (аналогии нет)
.
5. Дистрибутивность. По аналогии с 
; 
6. Свойство единицы.
Если задан универсум U и любые 
, то можно записать: 
(рис. 1.2 а); 
(рис. 1.2 б).
Множество, состоящее из всех элементов, принадлежащих или множеству A, или множеству B, называется объединением множеств. Обозначается так: 
.
Пример. Даны множества 
и 
. Их объединением будет 
.
Даны числовые промежутки (рис. 1.3). Их объединением будет 
.
Объединение и пересечение множеств хорошо иллюстрируются на плоскости (рис. 1.4). При этом множества изображаются кругами или прямоугольниками.
Свойства объединения множеств можно сравнить со свойствами сложения чисел. Проведем аналогию этих свойств.
1. Коммутативность (переместительное свойство). По аналогии с 
.
2. Ассоциативность. По аналогии с 
.
3. Свойство нуля. По аналогии с 
.
4. Идемпотентность (аналогии нет)
.
5. Дистрибутивность. По аналогии с 
.
Рис. 1.3. Множества точек отрезков
Рис. 1.4. Операции над множествами
Записывается так: 
.
Геометрическое представление разности множеств на рис. 1.5.
Симметричная разность (рис. 1.6):
;
.
Рис. 1.5. Разность множеств Рис. 1.6. Симметричная разность
Дополнение множеств (рис. 1.7):
;
.
Рис. 1.7. Дополнение
Свойства дополнения 
:
1) 
; 4) 
;
2) 
; 5) 
;
3) 
; 6) 
.
Пример. Рассмотрим операцию дополнения множества, являющегося пересечением множеств A и B. Её результат совпадает с объединением дополнений этих множеств, (свойство 6) 
; в этом можно убедиться с помощью диаграмм Эйлера – Венна (рис. 1.8).
Рис. 1.8. Геометрическая иллюстрация свойства 6
Декартово произведение множеств
Пусть A – конечное множество, состоящее из n элементов. Кортежем длины n элементов множества A называется упорядоченная последовательность (а1, а2, …, аn) элементов этого множества.
Например, равны кортежи ( )= , так как оба кортежа длины 5 и равны все пары соответствующих элементов данных множеств: 
, 
, 
, 
, 
.
Из двух данных кортежей (а1, а2, …, ai, …, аk), где 
, длины k и (b1, b2, …, bj, …, bm), где 
, длины m можно составить новый кортеж длиной 
, элементы которого (а1, а2, …, аk, b1, b2, …, bm) принадлежат множеству 
. Эта операция называется соединением кортежей. Кортеж можно образовать двумя способами, поэтому важно, какой кортеж назван первым. Так, соединив кортежи четных и нечетных однозначных чисел 
и 
, получим кортеж всех однозначных чисел 
.
Пусть A – конечное множество, элементами которого являются некоторые символы, например цифры, буквы, знаки препинания. Такие множества принято называть алфавитом над заданным множеством символов. Алфавит есть кортеж попарно различимых символов, называемых буквами алфавита. Элементы множества An принято называть словами длины n в алфавите A. Слово над алфавитом есть просто некоторая конечная последовательность символов. Так, шестизначный телефонный номер является словом длины 6 над алфавитом цифр 
.
Рассмотрим множество B, состоящее из двух элементов: 0 и 1. Кортежи длины m из этих элементов обозначим Bm. Тогда 
. Такие кортежи называют упорядоченными наборами или векторами. Они имеют широкое применение в дискретной математике.
Вектор из нулей и единиц можно рассматривать как двоичное представление натурального числа.
Вектор, состоящий из единиц и нулей, описывает состояние памяти вычислительных машин, причём память может содержать числа, тексты, команды и т. д.
Пусть заданы множества 
. Декартовым произведением этих множеств называется множество 
, состоящее из всех кортежей 
длины n, в которых 
, где 
. Поскольку для задания кортежа важен порядок, то порядок множителей важен и в декартовом произведении.
Например, декартовым произведением множеств 
и 
будет являться множество пар 
. Скобки для указания пар опускают там, где это не может привести к затруднениям: 
. Если множества А:= 
и В:= 
конечны, то их декартово произведение может быть представлено в общем виде таблицей из m столбцов и k строк (рис. 1.9).
💥 Видео
Дискретная математика. Видео 3. Полнота системы функций.Скачать
