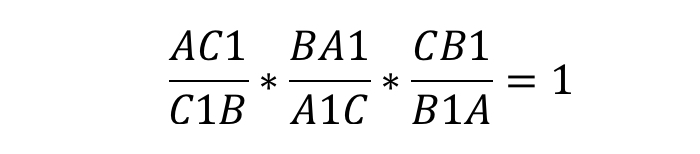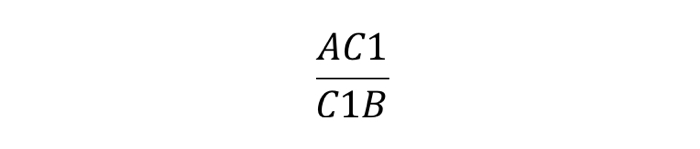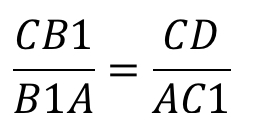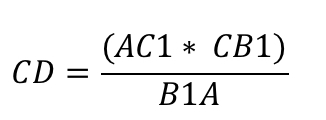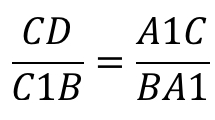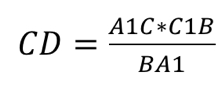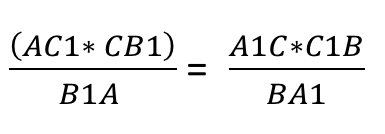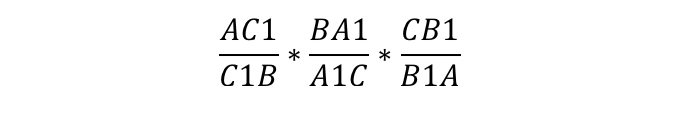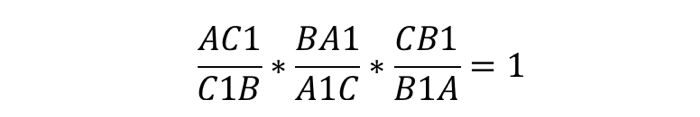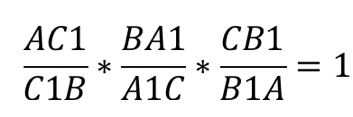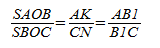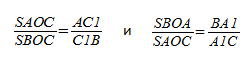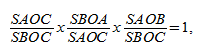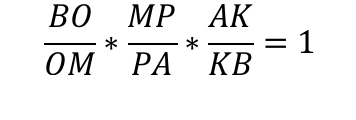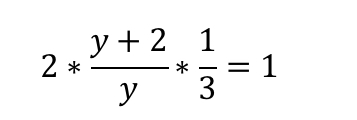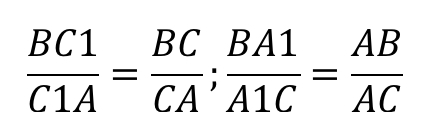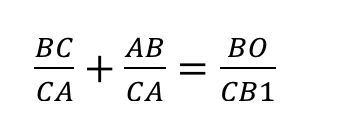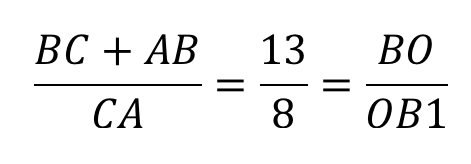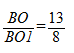- We are checking your browser. mathvox.ru
- Why do I have to complete a CAPTCHA?
- What can I do to prevent this in the future?
- Теорема Чевы и Менелая — формулировка, применение и примеры решения
- Формулировка теоремы Менелая
- Доказательство теоремы
- Формулировка теоремы Чевы
- Доказательство теоремы
- Применение теорем Чевы и Менелая при решении задач ЕГЭ
- Задача 1
- Задача 2
- Теоремы Чевы и Менелая на ЕГЭ
- 📺 Видео
Видео:✓ Теорема Чевы | Осторожно, спойлер! | Борис ТрушинСкачать

We are checking your browser. mathvox.ru
Видео:ЧевианаСкачать

Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:#189 ЧЕВИАНЫ // ТРЕУГОЛЬНИКСкачать

What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6d67379d2c9075bb • Your IP : 85.95.179.65 • Performance & security by Cloudflare
Видео:Чевиана в Московском пробнике по математике #егэ2023 #егэ #геометрия #чевианаСкачать

Теорема Чевы и Менелая — формулировка, применение и примеры решения
Теоремы Чевы и Менелая – одни из базовых основ планиметрии и геометрии, которым репетиторы и школьные учителя уделяют особое внимание, а ученикам задают писать научные доклады и рефераты на эту тему в качестве домашнего задания.
Их изучение рекомендуется не только в том случае, если вы – математик, но и в помощь ученикам старшего уровня (по уровню сложности может подойти и любой средний класс) и студентам профильных специальностей, которые всерьёз интересуются данной наукой.
Именно для этого мы подготовили данный материал. В нем вы узнаете, чем интересны данные основы, принципы их доказательств и рассмотрите решения некоторых задач из ЕГЭ.
Видео:Теорема Менелая | Математика | TutorOnlineСкачать

Формулировка теоремы Менелая
Менелай Александрийский — древнегреческий математик и астроном, живший в I в. Большой вклад внес в развитие сферической тригонометрии, где для получения формул использовал именно эту теорему, которую теперь изучают все школьники.
Прежде чем приступить к проработке, сделаем соответствующий рисунок.
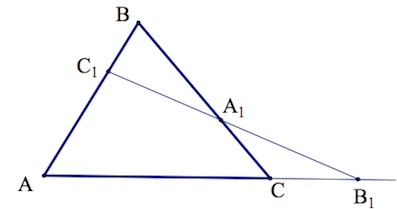
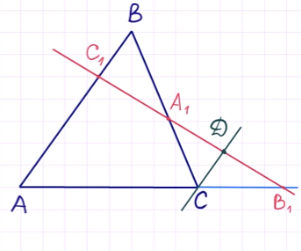
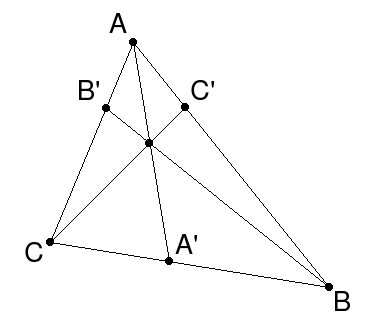
Что мы имеем? Треугольник ABC и прямую, которая пересекает две его стороны и продолжение третьей стороны.
Особенность теоремы заключается и в том, что приведённый рисунок чаще всего встречается в заданиях формата ЕГЭ. Это – весьма распространённая геометрическая конструкция, когда какая-то прямая таким образом пересекает треугольник.
Если мы видим приведённый выше рисунок, можно записать формулу:
Запомнить отношение просто: действуем по принципу «вершина — точка, точка — вершина». То есть, если на стороне AB нам дана некоторая точка C1, их отношенное записывается следующим образом:
Доказательство теоремы
Для доказательства теоремы Менелая проведём через точку C прямую, параллельную AB, таким образом:
Обозначим точку пересечения данной прямой с B1C1 через точку D.
В таком случае мы получим несколько пар подобных треугольников.
Сторона CD параллельна AB. Тогда первой парой подобных треугольников будут треугольники B1CD и B1AC1. Они подобны по второму признаку подобия треугольников, то есть по двум пропорциональным сторонам и углу B1 между ними.
Углы B1CD и B1AC1 равны как соответственные при параллельных прямых CD, AB и секущей AC.
Анализируя данную пару подобных треугольников, можно записать условие пропорциональности сходственных сторон, а именно:
Так как сторона CD не является составляющей исходного равенства, для дальнейшего доказательства её нужно выразить.
Используя описанное равенства, применив свойства пропорции, запишем:
Запишем следующую пару подобных треугольников: треугольники CDA1 и BC1A1 подобны, так как углы CA1D и BA1C1 равны как вертикальные. Кроме этого, угол CDA1 равен углу BC1A1, как накрест лежащие при параллельных прямых CD, AB и секущей C1D.
Покажем это на рисунке:
Из данного подобия можно записать некоторую пропорциональность сходственных сторон:
Так же выразим CD:
Осталось лишь приравнять. Дроби, с помощью которых мы выразили CD – равны.
Таким образом получаем:
Умножив обе дроби на часть, обратную левой дроби, мы получили исходное равенство:
Что и требовалось доказать.
Видео:Теорема ЧевыСкачать

Формулировка теоремы Чевы
Джованни Чева — итальянский математик, инженер. Годы жизни 1648 — 1734 гг. Основные труды ученого в области геометрии и механики.
Рассматриваемая теорема была доказана ученым в 1678 г.
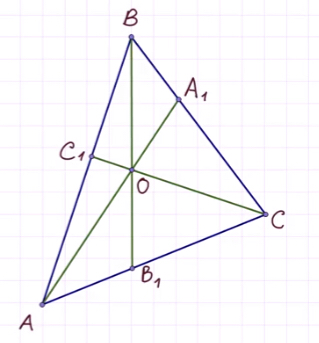
Рассмотрим приведённый ниже рисунок:
Теорема звучит так: любые произвольные отрезки, выходящие из вершин треугольника, (но с одним условием: они должны пересекаться в одной точке) делят противолежащие этим вершинам стороны таким образом, что истинно равенство:
В честь ученого, доказавшего эту теорему, данные отрезки называют «чевианами».
Доказательство теоремы
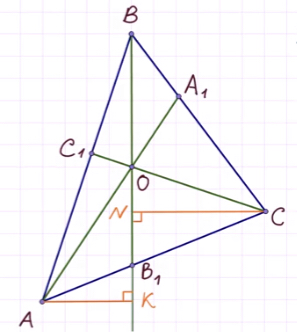
Итак, мы имеем треугольник ABC и произвольные чевианы AA1 и BB1.
Третья чевиана CC1 обязательно должна проходить через точку пересечения первых двух. При этом получается, что:
Обозначим за O точку пересечения данных прямых.
Продлим медиану BB1.
Проведём перпендикуляры из вершин A и С таким образом:
Треугольники AKB1 и CNB1 подобны по острому углу.
Теперь перемножим равенства:
что и требовалось доказать.
Видео:9 класс. Геометрия. Теорема Чевы.Скачать

Применение теорем Чевы и Менелая при решении задач ЕГЭ
Теорема Менелая (как и обратная) применима и в первой части экзаменационного бланка, и в 16-м задании. Рассмотрим пару таких задач.
Задача 1
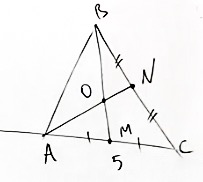
Дан треугольник ABC (см. рисунок ниже) с продолжением стороны CA. Также проведены медианы BM и AN. Точку их пересечения обозначим за O.
Возьмём точку K на стороне AB, такую, что AK относится к AB, как 1/3.
AC = 4 см, AM = 2 см.
Проведём прямую OK до пересечения со стороной AC. Точку их пересечения обозначим за P.
Сторону AP обозначим за y.
Найти: чему равен отрезок AP.
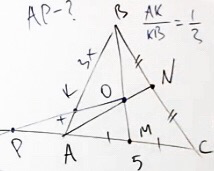
Так как отношение сторон AB и AK равно 1/3, следовательно, AK = x, а KB = 3x.
Рассмотрим треугольник ABM. Для него берём прямую OP.
Таким образом мы нашли искомые точки P, A, M, O, K и B.
Запишем теорему Менелая к данному рисунку.
Подставляем в это соотношение известные данные:
В итоге мы получаем, что y = 4.
Ответ: отрезок AP = 4 см.
Задача 2
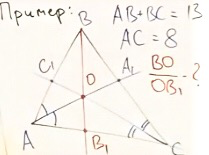
Задача, связанная со свойствами теоремы Чевы.
сумма AB и BC равна 13;
Найти: отношение BO и OB1.
Итак, запишем отношение:
Конечным результатом является дробь 13/8.
Видео:Математика-954. Чевиана и площади.Скачать

Теоремы Чевы и Менелая на ЕГЭ
Теоремы Чевы и Менелая на ЕГЭ
Подробная статья «Вокруг теорем Чевы и Менелая» опубликована на нашем сайте в разделе СТАТЬИ. Она адресована учителям математики и учащимся старших классов, мотивированным на хорошее знание математики. К ней можно вернуться, если появится желание подробнее разобраться в вопросе. В этой заметке мы приведем краткие сведения из упомянутой статьи и разберём решения задач из сборника для подготовки к ЕГЭ-2016.
Пусть дан треугольник ABC и на его сторонах AB, BC и AC отмечены точки C1, A1 и B1 соответственно (рис. 1).
а) Если отрезки AА1, BB1 и CС1 пересекаются в одной точке, то

б) Если верно равенство (1), то отрезки AА1, BB1 и CС1 пересекаются в одной точке.
На рисунке 1 изображен случай, когда отрезки AА1, BB1 и CС1 пересекаются в одной точке внутри треугольника. Это так называемый случай внутренней точки. Теорема Чевы справедлива и в случае внешней точки, когда одна из точек А1, B1 или С1 принадлежит стороне треугольника, а две другие — продолжениям сторон треугольника. В этом случае точка пересечения отрезков AА1, BB1 и CС1 лежит вне треугольника (рис. 2).
Как запомнить равенство Чевы?
Обратим внимание на прием запоминания равенства (1). Вершины треугольника в каждом отношении и сами отношения записываются в направлении обхода вершин треугольника ABC, начиная с точки A. От точки A идем к точке B, встречаем точку С1, записываем дробь 


Отметим, что любой отрезок, соединяющий вершину треугольника с любой точкой прямой, содержащей противоположную сторону треугольника, называют чевианой.
Рассмотрим несколько способов доказательства утверждения а) теоремы Чевы для случая внутренней точки. Чтобы доказать теорему Чевы, надо доказать утверждение а) любым из предложенных ниже способов, а также доказать утверждение б). Доказательство утверждения б) приведено после первого способа доказательства утверждения а). Доказательства теоремы Чевы для случая внешней точки проводятся аналогично.
Доказательство утверждения а) теоремы Чевы с помощью теоремы о пропорциональных отрезках
Пусть три чевианы AA1, BB1 и CC1 пересекаются в точке Z внутри треугольника ABC.
Идея доказательства заключается в том, чтобы отношения отрезков из равенства (1) заменить отношениями отрезков, лежащих на одной прямой.
Через точку В проведем прямую, параллельную чевиане СС1. Прямая АА1 пересекает построенную прямую в точке М, а прямая, проходящая через точку C и параллельная АА1, — в точке Т. Через точки А и С проведем прямые, параллельные чевиане ВВ1. Они пересекут прямую ВМ в точках N и R соответственно (рис. 3).




Тогда справедливы равенства

В параллелограммах ZСTM и ZСRВ отрезки TM, СZ и ВR равны как противоположные стороны параллелограмма. Следовательно, 

Утверждение а) теоремы Чевы доказано.
При доказательстве утверждения б) используем следующее утверждение. Рис. 3
Лемма 1. Если точки С1 и С2 делят отрезок AB внутренним (или внешним) образом в одном и том же отношении, считая от одной и той же точки, то эти точки совпадают.
Докажем лемму для случая, когда точки С1 и С2 делят отрезок AB внутренним образом в одном и том же отношении: 
Доказательство. Из равенства 


Доказательство леммы для случая, когда точки С1 и С2 делят отрезок AB внешним образом проводится аналогично.
Доказательство утверждения б) теоремы Чевы
Пусть теперь верно равенство (1). Докажем, что отрезки AА1, BB1 и CС1 пересекаются в одной точке.
Пусть чевианы АА1 и ВВ1 пересекаются в точке Z, проведем через эту точку отрезок CС2 (С2 лежит на отрезке AB). Тогда на основании утверждения а) получаем верное равенство



Можно доказать, что процедура записи равенства (1) не зависит, от того, от какой точки и в каком направлении совершается обход вершин треугольника.
Задание 1. Найдите длину отрезка АN на рисунке 4, на котором указаны длины других отрезков.
Задание 2. Чевианы AM, BN, CK пересекаются в одной точке внутри треугольника ABC. Найдите отношение 

Ответ. 
Доказательство утверждения а) с помощью подобия треугольников

Пусть прямые AA1, BB1, CC1 пересекаются в точке O внутри треугольника АВС (рис. 5). Через вершину С треугольника АВС проведем прямую, параллельную AB, и ее точки пересечения с прямыми AA1, BB1 обозначим соответственно A2, B2.
Из подобия двух пар треугольников CB2B1 и ABB1, BAA1 и CA2A1, Рис. 5


Из подобия треугольников BС1O и B2CO, AС1O и A2CO имеем равенства 


Утверждение а) теоремы Чевы доказано.
Рассмотрим доказательства утверждения а) теоремы Чевы с помощью площадей для внутренней точки. Оно изложено в книге [2] и опирается на утверждения, которые мы сформулируем в виде заданий 3 и 4.
Задание 3. Отношение площадей двух треугольников с общей вершиной и основаниями, лежащими на одной прямой, равно отношению длин этих оснований. Докажите это утверждение.
Задание 4. Докажите, что если 


Доказательство утверждения а) с помощью площадей
Пусть отрезки AА1, BB1 и CС1 пересекаются в точке Z (рис. 6), тогда








т. е. верно равенство (1), что и требовалось доказать.
Утверждение а) теоремы Чевы доказано.
Задание 15. Пусть чевианы пересекаются в одной точке внутри треугольника и разбивают его на 6 треугольников, площади которых равны S1, S2, S3, S4, S5, S6 (рис. 7). Докажите, что 
Задание 6. Найдите площадь S треугольника CNZ (площади других треугольников указаны на рисунке 8).
Задание 7. Найдите площадь S треугольника CNO, если площадь треугольника АNO равна 10 и 
Задание 8. Найдите площадь S треугольника CNO, если площадь треугольника АBC равна 88 и 










Так как 






Итак, 

Задание 9. В треугольнике ABC точки K и L принадлежат соответственно сторонам AB и BC. 

Пусть дан треугольник ABC и на его сторонах AC и CВ отмечены точки B1 и A1 соответственно, а на продолжении стороны AB отмечена точка C1 (рис. 11).
а) Если точки А1, B1 и С1 лежат на одной прямой, то

б) Если верно равенство (7), то точки А1, B1 и С1 лежат на одной прямой. Рис. 11
Как запомнить равенство Менелая?
Прием запоминания равенства (6) тот же, что и для равенства (1). Вершины треугольника в каждом отношении и сами отношения записываются в направлении обхода вершин треугольника ABC — от вершины к вершине, проходя через точки деления (внутренние или внешние).
Задание 10. Докажите, что при записи равенства (6) от любой вершины треугольника в любом направлении получается один и тот же результат.
Чтобы доказать теорему Менелая, надо доказать утверждение а) любым из предложенных ниже способов, а также доказать утверждение б). Доказательство утверждения б) приведено после первого способа доказательства утверждения а).
Доказательство утверждения а) с помощью теоремы о пропорциональных отрезках
I способ. а) Идея доказательства заключается в замене отношений длин отрезков в равенстве (6) отношениями длин отрезков, лежащих на одной прямой.
Пусть точки А1, B1 и С1 лежат на одной прямой. Через точку C проведем прямую l, параллельную прямой А1B1, она пересекает прямую АB в точке M (рис. 12).
 |
Рис. 12
По теореме о пропорциональных отрезках имеем: 

Тогда верны равенства 
Утверждение а) теоремы Менелая доказано.
Доказательство утверждения б) теоремы Менелая
Пусть теперь верно равенство (6), докажем, что точки А1, B1 и С1 лежат на одной прямой. Пусть прямые АB и А1B1 пересекаются в точке С2 (рис. 13).
Так как точки А1 B1 и С2 лежат на одной прямой, то по утверждению а) теоремы Менелая

Из сравнения равенств (6) и (7) имеем 



Последнее равенство верно лишь при условии 
Утверждение б) теоремы Менелая доказано. Рис. 13
Доказательство утверждения а) с помощью подобия треугольников
Идея доказательства заключается в том, чтобы заменить отношения длин отрезков из равенства (6) отношениями длин отрезков, лежащих на параллельных прямых.
Пусть точки А1, B1 и С1 лежат на одной прямой. Из точек A, B и C проведем перпендикуляры АА0, BB0 и СС0 к этой прямой (рис. 14).
 |
Рис. 14
Из подобия трех пар треугольников AA0B1 и CC0B1, CC0A1 и BB0A1, C1B0B и C1A0A (по двум углам) имеем верные равенства



перемножив их, получим:

Утверждение а) теоремы Менелая доказано.
Доказательство утверждения а) с помощью площадей
Идея доказательства заключается в замене отношения длин отрезков из равенства (7) отношениями площадей треугольников.
Пусть точки А1, B1 и С1 лежат на одной прямой. Соединим точки C и C1. Обозначим площади треугольников S1, S2, S3, S4, S5 (рис. 15).
Тогда справедливы равенства



Перемножив равенства (8), получим:

Утверждение а) теоремы Менелая доказано.
 |
Рис. 15
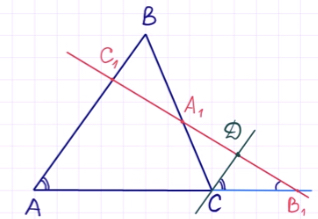
Подобно тому, как теорема Чевы остается справедливой и в том случае, если точка пересечения чевиан находится вне треугольника, теорема Менелая остается справедливой и в том случае, если секущая пересекает только продолжения сторон треугольника. В этом случае можно говорить о пересечении сторон треугольника во внешних точках.
Доказательство утверждения а) для случая внешних точек

По теореме о пропорциональных отрезках имеем:


Тогда верны равенства

Утверждение а) теоремы Менелая доказано. Рис. 16
Заметим, что приведенное доказательство совпадает с доказательством теоремы Менелая для случая, когда секущая пересекает две стороны треугольника во внутренних точках и одну во внешней.
Доказательство утверждения б) теоремы Менелая для случая внешних точек аналогично доказательству, приведенному выше.




Решение. Обозначим 




откуда следует, что

Ответ. 



Решение. Из точек Р и С опустим перпендикуляры PR и СМ на прямую АВ. Обозначим 






Из подобия треугольников КMC и КRP (по двум углам) получим, что 

Теперь, зная длину высоты, проведенной к стороне AB треугольника ABС, и площадь этого треугольника, вычислим длину стороны: 


Решение. Обозначим 




По теореме Менелая для треугольника BCY и секущей OX имеем: 

Ответ. 
Задание 14 (ЕГЭ-2016).
Точки В1 и С1 лежат на сторонах соответственно АС и АВ треугольника ABC, причём АВ1:B1С =
= АС1:С1B. Прямые ВВ1 и СС1 пересекаются в точке О.

б) Найдите отношение площади четырёхугольника AB1OC1 к площади треугольника ABC, если известно, что АВ1:B1С = 1:4. [8]
Решение. а) Пусть прямая AO пересекает сторону BC в точке A1 (рис. 20). По теореме Чевы имеем:

Так как АВ1:B1С = АС1:С1B, то из равенства (9) следует, что 
б) Пусть площадь треугольника AB1O равна S. Так как АВ1:B1С = 1:4, то площадь треугольника CB1O равна 4S, а площадь треугольника AOC равна 5S. Тогда площадь треугольника AOB тоже равна 5S, так как треугольники AOB и AOC имеют общее основание AO, а их вершины B и C равноудалены от прямой AO. Причём площадь треугольника AOC1 равна S, так как АС1:С1B = 1:4. Тогда площадь треугольника ABB1 равна 6S. Так как АВ1:B1С = 1:4, то площадь треугольника CB1O равна 24S, а площадь треугольника ABC равна 30S. Теперь найдём отношение площади четырёхугольника AB1OC1 (2S) к площади треугольника ABC (30S), оно равно 1:15.
Задание 15 (ЕГЭ-2016).
Точки В1 и С1 лежат на сторонах соответственно АС и АВ треугольника ABC, причём АВ1:B1С =
= АС1:С1B. Прямые ВВ1 и СС1 пересекаются в точке О.
а) Докажите, что прямая АО делит пополам сторону ВС.
б) Найдите отношение площади четырёхугольника AB1OC1 к площади треугольника ABC, если известно, что АВ1:B1С = 1:3. [8]

а) Докажите, что треугольник DCL равнобедренный.
б) Известно, что cos

Решение. а) Пусть углы при основании BC равнобедренного треугольника ABC (рис. 21) равны 








б) Пусть AK — медиана, проведённая к основанию BC равнобедренного треугольника ABC, она является высотой, поэтому BK:BA = cos


По теореме Менелая 


Задание 17 (ЕГЭ-2016). На отрезке BD взята точка С. Биссектриса BL равнобедренного треугольника ABC с основанием ВС является боковой стороной равнобедренного треугольника BLD с основанием BD.
а) Докажите, что треугольник DCL равнобедренный.
б) Известно, что cos

1. , Смирнов точки и линии треугольника. М.: Математика, 2006, № 17.
2. Мякишев геометрии треугольника. (Серия «Библиотека «Математическое просвещение»»). М.: МЦНМО, 2002. — 32 с.
3. Геометрия. Дополнительные главы к учебнику 8 класса: Учебное пособие для учащихся школ и классов с углубленным изучением / , , и др. — М.: Вита-Пресс, 2005. — 208 с.
4. Теоремы Чевы и Менелая. М.: Квант, 1990, № 3, С. 56–59.
5. Шарыгин Чевы и Менелая. М.: Квант, 1976, № 11, С. 22–30.
6. Вавилов и средние линии треугольника. М.: Математика, 2006, № 1.
7. Ефремов Дм. Новая геометрия треугольника. Одесса, 1902. — 334 с.
8. Математика. 50 вариантов типовых тестовых заданий / , , и др.; под ред. . – М.: Издательство «Экзамен», 2016. — 247 с.
📺 Видео
ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Он вам не Чева. Теорему забанили на ЕГЭ 2022 по математике. Доказательство теоремы ЧевыСкачать

Вебинар 4. Планиметрия. Теоремы Менелая и Чевы в действииСкачать

Теорема о медианеСкачать
Теорема ЧевыСкачать

Треугольник и теорема ЧевыСкачать

Теорема о трёх медианахСкачать

Теорема Чевы. Часть 2. | ГеометрияСкачать

69 Две чевианыСкачать

11 класс, 51 урок, Теорема ЧевыСкачать

Геометрия: теоремы Менелая, Чевы | Профильная математика ЕГЭ 2023 | УмскулСкачать

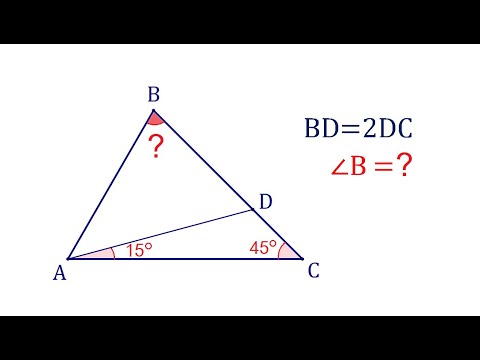
Олимпиадная задача за 2 минуты ➜ Найдите уголСкачать