Длина вектора в maple (3 видео) | Курс школьной геометрии

Длина вектора в maple

Основная часть команд для решения задач линейной алгебры содержится в библиотеке linalg . Поэтому перед решением задач с матрицами и векторами следует загрузить эту библиотеку командой with(linalg) .

Способы задания векторов.

Для определения вектора в Maple используется команда vector([x1,x2,…,xn]), где в квадратных скобках через запятую указываются координаты вектора. Например:

Координату уже определенного вектора x можно получить в строке вывода, если ввести команду x[i] , где i — номер координаты. Например, первую координату заданного в предыдущем примере вектора можно вывести так:

Вектор можно преобразовать в список и, наоборот, с помощью команды convert(vector, list) или convert(list, vector).

Сложить два вектора a и b можно с помощью двух команд:

Команда add позволяет вычислять линейную комбинацию векторов a и b : , где — скалярные величины, если использовать формат: matadd(a,b,alpha,beta) .

Скалярное, векторное произведение векторов и угол между векторами.

Скалярное произведение двух векторов вычисляется командой dotprod(a,b).

Векторное произведение двух векторов вычисляется командой crossprod(a,b).

Угол между двумя векторами a и b вычисляется с помощью команды angle(a,b) .

Норму (длину) вектора , которая равна , можно вычислить с помощью команды norm(а,2) .

Можно нормировать вектор а с помощью команды normalize(a), в результате выполнения которой будет получен вектор единичной длины .

Нахождение базиса системы векторов. Ортогонализация системы векторов по процедуре Грамма-Шмидта.

Если имеется система n векторов , то с помощью команды basis([a1,a2,…,an]) можно найти базис этой системы.

При помощи команды GramSchmidt([a1,a2,…,an]) можно ортогонализовать систему линейно-независимых векторов .

Содержание

Задание 1.
Пакеты линейной алгебры и функциональных систем
5. Функции для работы, с векторами и матрицами
🎦 Видео

Видео:Длина вектора через координаты. 9 класс.Скачать

Задание 1.

1. Даны два вектора: и . Найти и угол между a и b . Для решения этой задачи наберите:

2. Найти векторное произведение , а затем скалярное произведение , где , .

3. Найти норму вектора .

4. Из системы векторов: , , , , выделить базис и ортогонализовать его по процедуре Грамма-Шмидта:

g := [ a1, a2, a3, a5 ]

[[1,2,2, — 1], [2,3, — 3,2], ,

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Пакеты линейной алгебры и функциональных систем

Прежде чем перейти к рассмотрению обширных возможностей пакетов Maple 7 по части решения задач линейной алгебры, рассмотрим краткие определения, относящиеся к ней.

Матрица (m х n) — прямоугольная двумерная таблица, содержащая m строк и n столбцов элементов, каждый из которых может быть представлен числом, константой, переменной, символьным или математическим выражением (расширительная трактовка матрицы).

Квадратная матрица — матрица, у которой число строк m равно числу столбцов n . Пример квадратной матрицы размера 3×3:

Сингулярная (вырожденная) матрица — квадратная матрица, у которой детерминант (определитель) равен 0. Такая матрица обычно не упрощается при символьных вычислениях. Линейные уравнения с почти сингулярными матрицами могут давать большие погрешности при решении.

Единичная матрица — это квадратная матрица, у которой диагональные элементы равны 1, а остальные элементы равны 0. Ниже представлена единичная матрица размера 4×4:

Сингулярные значения матрицы А — квадратные корни из собственных значений матрицы А Т =А, где А т — транспонированная матрица А (см. ее определение ниже);Транспонированная матрица — матрица, у которой .столбцы и строки меняются . местами, то есть элементы транспонированной матрицы удовлетворяют условию A T (i,j)=A(j,i). Приведем простой пример. Исходная матрица:

Обратная матрица — это матрица М -1 , которая, будучи умноженной на исходную квадратную матрицу М, дает единичную матрицу Е.

Ступенчатая форма матрицы соответствует условиям, когда первый ненулевой элемент в каждой строке есть 1 и первый ненулевой элемент каждой строки появляется справа от первого ненулевого элемента в предыдущей строке, то есть все элементы ниже первого ненулевого в строке — нули.

Диагональ матрицы — расположенные диагонально элементы A i,i матрицы А. В приведенной ниже матрице элементы диагонали представлены заглавными буквами:

Обычно указанную диагональ называют главной диагональю — для матрицы А, приведенной выше, это диагональ с элементами А, Е и L. Иногда вводят понятия под диагоналей (элементы d и k) и над диагоналей (элементы b и f). Матрица, все элементы которой, расположенные кроме как на диагонали, под диагонали и над диагонали, равны нулю, называется ленточной.

Ранг матрицы — наибольший из порядков отличных от нуля миноров квадратной матрицы.

След матрицы — сумма диагональных элементов матрицы.

Определитель матрицы — это многочлен от элементов квадратной матрицы, каждый член которого является произведением n элементов, взятых по одному из каждой строки и каждого столбца со знаком произведения, заданным четностью перестановок:

где M 1 — определитель матрицы порядка n — 1, полученной из матрицы А вычеркиванием первой строки и j-гo столбца. В таком виде определитель (он же детерминант) легко получить в символьных вычислениях. В численных расчетах мы будем подразумевать под определителем численное значение этого многочлена.

Матрица в целой степени — квадратная матрица в степени n (n — целое неотрицательное число), определяемая следующим образом:

М° = Е, М 1 = М, М 2 = ММ . М n =М n-1 М.

Идемпотентная матрица — матрица, отвечающая условию Р 2 = Р.

Симметрическая матрица — матрица, отвечающая условию А т = А.

Кососимметрическая матрица — матрица, отвечающая условию А т = -A. Ортогональная матрица — матрица, отвечающая условию А т =А -1 .Нуль-матрица — матрица, все элементы которой равны 0.Блок-матрица — матрица, составленная из меньших по размеру матриц, также можно представить как матрицу, каждый элемент которой — матрица. Частным случаем является блок-диагональная матрица — блок-матрица, элементы-матрицы которой вне диагонали — нуль-матрицы.

Комплексно-сопряженная матрица — матрица А, полученная из исходной матрицы А заменой ее элементов на комплексно-сопряженные. Эрмитова матрица — матрица А, удовлетворяющая условию А = А .Собственный вектор квадратной матрицы А — любой вектор х е V», х* О, удовлетворяющий уравнению Ах = gx, где g — некоторое число, называемое собственным значением матрицы А.

Характеристический многочлен матрицы — определитель разности этой матрицы и единичной матрицы, умноженный на переменную многочлена, — |А — gE|. Собственные значения матрицы — корни ее характеристического многочлена. Норма — обобщенное понятие абсолютной (величины числа. Норма трехмерного вектора ||х|| — его длина. Норма матрицы — значение sup(||Ax||/||x||).

Матричная форма записи системы линейных уравнений — выражение АХ = В, где А — матрица коэффициентов системы, X — вектор неизвестных и В — вектор свободных членов. Один из способов решения такой системы очевиден — X = А -1 В, где А -1 — обратная матрица.

Пакет решения задач линейной алгебры linalg

Состав пакета linalg

Несомненно, что уникальной возможностью системы Maple 7, как и других систем компьютерной алгебры, является возможность решения задач линейной алгебры в символьном (формульном, аналитическом) виде. Однако такое решение представляет скорее теоретический, чем практический интерес, поскольку даже при небольших размерах матриц (уже при 4-5 строках и столбцах) символьные результаты оказываются очень громоздкими и труднообозримыми. Они полезны только при решении специфических аналитических задач, например с разреженными матрицами, у которых большинство элементов имеют нулевые значения.

Поэтому разработчики Maple 7 были вынуждены реализовать в своей системе численные методы решения задач линейной алгебры, которые широко используются в основных сферах ее приложения — математическом моделировании систем и устройств, расчетах в электротехнике, механике, астрономии и т. д.

В ядро Maple 7, как отмечалось, введены очень скромные и минимально необходимые средства для решения задач линейной алгебры. Основной упор в их реализации сделан на подключаемые пакеты. Основным из них, унаследованным от предшествующих реализаций системы, является пакет решения задач линейной алгебры Unalg. Это один из самых обширных и мощных пакетов в области решения задач линейной алгебры. Он содержит свыше ста функций:

Warning, the names fibonacci, inverse and multiply have been redefined Warning, the protected names norm and trace have been redefined and unprotected[BlockDiagonal, GramSchmidt, JordanBlock, LUdecomp, QRdecomp, Wronskian, addcol, addrow, adj, adjoint, angle, augment, backsub, band, basis, bezout, blockmatrix, charmat, charpoly, cholesky, col, coldim, colspace, colspan, companion, concat, cond, copyinto, crossprod, curl, definite, delcols, delrows, det, diag, diverge, dotprod, eigenvals, eigenvalues, eigenvectors, eigenvects, entermatrix, equal, exponential, extend, ffgausselimfifibonacci,forwardsub,frobenius, gausselim, gaussjord, geneqns, genmatrix, grad, hadamard, hermite, hessian, hilbert,htranspose, thermite, indexfunc, innerprod, intbasis, inverse, ismith, issimilar, iszerojacobian, Jordan, kernel, laplacian, leastsqrs, linsolve,matadd, matrix, minor, minpoly, mulcol, /им/row,multiply, norm, normalize, nullspace, orthog, permanent, pivot, potential, randmatrix, randvector, rank, ratform, row, rowdim, rowspace, rowspan, rref, scalarmul, singularvals, smith, stackmatrix, submatrix, subvector, sumbasis, swapcol, swaprow, Sylvester, toeplitz, trace, transpose, vandermonde, vecpotent, vectdim, vector, wronskian]

Ниже указано назначение тех функций пакета linalg , которые подробно не описаны:

addcol — добавляет к одному из столбцов другой столбец, умноженный на некоторое число;
addrow — добавляет к одной из строк другую строку, умноженную на некоторое число;
angle — вычисляет угол между векторами;
augment — объединяет две или больше матриц по горизонтали;
backsub — реализует метод обратной подстановки при решении системы линейных уравнений (см. также forwardsub );
band — создает ленточную матрицу;
basis — находит базис векторного пространства;
bezout — создает Bezout-матрицу двух полиномов; . г
BlockDiagonal — создает блок-диагональную матрицу;
blockmatrix — создает блок-матрицу;
cholesky — декомпозиция Холесского для квадратной положительно определенной матрицы;
charmat — создает характеристическую матрицу ( charmat (M,v) — матрица, вычисляемая как v E-M);
charpoly — возвращает характеристический полином матрицы;
colspace — вычисляет базис пространства столбцов;
colspan — находит базис линейной оболочки столбцов матрицы;
companion — вычисляет сопровождающую матрицу, ассоциированную с полиномом;
cond — вычисляет число обусловленности матрицы (cond(M) есть величина norm(M) norm (М -1 );
curl — вычисляет ротор вектора;
definite — тест на положительную (отрицательную) определенность матрицы;
diag — создает блок-диагональную матрицу;
diverge — вычисляет дивергенцию векторной функции;
eigenvals — вычисляет собственные значения матрицы;
eigenvects — вычисляет собственные векторы матрицы;
equal — определяет, являются ли две матрицы равными;
exponential — создает экспоненциальную матрицу;
ffgausselim — свободное от дробей Гауссово исключение в матрице;
fibonacci — матрица Фибоначчи;
forwardsub — реализует метод прямой подстановки при решении системы линейных уравнений (например, для матрицы L и вектора b
forwardsub(L, b) возвращает вектор решения х системы линейных уравнений L-x=b);
frobenius — вычисляет форму Фробениуса ( Frobenius ) матрицы;
gausselim — Гауссово исключение в матрице;
gaussjord — синоним для rref (метод исключения Гаусса—Жордана);
geneqns — генерирует элементы матрицы из уравнений;
genmatrix — генерирует матрицу из коэффициентов уравнений;
grad — градиент векторного выражения;
GramSchmidt — вычисляет ортогональные векторы;
hadamard — вычисляет ограничение на коэффициенты детерминанта;
hessian — вычисляет гессиан-матрицу выражения;
hilbert — создает матрицу Гильберта;
htranspose — находит эрмитову транспонированную матрицу;
ihermite — целочисленная эрмитова нормальная форма;
indexfunc — определяет функцию индексации массива;
Innerprod — вычисляет векторное произведение;
Intbasis — определяет базис пересечения пространств;
ismith — целочисленная нормальная форма Шмитта;
iszero — проверяет, является ли матрица ноль-матрицей;
jacobian —’ вычисляет якобиан векторной функции;
JordanBlock — возвращает блок-матрицу Жордана;
kernel — находит базис ядра преобразования, соответствующего данной матрице;
laplacian — вычисляет лапласиан;
leastsqrs — решение уравнений по методу наименьших квадратов;
linsolve — решение линейных уравнений;
LudeComp — осуществляет LU-разложение;
minpoly — вычисляет минимальный полином матрицы;
mulcol — умножает столбец матрицы на заданное выражение;
mulrow — умножает строку матрицы на заданное выражение;
multiply — перемножение ‘матриц или матрицы и вектора;
normalize — нормализация вектора;
orthog — тест на ортогональность матрицы;
permanent — вычисляет перманент матрицы — определитель, вычисляемый без перестановок;
pivot — вращение относительно элементов матрицы;
potential — вычисляет потенциал векторного поля;
Qrdecomp — осуществляет QR-разложение;
randmatrix — генерирует случайные матрицы;
randvector — генерирует случайные векторы;
ratform — вычисляет рациональную каноническую форму;
references — выводит список основополагающих работ по линейной алгебре;
rowspace — вычисляет базис пространства строки;
rowspan — вычисляет векторы охвата для места столбца;
rref — реализует преобразование Гаусса-Жордана матрицы;
scalarmul — умножение матрицы или вектора на заданное выражение;
singval — вычисляет сингулярное значение квадратной матрицы;
singularvals — возвращает список сингулярных значений квадратной матрицы;
smith — вычисляет Шмиттову нормальную форму матрицы;
submatrix — извлекает указанную подматрицу из матрицы;
subvector — извлекает указанный вектор из матрицы;
sumbasis — определяет базис объединения системы векторов;
swapcol — меняет местами два столбца в матрице;
swaprow — меняет местами две строки в матрице;
sylvester — создает матрицу Сильвестра из двух полиномов;
toeplitz — создает матрицу Теплица;
trace — возвращает след матрицы;
vandermonde — создает вандермондову матрицу;
vecpotent — вычисляет векторный потенциал;
vectdim — определяет размерность вектора;
wronskian — вронскиан векторных функций.

Ниже мы рассмотрим более подробно наиболее часто используемые функции из этого пакета. С деталями синтаксиса (достаточно разнообразного) для каждой из указанных функций можно ознакомиться в справочной системе Maple. Для этого достаточно использовать команду

?name ; где name — имя функции (из приведенного списка).

Интерактивный ввод матриц

Для интерактивного ввода матриц можно, определив размерность некоторого массива, использовать функцию entermatrix :

После исполнения этого фрагмента документа диалог с пользователем имеет следующий вид:

Видео:Модуль вектора. Длина вектора.Скачать

5. Функции для работы, с векторами и матрицами

Функции для работы с векторами и матрицами

Для работы с векторами и матрицами Maple 7 имеет множество функций, входящих в пакет linalg. Ограничимся приведением краткого описания наиболее распространенных функций этой категории.

Операции со структурой отдельного вектора V и матрицы М:

coldim(M) — возвращает число столбцов матрицы М;
rowdim(M) — возвращает число строк матрицы М;
vectdim(V) — возвращает размерность вектора V;
col(M,i) — возвращает i-й столбец матрицы М;
row(M,i) — возвращает i-ю строку матрицы М;
tninor(M,i, j) — возвращает минор матрицы М для элемента с индексами i и j;
delcols(M,i.. j) — удаляет столбцы матрицы М от i-roдо j-ro;
del rows (V,i..j) — удаляет строки матрицы М от i-й до j-й;
extend (М, т, n,х) — расширяет матрицу М на m строк и n столбцов с применением заполнителя х.

Основные векторные и матричные операции:

dotprod(U,V) — возвращает скалярное произведение векторов U и V;
crossprod(U,V) — возвращает векторное произведение векторов U и V;
norm(V) или norm(M) — возвращает норму вектора или матрицы;
copyinto(A,B,i, j) — копирует матрицу А в В для элементов последовательно от i до j;
concat(Ml,M2) — возвращает объединенную матрицу с горизонтальным слиянием матриц Ml и М2;
stack(Ml,M2) — возвращает объединенную матрицу с вертикальным слиянием Ml и М2;
matadd(A,B) и evalm(A+B) — возвращает сумму матриц А и В;
multlply(A,B) и evalm(A&*B) — возвращает произведение матриц А и В;
adjoint (М) или adj(M) — возвращает присоединенную матрицу, такую что M?adj(M) дает диагональную матрицу, определитель которой есть det(M);
charpoly(M,lambda) — возвращает характеристический полином матрицы М относительно заданной переменной lambda;
det(M) — возвращает детерминант (определитель) матрицы М;
Eigenvals(M,vector) — инертная форма функции, возвращающей собственные значения матрицы М и (при указании необязательного параметра vector) соответствующие им собственные векторы;
jordan(M) — возвращает матрицу М в форме Жордана;
hermite(M) — возвращает матрицу М в эрмитовой форме;
trace(M) — возвращает след матрицы М;
rank(M) — возвращает ранг матрицы М;
transpose(M) — возвращает транспонированную матрицу М;
inverse(M) или evalm(l/M) — возвращает матрицу, обратную к М;
singularvals(A) — возвращает сингулярные значения массива или матрицы А.

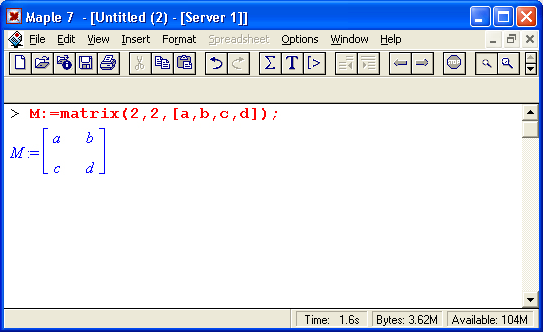
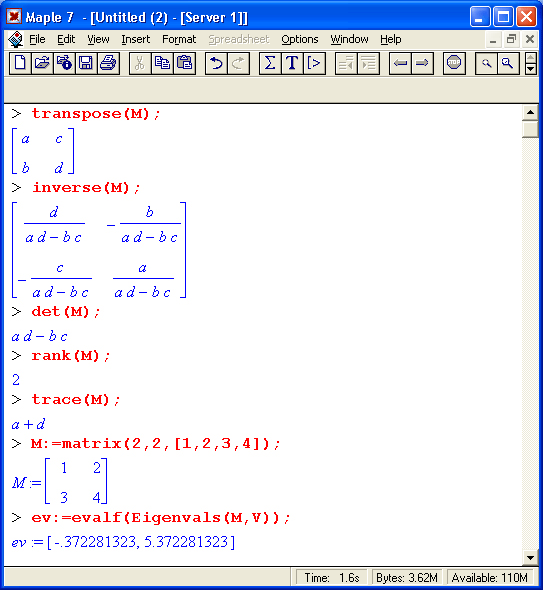
Приведем примеры применения некоторых из этих функций:

Читатель, понимающий суть матричных вычислений, легко справится с тестированием других функций, входящих в пакет linalg. В приведенных примерах полезно обратить внимание на то, что многие матричные функции способны выдавать результаты вычислений в аналитическом виде, что облегчает разбор выполняемых ими операций.