Четырёхугольник вписан в окружность (задачи). Продолжаем рассматривать задания входящие в состав ЕГЭ по математике. В этой статье мы решим несколько задач с использованием свойств вписанного угла. Теория была подробно уже изложена, обязательно посмотрите . В указанной статье решение заданий по сути сводилось к применению свойства вписанного угла сразу же, то есть это были задания практически в одно действие. Здесь нужно чуть подумать, ход решения не всегда с ходу очевиден.
Применяются: теорема о сумме углов треугольника, свойства вписанного угла, свойство четырёхугольника вписанного в окружность. О последнем подробнее.
*Это свойство было уже представлено, но в другой интерпретации. Итак:
Вписанный четырехугольник — это четырехугольник, все вершины которого лежат на одной окружности.
Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равны 180 градусам.
То есть, если мы такой четырёхугольник, то сумма его противоположных углов равна 180 градусам.
27870. В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 110 0 . Найдите вписанный угол ACB. Ответ дайте в градусах.
Треугольник BОC равнобедренный, так как ОС=ОВ (это радиусы). Известно, что сумма углов треугольника равна 180 градусам. Рассмотрим ∠BOC и ∠AOD:
Углы при основании равнобедренного треугольника равны, то есть
Угол АОВ является центральным углом для вписанного угла АСВ. По свойству вписанного в окружность угла
Сумма смежных углов равна 180 0 , значит
27871. Угол А четырехугольника ABCD, вписанного в окружность, равен 58 0 . Найдите угол C этого четырехугольника. Ответ дайте в градусах.
Здесь достаточно вспомнить свойство такого четырёхугольника. Известно, что сумма его противоположных углов такого равна 180 градусам, значит угол С будет равен
Построим ОВ и OD.
По свойству вписанного угла градусная величина дуги BCD равна
Следовательно градусная величина дуги BAD будет равна
360 0 – 116 0 = 244 0
По свойству вписанного угла угол С будет в два раза меньше, то есть 122 0 .
27872. Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95 0 , 49 0 , 71 0 , 145 0 . Найдите угол B этого четырехугольника. Ответ дайте в градусах.
Построим радиусы АО, OD, OC:
Градусная величина дуги AD равна 145 0 , градусная величина дуги СD равна 71 0 , значит градусная величина дуги АDС равна 145 0 + 71 0 = 216 0 .
По свойству вписанного угла угол В будет в два раза меньше центрального угла соответствующего дуге АDС, то есть
27874. Четырехугольник ABCD вписан в окружность. Угол ABC равен 105 0 , угол CAD равен 35 0 . Найдите угол ABD. Ответ дайте в градусах.
Данная задача может вызвать затруднение. Сразу невозможно явно увидеть ход решения. Вспомним, что известно про вписанный четырёхугольник: сумма его противоположных углов равна 180 градусам. Найдём
На данный момент мы нашли тот угол, который сразу же возможно определить по известному свойству. Если есть возможность найти какую-либо величину, сделайте это, пригодится. Действуем по принципу «находим то, что можно найти исходя из данных величин».
Далее используя теорему о сумме углов треугольника найдём угол ACD:
Вписанные углы ABD и ACD опираются на одну и туже дугу, это означает, что они равны, то есть
27875. Четырехугольник ABCD вписан в окружность. Угол ABD равен 75 0 , угол CAD равен 35 0 . Найдите угол ABC. Ответ дайте в градусах.
Известно, что вписанные углы опирающиеся на одну и ту же дугу, и лежащие от неё по одну сторону равны. Следовательно
В треугольнике ACD известно два угла, можем найти третий:
Далее воспользуемся свойством – известно, что у вписанного в окружность четырехугольника сумма противолежащих углов равна 180 0 , значит
27869. AC и BD — диаметры окружности с центром O. Угол ACB равен 38 0 . Найдите угол AOD. Ответ дайте в градусах.
27873. Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как 4:2:3:6. Найдите угол A четырехугольника ABCD. Ответ дайте в градусах.
27876. Четырехугольник ABCD вписан в окружность. Угол ABC равен 110 0 , угол ABD равен 70 0 . Найдите угол CAD. Ответ дайте в градусах.
Отмечу, что важно помнить указанные свойства и задачи вы решите без проблем. Конечно, можно выстроить решение не совсем корректно. Например, в задаче 27876 для самостоятельного решения приведено «длинное», или как ещё говорят нерациональное решение. Ничего страшного, если вы именно также решите задачу.
Главное чтобы вы помнили и применяли теорию, и в конечном итоге РЕШИЛИ задание.
В данной рубрике продолжим рассматривать задачи, приглашаю вас на блог!
На этом всё. Успеха вам!
С уважением, Александр Крутицких
Комиссия спрашивает у директора простой сельской школы:
— По какой причине у вас все дети говорят: пришедши, ушедши?
— А кто их знает, может они так привыкши!
- Решение вписанные и описанные четырехугольники для ОГЭ и ЕГЭ методическая разработка по геометрии (9 класс) на тему
- Скачать:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- Задачи на вписанные четырехугольники в окружность
- Решение вписанные и описанные четырехугольники для ОГЭ и ЕГЭ методическая разработка по геометрии (9 класс) на тему
- Скачать:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- Четырёхугольник вписан в окружность
- Дидактический материал по теме «Вписанные в окружность четырехугольники. Описанные около окружности четырехугольники.»
- Просмотр содержимого документа «Дидактический материал по теме «Вписанные в окружность четырехугольники. Описанные около окружности четырехугольники.»»
- 💡 Видео
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Решение вписанные и описанные четырехугольники для ОГЭ и ЕГЭ
методическая разработка по геометрии (9 класс) на тему
Предложены решения задач из баннка данных для ОГЭ и ЕГЭ. Удобно использовать для коррекции знаний или для учащихся, пропустивших занятия по подготовке к итоговой атттестации
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Скачать:
| Вложение | Размер |
|---|---|
| reshenie_vpis_i_opis_chetyrehugolniki_ege_i_oge_.doc | 386 КБ |
Видео:Четырехугольники, вписанные в окружность. 9 класс.Скачать

Предварительный просмотр:
Окружность, вписанная в многоугольни к http://egemaximum.ru/zadachi-7-mnogougolnik-i-okruzhnost/
Задача 1 . Найдите радиус окружности, вписанной в квадрат со стороной 16.
Решение: Радиус вписанной окружности в квадрат – есть половина стороны квадрата. Поэтому r = 8
Задача 2 . Сторона ромба равна 58, острый угол равен 30˚. Найдите радиус вписанной окружности этого ромба.
Решение: Пусть точки касания окружности противоположных сторон ромба – E и T. Тогда ET– диаметр окружности (точка пересечения диагоналей О – центр симметрии параллелограмма, значит и ромба).
ET – есть расстояние между противоположными сторонами ромба так же, как и высота ромба (DH).
Рассмотрим прямоугольный треугольник ADH. Так как угол А равен 30°по условию, то катет HD, противолежащий этому углу, равен половине гипотенузы AD. То есть HD=ET=29. Значит, радиус вписанной окружности есть ET: 2, то есть 14,5. Ответ: 14,5.
Задача 3 . Найдите высоту трапеции, в которую вписана окружность радиуса 14.
Решение: Высота трапеции – есть диаметр вписанной окружности в трапецию.
h=2r=2·14, h = 28. Ответ:28
Задача 4. Боковые стороны трапеции, описанной около окружности, равны 19 и 13. Найдите среднюю линию трапеции.
Решение: в трапецию вписана окружность, значит BC+AD=AB+CD, что хорошо видно на картинке (равные отрезки помечены согласно свойству отрезков касательных).Итак, BC+AD=32, средняя линия l – есть полусумма оснований, то l =16.
Задача 5. Периметр прямоугольной трапеции, описанной около окружности, равен 80, ее большая боковая сторона равна 30. Найдите радиус окружности
Решение: в трапецию вписана окружность, значит BC+AD=AB+CD и P ABCD =80, то AB+CD= P:2 = 40. CD=30 по условию, то AB=10.
Далее, AB=NQ=2r. r =5. Ответ:5
Задача 6. В четырехугольник ABCD вписана окружность, AB=52, CD=53. Найдите периметр четырехугольника.
Решение: Раз в выпуклый четырехугольник ABCD вписана окружность, то AB+CD=BC+AD. P ABCD =2(AB+CD)=2(52+53)=210
Задача 7 . Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1:17:23 . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 84.
Решение: В выпуклый четырехугольник ABCD вписана окружность, значит AB+CD=BC+AD. По условию три стороны четырехугольника относятся как 1:17:23, пусть тогда AD=x;AB=17x; BC=23x. Итого, 24x=17x+CD; 7x=CD;
Наконец, так как по условию периметр четырехугольника равен 84, то 24x=42;
x= 7/4.Очевидно, большая сторона – это BC=23x. BC=23·(7/4) = 40,25.
Задача 8 . Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
Решение: Сторона квадрата вдвое больше радиуса вписанной в него окружности. Поэтому сторона квадрата равна . Радиус описанной вокруг квадрата окружности равен половине его диагонали. Поэтому радиус описанной окружности есть . Ответ: 6.
Задача 9 . Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен
Решение: Шестиугольник составлен из 6 правильных треугольников. Рассмотрим правильный треугольник AOF: В нем OH = r – медиана и высота, , , тогда , АО=66 Ответ: 66.
Окружность, описанная около многоугольни к http://egemaximum.ru/zadachi-7-mnogougolnik-i-okruzhnost/
Задача 1 . Угол A четырехугольника ABCD, вписанного в окружность, равен 26˚. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
Решение: Вписанный в окружность угол A опирается на дугу BCD, значит дуга BCD=52° по свойству вписанного угла. Дуга BAD, дополняющая дугу BCD до окружности, равна 360°-52°=308°. Тогда угол Cравен 308°: 2 = 154°. Ответ: 154.
Задача 2. Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 78˚, 107˚, 39˚, 136˚. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
Решение: Вписанный угол C опирается на дугу BAD, равную 78˚+136˚=214˚.
Значит сам угол равен 214 : 2 = 107˚. Ответ: 107.
Задача 3 . Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как 1:2:7:26. Найдите угол A четырехугольника ABCD. Ответ дайте в градусах.
Решение: Дуги AB,BC,CD,AD в сумме составляют 360˚. Так как градусные меры дуг AB, BC, CD и AD относятся соответственно как 1:2:7:26, то пусть AB=x, BC=2x, CD=7x,AD=26x градусов. Имеем, x+2x+7x+26x=360;36x=360;x=10. Угол A опирается на дугу BD=9x градусов, значит угол A равен 90˚: 2 = 45˚. Ответ: 45 .
Задача 4 . Четырехугольник ABCD вписан в окружность. Угол ABC равен 38˚, угол CAD равен 33˚. Найдите угол ABD. Ответ дайте в градусах.
Решение : ABC=38˚, значит дуга ADC равна 76˚. CAD=33°, значит дуга DC равна 66°. Тогда дуга AD равна 10°. Стало быть, ABD=5°. Ответ: 5 .
Задача 5 . Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 13 и .
Решение : Радиус R описанной окружности около прямоугольника – половина диагонали. По т. Пифагора: AC= ; тогда R=9. Ответ: 9.
Задача 6 . Найдите сторону квадрата, вписанного в окружность радиуса
Решение : Диагональ BD квадрата – диаметр окружности. Обозначим сторону квадрата за x. Из треугольника ABD по т. Пифагора x 2 +x 2 =( ) 2 ; 2x 2 =90 2 ·2;
x 2 =90 2 ; x=90; Ответ: 90.
Задача 7 . Меньшая сторона прямоугольника равна 16. Угол между диагоналями равен 60˚. Найдите радиус описанной окружности этого прямоугольника.
Решение : Диагонали прямоугольника – диаметры окружности.
Треугольник ABO – равносторонний, так как O=60°, AO=BO=R. Значит, R=16. Ответ: 16.
Задача 8 . Около трапеции описана окружность. Периметр трапеции равен 60, средняя линия равна 25. Найдите боковую сторону трапеции.
Решение : Раз трапеция вписана в окружность, то она равнобедренная (AB=CD).
Средняя линия трапеции l есть полусумма оснований (BC+AD)/ 2, при этом l =25. P=2AB+(BC+AD); 60=2AB+50; AB=5; Ответ: 5.
Задача 9 . Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60˚, большее основание равно 82. Найдите радиус описанной окружности этой трапеции.
Решение : 1) Трапеция, вписанная в окружность, – равнобедренная.
HQ=BC=AB=CD, AH=QD (где H,D – основания высот, опущенных к большему основанию).Из прямоугольного треугольника ABH с углом B в 30˚ AH=0,5AB по свойству катета
против угла в 30˚. Значит, AD=2AH+HQ=AB+HQ=2AB; 2AB=82; AB=41.
2) Окружность описана и вокруг треугольника ABC.Треугольник равнобедренный с углом при вершине в 120˚. Значит, BAC= BCA=30°. Применяем теорему синусов: AB/sin30° =2R, где R – радиус окружности, описанной около треугольника ABC (и около трапеции ABCD). 41/=2R; R=41; Ответ: 41.
Задача 10 . Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Решение : Длина высоты трапеции HQ есть сумма длин высот OQ,OH треугольников OBC и OAD.
OQ= =4 (по т. Пифагора из треугольника OQC);
OH= = 3 (по т. Пифагора из треугольника OHD);
Задача 11 . Два угла вписанного в окружность четырехугольника равны 56˚ и 99˚. Найдите больший из оставшихся углов. Ответ дайте в градусах.
Решение : Данные два угла не могут быть противоположными, так как иначе их сумма должна была бы быть 180˚ (так как они опираются на дополняющие друг друга дуги до окружности).Если A=99°, то C=180°-99°=81°. Если B=56°, то D=180°-56°=124°. Угол D и есть наибольший. Ответ: 124.
Задача 12 .Найдите радиус окружности, описанной около прямоугольника ABCD, если стороны квадратных клеток равны 1.
Решение: Диаметр описанной окружности около прямоугольника – диагональ прямоугольника. R = BD: 2=2,5. Ответ: 2,5.
Задача 13 . Периметр правильного шестиугольника равен 108. Найдите диаметр описанной окружности.
Решение: AB=BC=. =EF= P: 6 = 108 : 6 =18. Рассмотрим треугольник AOF. Он равносторонний, т.к. AO=OF=R и AOF=60°. Значит, диаметр окружности D есть 2 ·18=36. Ответ: 36.
Задача 14. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 72˚. Найдите n.
Решение: Рассмотрим треугольник AОB. Он равнобедренный, так как AO=BO=R.
Значит, A= B и AOB=180°-2 · 72°=36°.Таких равных равнобедренных треугольников у нас n штук, в сумме углы при вершине O этих треугольников дают 360˚.Тогда n=360°/=10. Ответ: 10.
Задача 15 . Около окружности, радиус которой равен ,описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника.
Решение: Треугольники AOB,BOC и т.д. – равные, равносторонние. Их сторона равна радиусу описанной около правильного шестиугольника окружности.
Из прямоугольного треугольника AOP, (где OP=R, R – радиус окружности, вписанной в правильный шестиугольник): sinA=OP/AO; , АО=3 Ответ: 3
Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

По теме: методические разработки, презентации и конспекты
Рабочая программа по элективному курсу по геометрии «Решение планиметрических задач на вписанные и описанные окружности» 9 класс
Статистические данные анализа результатов проведения ЕГЭ говорят о том, что наименьший процент верных ответов традиционно дается учащимися на геометрические задачи. Задачи по планиметрии, включаемые в.
ЭЛЕКТИВНЫЙ КУРС «РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ НА ВПИСАННЫЕ И ОПИСАННЫЕ ОКРУЖНОСТИ» по геометрии для учащихся 9 классов
Древние греки считали окружность совершеннейшейи «самой круглой» фигурой, И в наше время в некоторыхситуациях, когда хотят дать особую оценку, используют слово «кругл.
Методическая разработка элективного курса «РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ НА ВПИСАННЫЕ И ОПИСАННЫЕ ОКРУЖНОСТИ» по геометрии для учащихся 9 класса
Статистические данные анализа результатов проведения ЕГЭ говорят о том, что наименьший процент верных ответов традиционно дается учащимися на геометрические задачи. Задачи по планиметрии, включаемые в.
Решение задач на вписанные и описанные многогранники
Решение задач на вписанные и описанные многогранники.
Презентация «Вписанные и описанные конусы». Решение задач
презентация по теме: «Решение задач на вписанные и описанные многогранники (пирамида)
Данная презентация позволяет организавать устную работу на уроке в 11 классе по готовым чертежам.
Презентация «Вписанная и описанная окружности четырехугольника» Геометрия 8 класс Мерзляк
Презентация «Решение задач на тему «Вписанная и описанная окружности четырехугольника» Геометрия 8 класс Мерзляк.
Видео:Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать

Задачи на вписанные четырехугольники в окружность
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Решение вписанные и описанные четырехугольники для ОГЭ и ЕГЭ
методическая разработка по геометрии (9 класс) на тему
Предложены решения задач из баннка данных для ОГЭ и ЕГЭ. Удобно использовать для коррекции знаний или для учащихся, пропустивших занятия по подготовке к итоговой атттестации
Видео:8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4Скачать

Скачать:
| Вложение | Размер |
|---|---|
| reshenie_vpis_i_opis_chetyrehugolniki_ege_i_oge_.doc | 386 КБ |
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Предварительный просмотр:
Окружность, вписанная в многоугольни к http://egemaximum.ru/zadachi-7-mnogougolnik-i-okruzhnost/
Задача 1 . Найдите радиус окружности, вписанной в квадрат со стороной 16.
Решение: Радиус вписанной окружности в квадрат – есть половина стороны квадрата. Поэтому r = 8
Задача 2 . Сторона ромба равна 58, острый угол равен 30˚. Найдите радиус вписанной окружности этого ромба.
Решение: Пусть точки касания окружности противоположных сторон ромба – E и T. Тогда ET– диаметр окружности (точка пересечения диагоналей О – центр симметрии параллелограмма, значит и ромба).
ET – есть расстояние между противоположными сторонами ромба так же, как и высота ромба (DH).
Рассмотрим прямоугольный треугольник ADH. Так как угол А равен 30°по условию, то катет HD, противолежащий этому углу, равен половине гипотенузы AD. То есть HD=ET=29. Значит, радиус вписанной окружности есть ET: 2, то есть 14,5. Ответ: 14,5.
Задача 3 . Найдите высоту трапеции, в которую вписана окружность радиуса 14.
Решение: Высота трапеции – есть диаметр вписанной окружности в трапецию.
h=2r=2·14, h = 28. Ответ:28
Задача 4. Боковые стороны трапеции, описанной около окружности, равны 19 и 13. Найдите среднюю линию трапеции.
Решение: в трапецию вписана окружность, значит BC+AD=AB+CD, что хорошо видно на картинке (равные отрезки помечены согласно свойству отрезков касательных).Итак, BC+AD=32, средняя линия l – есть полусумма оснований, то l =16.
Задача 5. Периметр прямоугольной трапеции, описанной около окружности, равен 80, ее большая боковая сторона равна 30. Найдите радиус окружности
Решение: в трапецию вписана окружность, значит BC+AD=AB+CD и P ABCD =80, то AB+CD= P:2 = 40. CD=30 по условию, то AB=10.
Далее, AB=NQ=2r. r =5. Ответ:5
Задача 6. В четырехугольник ABCD вписана окружность, AB=52, CD=53. Найдите периметр четырехугольника.
Решение: Раз в выпуклый четырехугольник ABCD вписана окружность, то AB+CD=BC+AD. P ABCD =2(AB+CD)=2(52+53)=210
Задача 7 . Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1:17:23 . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 84.
Решение: В выпуклый четырехугольник ABCD вписана окружность, значит AB+CD=BC+AD. По условию три стороны четырехугольника относятся как 1:17:23, пусть тогда AD=x;AB=17x; BC=23x. Итого, 24x=17x+CD; 7x=CD;
Наконец, так как по условию периметр четырехугольника равен 84, то 24x=42;
x= 7/4.Очевидно, большая сторона – это BC=23x. BC=23·(7/4) = 40,25.
Задача 8 . Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
Решение: Сторона квадрата вдвое больше радиуса вписанной в него окружности. Поэтому сторона квадрата равна . Радиус описанной вокруг квадрата окружности равен половине его диагонали. Поэтому радиус описанной окружности есть . Ответ: 6.
Задача 9 . Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен
Решение: Шестиугольник составлен из 6 правильных треугольников. Рассмотрим правильный треугольник AOF: В нем OH = r – медиана и высота, , , тогда , АО=66 Ответ: 66.
Окружность, описанная около многоугольни к http://egemaximum.ru/zadachi-7-mnogougolnik-i-okruzhnost/
Задача 1 . Угол A четырехугольника ABCD, вписанного в окружность, равен 26˚. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
Решение: Вписанный в окружность угол A опирается на дугу BCD, значит дуга BCD=52° по свойству вписанного угла. Дуга BAD, дополняющая дугу BCD до окружности, равна 360°-52°=308°. Тогда угол Cравен 308°: 2 = 154°. Ответ: 154.
Задача 2. Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 78˚, 107˚, 39˚, 136˚. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
Решение: Вписанный угол C опирается на дугу BAD, равную 78˚+136˚=214˚.
Значит сам угол равен 214 : 2 = 107˚. Ответ: 107.
Задача 3 . Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как 1:2:7:26. Найдите угол A четырехугольника ABCD. Ответ дайте в градусах.
Решение: Дуги AB,BC,CD,AD в сумме составляют 360˚. Так как градусные меры дуг AB, BC, CD и AD относятся соответственно как 1:2:7:26, то пусть AB=x, BC=2x, CD=7x,AD=26x градусов. Имеем, x+2x+7x+26x=360;36x=360;x=10. Угол A опирается на дугу BD=9x градусов, значит угол A равен 90˚: 2 = 45˚. Ответ: 45 .
Задача 4 . Четырехугольник ABCD вписан в окружность. Угол ABC равен 38˚, угол CAD равен 33˚. Найдите угол ABD. Ответ дайте в градусах.
Решение : ABC=38˚, значит дуга ADC равна 76˚. CAD=33°, значит дуга DC равна 66°. Тогда дуга AD равна 10°. Стало быть, ABD=5°. Ответ: 5 .
Задача 5 . Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 13 и .
Решение : Радиус R описанной окружности около прямоугольника – половина диагонали. По т. Пифагора: AC= ; тогда R=9. Ответ: 9.
Задача 6 . Найдите сторону квадрата, вписанного в окружность радиуса
Решение : Диагональ BD квадрата – диаметр окружности. Обозначим сторону квадрата за x. Из треугольника ABD по т. Пифагора x 2 +x 2 =( ) 2 ; 2x 2 =90 2 ·2;
x 2 =90 2 ; x=90; Ответ: 90.
Задача 7 . Меньшая сторона прямоугольника равна 16. Угол между диагоналями равен 60˚. Найдите радиус описанной окружности этого прямоугольника.
Решение : Диагонали прямоугольника – диаметры окружности.
Треугольник ABO – равносторонний, так как O=60°, AO=BO=R. Значит, R=16. Ответ: 16.
Задача 8 . Около трапеции описана окружность. Периметр трапеции равен 60, средняя линия равна 25. Найдите боковую сторону трапеции.
Решение : Раз трапеция вписана в окружность, то она равнобедренная (AB=CD).
Средняя линия трапеции l есть полусумма оснований (BC+AD)/ 2, при этом l =25. P=2AB+(BC+AD); 60=2AB+50; AB=5; Ответ: 5.
Задача 9 . Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60˚, большее основание равно 82. Найдите радиус описанной окружности этой трапеции.
Решение : 1) Трапеция, вписанная в окружность, – равнобедренная.
HQ=BC=AB=CD, AH=QD (где H,D – основания высот, опущенных к большему основанию).Из прямоугольного треугольника ABH с углом B в 30˚ AH=0,5AB по свойству катета
против угла в 30˚. Значит, AD=2AH+HQ=AB+HQ=2AB; 2AB=82; AB=41.
2) Окружность описана и вокруг треугольника ABC.Треугольник равнобедренный с углом при вершине в 120˚. Значит, BAC= BCA=30°. Применяем теорему синусов: AB/sin30° =2R, где R – радиус окружности, описанной около треугольника ABC (и около трапеции ABCD). 41/ =2R; R=41; Ответ: 41.
Задача 10 . Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Решение : Длина высоты трапеции HQ есть сумма длин высот OQ,OH треугольников OBC и OAD.
OQ= =4 (по т. Пифагора из треугольника OQC);
OH= = 3 (по т. Пифагора из треугольника OHD);
Задача 11 . Два угла вписанного в окружность четырехугольника равны 56˚ и 99˚. Найдите больший из оставшихся углов. Ответ дайте в градусах.
Решение : Данные два угла не могут быть противоположными, так как иначе их сумма должна была бы быть 180˚ (так как они опираются на дополняющие друг друга дуги до окружности).Если A=99°, то C=180°-99°=81°. Если B=56°, то D=180°-56°=124°. Угол D и есть наибольший. Ответ: 124.
Задача 12 .Найдите радиус окружности, описанной около прямоугольника ABCD, если стороны квадратных клеток равны 1.
Решение: Диаметр описанной окружности около прямоугольника – диагональ прямоугольника. R = BD: 2=2,5. Ответ: 2,5.
Задача 13 . Периметр правильного шестиугольника равен 108. Найдите диаметр описанной окружности.
Решение: AB=BC=. =EF= P: 6 = 108 : 6 =18. Рассмотрим треугольник AOF. Он равносторонний, т.к. AO=OF=R и AOF=60°. Значит, диаметр окружности D есть 2 ·18=36. Ответ: 36.
Задача 14. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 72˚. Найдите n.
Решение: Рассмотрим треугольник AОB. Он равнобедренный, так как AO=BO=R.
Значит, A= B и AOB=180°-2 · 72°=36°.Таких равных равнобедренных треугольников у нас n штук, в сумме углы при вершине O этих треугольников дают 360˚.Тогда n=360°/ =10. Ответ: 10.
Задача 15 . Около окружности, радиус которой равен ,описан правильный шестиугольник. Найдите радиус окружности, описанной около этого шестиугольника.
Решение: Треугольники AOB,BOC и т.д. – равные, равносторонние. Их сторона равна радиусу описанной около правильного шестиугольника окружности.
Из прямоугольного треугольника AOP, (где OP=R, R – радиус окружности, вписанной в правильный шестиугольник): sinA=OP/AO; , АО=3 Ответ: 3
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

По теме: методические разработки, презентации и конспекты
Рабочая программа по элективному курсу по геометрии «Решение планиметрических задач на вписанные и описанные окружности» 9 класс
Статистические данные анализа результатов проведения ЕГЭ говорят о том, что наименьший процент верных ответов традиционно дается учащимися на геометрические задачи. Задачи по планиметрии, включаемые в.
ЭЛЕКТИВНЫЙ КУРС «РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ НА ВПИСАННЫЕ И ОПИСАННЫЕ ОКРУЖНОСТИ» по геометрии для учащихся 9 классов
Древние греки считали окружность совершеннейшейи «самой круглой» фигурой, И в наше время в некоторыхситуациях, когда хотят дать особую оценку, используют слово «кругл.
Методическая разработка элективного курса «РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ НА ВПИСАННЫЕ И ОПИСАННЫЕ ОКРУЖНОСТИ» по геометрии для учащихся 9 класса
Статистические данные анализа результатов проведения ЕГЭ говорят о том, что наименьший процент верных ответов традиционно дается учащимися на геометрические задачи. Задачи по планиметрии, включаемые в.
Решение задач на вписанные и описанные многогранники
Решение задач на вписанные и описанные многогранники.
Презентация «Вписанные и описанные конусы». Решение задач
презентация по теме: «Решение задач на вписанные и описанные многогранники (пирамида)
Данная презентация позволяет организавать устную работу на уроке в 11 классе по готовым чертежам.
Презентация «Вписанная и описанная окружности четырехугольника» Геометрия 8 класс Мерзляк
Презентация «Решение задач на тему «Вписанная и описанная окружности четырехугольника» Геометрия 8 класс Мерзляк.
Видео:ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

Четырёхугольник вписан в окружность
Четырёхугольник вписан в окружность (задачи). Продолжаем рассматривать задания входящие в состав ЕГЭ по математике. В этой статье мы решим несколько задач с использованием свойств вписанного угла. Теория была подробно уже изложена, обязательно посмотрите . В указанной статье решение заданий по сути сводилось к применению свойства вписанного угла сразу же, то есть это были задания практически в одно действие. Здесь нужно чуть подумать, ход решения не всегда с ходу очевиден.
Применяются: теорема о сумме углов треугольника, свойства вписанного угла, свойство четырёхугольника вписанного в окружность. О последнем подробнее.
*Это свойство было уже представлено, но в другой интерпретации. Итак:
Вписанный четырехугольник — это четырехугольник, все вершины которого лежат на одной окружности.
Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равны 180 градусам.
То есть, если мы такой четырёхугольник, то сумма его противоположных углов равна 180 градусам.
27870. В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 110 0 . Найдите вписанный угол ACB. Ответ дайте в градусах.
Треугольник BОC равнобедренный, так как ОС=ОВ (это радиусы). Известно, что сумма углов треугольника равна 180 градусам. Рассмотрим ∠BOC и ∠AOD:
Углы при основании равнобедренного треугольника равны, то есть
Угол АОВ является центральным углом для вписанного угла АСВ. По свойству вписанного в окружность угла
Сумма смежных углов равна 180 0 , значит
27871. Угол А четырехугольника ABCD, вписанного в окружность, равен 58 0 . Найдите угол C этого четырехугольника. Ответ дайте в градусах.
Здесь достаточно вспомнить свойство такого четырёхугольника. Известно, что сумма его противоположных углов такого равна 180 градусам, значит угол С будет равен
Построим ОВ и OD.
По свойству вписанного угла градусная величина дуги BCD равна
Следовательно градусная величина дуги BAD будет равна
360 0 – 116 0 = 244 0
По свойству вписанного угла угол С будет в два раза меньше, то есть 122 0 .
27872. Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95 0 , 49 0 , 71 0 , 145 0 . Найдите угол B этого четырехугольника. Ответ дайте в градусах.
Построим радиусы АО, OD, OC:
Градусная величина дуги AD равна 145 0 , градусная величина дуги СD равна 71 0 , значит градусная величина дуги АDС равна 145 0 + 71 0 = 216 0 .
По свойству вписанного угла угол В будет в два раза меньше центрального угла соответствующего дуге АDС, то есть
27874. Четырехугольник ABCD вписан в окружность. Угол ABC равен 105 0 , угол CAD равен 35 0 . Найдите угол ABD. Ответ дайте в градусах.
Данная задача может вызвать затруднение. Сразу невозможно явно увидеть ход решения. Вспомним, что известно про вписанный четырёхугольник: сумма его противоположных углов равна 180 градусам. Найдём
На данный момент мы нашли тот угол, который сразу же возможно определить по известному свойству. Если есть возможность найти какую-либо величину, сделайте это, пригодится. Действуем по принципу «находим то, что можно найти исходя из данных величин».
Далее используя теорему о сумме углов треугольника найдём угол ACD:
Вписанные углы ABD и ACD опираются на одну и туже дугу, это означает, что они равны, то есть
27875. Четырехугольник ABCD вписан в окружность. Угол ABD равен 75 0 , угол CAD равен 35 0 . Найдите угол ABC. Ответ дайте в градусах.
Известно, что вписанные углы опирающиеся на одну и ту же дугу, и лежащие от неё по одну сторону равны. Следовательно
В треугольнике ACD известно два угла, можем найти третий:
Далее воспользуемся свойством – известно, что у вписанного в окружность четырехугольника сумма противолежащих углов равна 180 0 , значит
27869. AC и BD — диаметры окружности с центром O. Угол ACB равен 38 0 . Найдите угол AOD. Ответ дайте в градусах.
27873. Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как 4:2:3:6. Найдите угол A четырехугольника ABCD. Ответ дайте в градусах.
27876. Четырехугольник ABCD вписан в окружность. Угол ABC равен 110 0 , угол ABD равен 70 0 . Найдите угол CAD. Ответ дайте в градусах.
Отмечу, что важно помнить указанные свойства и задачи вы решите без проблем. Конечно, можно выстроить решение не совсем корректно. Например, в задаче 27876 для самостоятельного решения приведено «длинное», или как ещё говорят нерациональное решение. Ничего страшного, если вы именно также решите задачу.
Главное чтобы вы помнили и применяли теорию, и в конечном итоге РЕШИЛИ задание.
В данной рубрике продолжим рассматривать задачи, приглашаю вас на блог!
На этом всё. Успеха вам!
С уважением, Александр Крутицких
Комиссия спрашивает у директора простой сельской школы:
— По какой причине у вас все дети говорят: пришедши, ушедши?
— А кто их знает, может они так привыкши!
Видео:Все об окружностях на ЕГЭ | Профильная математика 2023 | УмскулСкачать

Дидактический материал по теме «Вписанные в окружность четырехугольники. Описанные около окружности четырехугольники.»
Дидактический материал по теме «Вписанные в окружность четырехугольники. Описанные около окружности четырехугольники.» Данные задачи можно использовать как на закрепление, так и на проверку знаний по теме.
Просмотр содержимого документа
«Дидактический материал по теме «Вписанные в окружность четырехугольники. Описанные около окружности четырехугольники.»»
Дидактический материал по теме «Вписанные в окружность четырехугольники. Описанные около окружности четырехугольники.»
Задача 1. Найдите все углы вписанного в окружность четырехугольника АВСD, если ∠ А=40º, а ∠D =90º
Задача 2. Противоположные стороны четырехугольника, описанного около окружности, равны 7 см и 10 см. Можно ли по этим данным найти периметр четырехугольника?
Задача 3. Сумма сторон AB+CD=18 м. Найти периметр четырехугольника.
Задача 4. Три последовательные стороны четырехугольника, в который можно вписать окружность, равны 6 см, 8 см и 9 см. Найдите четвертую сторону и периметр этого четырехугольника.
Задача 5. Боковые стороны трапеции, описанной около окружности, равны 2 см и 4 см. Найдите среднюю линию трапеции.
Задача 6. Известно, что в трапецию ABCD с основаниями AD и ВС можно вписать окружность и около неё можно описать окружность, EF – её средняя линия. Известно, что АВ + CD + EF = 18. Найдите периметр трапеции (1)
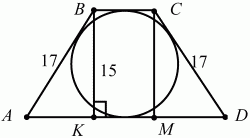
Задача 7. Около окружности с диаметром 15 см описана равнобедренная трапеция с боковой стороной, равной 17 см. Найдите основания трапеции (2)
1. В четырехугольник ABCD вписана окружность, AB = 10, BC = 11 и CD = 15. Найдите четвертую сторону четырехугольника.
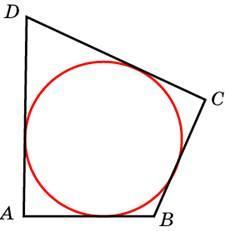
2. Два угла вписанного в окружность четырехугольника равны 84° и 57°. Найдите меньший из оставшихся углов. Ответ дайте в градусах.
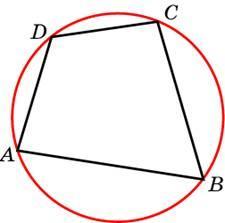
3. В четырехугольник ABCD вписана окружность, AB = 10, CD = 16. Найдите периметр четырехугольника.
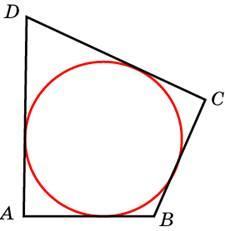
4. Четырехугольник ABCD вписан в окружность. Угол ABD равен 75°, угол CAD равен 35°. Найдите угол ABC. Ответ дайте в градусах.
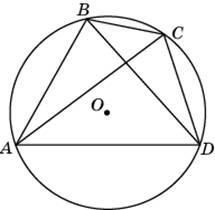
5. Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
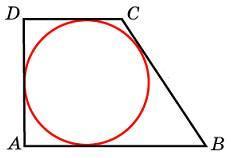
1. В четырехугольник ABCD вписана окружность, AB = 8, BC = 9 и CD = 14. Найдите четвертую сторону четырехугольника.

2. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

3. В четырехугольник ABCD вписана окружность, AD = 15, BC = 11. Найдите периметр четырехугольника.

4. Четырехугольник ABCD вписан в окружность. Угол ABC равен 105°, угол CAD равен 35°. Найдите угол ABD. Ответ дайте в градусах.
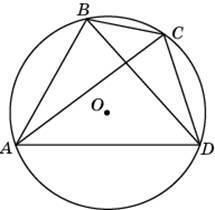
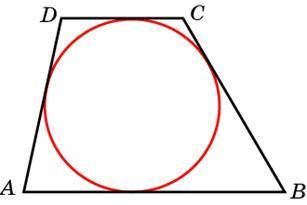
5. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
💡 Видео
16 задача ОГЭ: четырёхугольник, вписанный в окружность; подобные треугольникиСкачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

#58. Олимпиадная задача о четырехугольникеСкачать

Вписанные четырехугольники. 9 класс.Скачать

Вписанный в окружность четырёхугольник.Скачать

Геометрия 8 класс : Решение задач. Вписанная окружностьСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вписанная и описанная окружности. ЗадачиСкачать

Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать