Наибольшая площадь треугольника через производную

В геометрии существует множество задач, в которых требуется найти наибольшее или наименьшее значение функции. В качестве функции могут рассматриваться периметр или площадь фигуры или, например, объем тела, а аргументом функции служит какой-либо параметр фигуры или тела − длина стороны, угол между сторонами и т.п. После того, как функция составлена, ее необходимо исследовать с помощью производной на экстремальное значение. При этом следует учитывать, что обычно в таких примерах функция существует на конечном промежутке, который определяется геометрией системы и условием задачи.

Источник информации

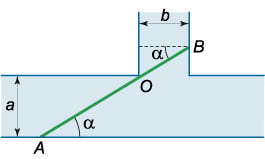
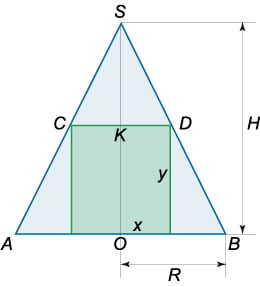
Рассмотрим треугольники (OBC) и (MBA.) Эти треугольники подобны. Следовательно, справедливо соотношение

где координаты (x) и (y) удовлетворяют соотношениям (x > a,) (y > b.) Отсюда выразим (y) через (x:)

Площадь треугольника будет описываться следующей функцией (Sleft( x right):)

Функция (Sleft( x right)) имеет критические точки (x = 0,) (x = a,) (x = 2.) Поскольку (x > a,) то решением является точка (x = 2a.) При переходе через нее производная меняет знак с минуса на плюс, т.е. (x = 2a) − точка минимума функции (Sleft( x right).)

Вычислим другой катет треугольника:

Таким образом, треугольник с наименьшей площадью имеет катеты, равные (2a) и (2b.)

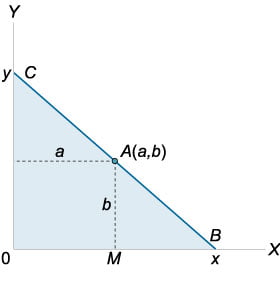
Равнобедренная трапеция описана вокруг окружности радиуса (R) (рисунок (2)). При каком угле при основании (alpha) площадь заштрихованной области будет наименьшей?

Площадь равнобедренной трапеции определяется формулой

где (a, b) − основания трапеции, (h) − ее высота. Очевидно, что (h = 2R.) Площадь круга равна ( = pi .) Тогда площадь заштрихованной области составляет

Поскольку трапеция описана вокруг окружности, то сумма противоположных сторон у нее одинакова, т.е.

Здесь через (ell) обозначена боковая сторона трапеции. Подставляя (left( right)) в предыдущее соотношение, получаем:

Исследуем площадь (Sleft( alpha right)) на экстремальное значение. Вычислим производную (S’left( alpha right):)

Видно, что производная равна нулю при условии

[cos alpha = 0,;; Rightarrow alpha = dfrac,]

причем при переходе через эту точку (при возрастании (alpha)) производная меняет знак с минуса на плюс. Следовательно, (alpha = largedfracnormalsize) − точка минимума функции (Sleft( alpha right).) В этом случае трапеция «вырождается» в квадрат. Минимальное значение площади фигуры определяется формулой

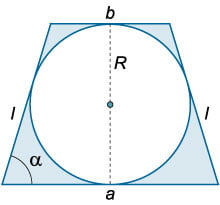
Окно имеет форму прямоугольника, ограниченного сверху полукругом (рисунок (3)). Периметр окна равен (P.) Определить радиус полукруга (R,) при котором площадь окна является наибольшей.

Очевидно, что одна сторона прямоугольника равна (2R.) Другую сторону обозначим через (y.) Периметр всего окна выражается формулой

[P = pi R + 2R + 2y.]

Отсюда находим (y:)

Площадь окна составляет:

Полученное выражение представляет собой функцию (Sleft( R right).) Исследуем ее на экстремум. Находим производную:

Определяем стационарные точки:

Поскольку вторая производная отрицательна:

[ <S''left( R right) = <left[ <P — left( right)R> right]^prime > > = < — left( right) Уровень 8 класс Предмет Математика Сложность Простая

В область, ограниченную параболой (y = c — ) и осью (Ox,) вписан прямоугольник, стороны которого параллельны координатным осям и одна сторона лежит на оси (Ox.) Определить наибольшую площадь прямоугольника.

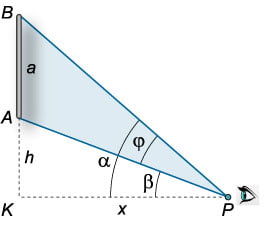
Таким образом, оптимальное расстояние от стены для наилучшего обзора картины определяется формулой [x = sqrt <hleft( right)> .] Например, если (a = 3,text) и (h = 2,text,) то оптимальное расстояние составляет [ <x = sqrt <hleft( right)> = sqrt <2left( right)> > = <sqrt approx 3,16,text.> ]

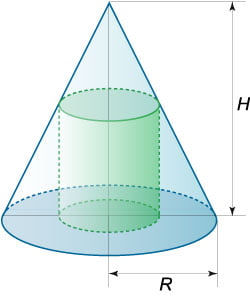
Рис.9 Оптимальная форма цилиндра при заданном объеме позволяет уменьшить расходы на материалы. Поэтому такая задача актуальна, например, при строительстве нефтехранилищ (рисунок (9)).

Пусть (H) − высота цилиндра, а (R) − радиус его основания. Объем и полная площадь поверхности цилиндра вычисляются по формулам [V = pi H,;;;S = 2pi + 2pi RH.] В качестве независимой переменной выберем радиус основания (R.) Выразим (H) через (R) (при заданном объеме (V) ): [H = frac<<pi >>.] Исследуем площадь поверхности (Sleft( R right)) на экстремум. [ <Sleft( R right) = 2pi + 2pi RH > = <2pi + 2pi R cdot frac<<pi >> > = <2pi + frac<>.> ] Вычисляем производную: [ <S'left( R right) = <left( <2pi + frac<>> right)^prime > > = <4pi R — frac<><<>> > = <frac<<4pi — 2V>><<>>.> ] Находим стационарные точки: [ ;; <Rightarrow frac<<4pi — 2V>><<>> = 0,>;; <Rightarrow left< <begin<*> <4pi — 2V = 0>\ <ne 0> end,> right.>;; <Rightarrow R = sqrt[large 3normalsize]<<frac<>>>.> ] Данное значение (R) соответствует минимальной площади поверхности (Sleft( R right),) поскольку при переходе через эту точку производная меняет знак с минуса на плюс.

Рис.11 Рассмотрим осевое сечение вписанного в шар конуса (рисунок (11)). Введем следующие обозначения: (H) − высота конуса, (r) − радиус основания конуса, (alpha) − угол между радиусом и основанием конуса. Радиус основания и высота конуса связаны с радиусом шара следующими соотношениями: [r = Rcos alpha ,;;;H = Rsin alpha + R.] В таком случае объем конуса можно представить в виде [ <V = fracpi H > = <fracpi <left( right)^2>left( right) > = <fracpi alpha left( right).> ] где угол (alpha) изменяется в интервале (0 Уровень 8 класс Предмет Математика Сложность Простая

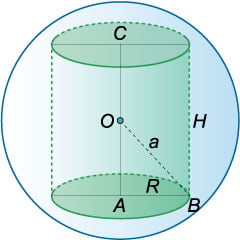
Рис.13 Объем цилиндра равен [V = pi H.] Радиус основания цилиндра (R) связан с радиусом шара (a) следующим соотношением (рисунок (13)): [ <= + <left( <frac> right)^2> > = <+ frac<<>>.> ] Следовательно, [ = — frac<<>>.] Подставляя это в формулу для объема цилиндра, получаем: [ <V = pi H = pi left( <— frac<<>>> right)H > = <pi H — frac<<pi >>.> ] Данное выражение представляет собой функцию (Vleft( H right),) которое мы будем исследовать далее на экстремум. Производная (V’left( H right)) имеет вид: [ <V'left( H right) = <left( <pi H — frac<<pi >>> right)^prime > > = <pi — frac<<3pi >> > = <fracleft( <4— 3> right).> ] Корни производной равны: [ ;; <Rightarrow 4— 3 = 0,>;; <Rightarrow = frac<<4>>,>;; <Rightarrow H = pm frac<><>.> ] Разумеется, нас устраивает лишь положительное значение (H = largefrac<><>normalsize.) При переходе через эту точку производная меняет знак с плюса на минус, т.е. здесь существует максимум функции (Vleft( H right).) При такой высоте (H) радиус основания цилиндра равен [ <= — frac<<>> > = <— frac<left( <frac<><>> right)^2> > = <— frac<<4>><> > = <— frac<<>> > = <frac<<2>>,>;; <Rightarrow R = asqrt <frac> .> ] Итак, вписанный в шар цилиндр имеет наибольший объем при условии [H = frac<><>,;;;R = asqrt <frac> ,] где (a) − радиус шара. Максимальное значение объема составляет [ <V = pi H > = <pi <left( <asqrt <frac> > right)^2> cdot frac<><> > = <frac<<2pi >> cdot frac<><> > = <frac<<4pi >><>,> ] т.е. меньше объема шара в (sqrt 3) раз.

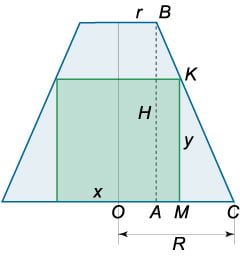
Рис.14 Будем считать, что оси бревна и балки совпадают. Усеченный конус и вписанный в него параллелепипед схематически показаны в разрезе на рисунке (14.) Объем параллелепипеда определяется формулой [V = y,] где (x) − сторона квадрата в основании параллелепипеда, а (y) − его высота.

Видео:10. ФНП. Градиент и производная по направлению функции двух переменных.Скачать

Задачи на экстремумы. Оптимизации

Содержание:

Видео:Математика это не ИсламСкачать

Задачи на экстремумы. Оптимизации

В реальной жизненной ситуации возникает необходимость выбора оптимального варианта и нахождения экстремумов определенной функции. Ежедневно, при решении проблем в различных областях, мы сталкиваемся с терминами наибольшая прибыль, наименьшие затраты, наибольшее напряжение, наибольший объем, наибольшая площадь и т.д. Большое экономическое значение в промышленности, при определении дизайна упаковки, имеет вопрос, как подобрать размеры упаковки с наименьшими затратами. Такого рода задания связаны с нахождением максимального или минимального значения величины. Задачи на нахождение максимального и минимального значения величины называются задачами на оптимизацию. Для решения данных задач применяется производная.

Замечание 1: На интервале должны учитываться предельные значения функции на концах.

Замечание 2: В рассматриваемом интервале может быть одна стационарная точка: или точка максимума, или точка минимума. В этом случае, в точке максимума функция принимает наибольшее значение, а в точке минимума — наименьшее значение.

Пример задачи на максимальный объем

Фирма планирует выпуск коробки без крышки, с квадратным основанием и площадью поверхности 192 см². Найдите размеры коробки, при которых она будет иметь наибольший объем?

Решение:

Так как основанием коробки является квадрат, то ее объем можно вычислить по формуле . Используя другие данные задачи, выразим объем только через одну переменную . Вычислим площадь поверхности коробки. Она равна 192 см² и состоит из 4 площадей боковых граней + площадь основания.

. Тогда выразим и подставим в формулу . Зависимость объема коробки от переменной можно выразить следующим образом:

Теперь найдем область определения функции , согласно условию задачи.

Понятно, что длина не может быть отрицательной, т.е. . Площадь квадрата в основании коробки должна быть меньше 192, т.е.

или Значит,

Найдем максимальное значение функции на интервале Для этого используем производную первого порядка:

При и имеем, что .

Однако, . Значит, в рассматриваемом интервале критической точкой является .

При имеем , при имеем , функция в точке принимает максимальное значение.

Если длина основания коробки будет 8 см, то высота будет равна , 192 — 82

Значит, максимальный объем будет иметь коробка с размерами 8см х 8см х 4см.

Построив при помощи графкалькулягора график функции , также можно увидеть, что при объем имеет максимальное значение. Постройте график функции при помощи производной и убедитесь в правильности решения.

Пример задачи на минимальное потребление

Два столба высотой 4 м и 12 м находятся на расстоянии 12 м друг от друга. Самые высокие точки столбов соединены с металлической проволокой, каждая из которых, в свою очередь крепится на земле в одной точке. Выберите такую точку на земле, чтобы для крепления использовалось наименьшее количество проволоки.

Решение:

1) Изобразим рисунок, соответствующий условию задачи, и обозначим соответствующие данные на рисунке.

2) Аналитически выразим зависимость между переменными.

• Длину проволоки обозначим через . Часть проволоки от каждого столба обозначим соответственно через и , тогда .

• Величина изменяется в зависимости от точки крепления на земле. Обозначим одно из них через , тогда другое будет равно 12-. Выразим величины и через переменную .

По теореме Пифагора:

зависимость функции от переменной будет

.

Производная функции :

Найдем критические точки функции :

Сравнивая значения функции в точках , , (это проверьте самостоятельно), получим, что наименьшее количество проволоки используется при (метр)

При решении задач на экстремумы обратите внимание на следующее!

1. Внимательно читайте условие. Сделайте соответствующий рисунок.

2. Задайте список соответствующих переменных и констант, которые менялись и оставались неизменными и какие единицы использовались. Если на рисунке есть размеры, обозначьте их.

3. Выберите соответствующий параметр и выразите искомую величину функцией . Найдите экстремумы данной функции.

4. Полученные значения объясните экспериментально.

Пример задачи на минимальное потребление материала.

Для мясных консервов планируется использовать банку в форме цилиндра объемом 250 см³.

a) Каких размеров должна быть банка, чтобы для ее изготовления использовалось как можно меньше материала?

b) Для круглого основания используется материал, цена 1 см² которого равна 0,05 гяпик, а для боковой поверхности используется материал цена 1 см² которого равна 0,12 гяпик. Какие размеры должна иметь банка, чтобы затраты на ее изготовление были минимальными?

Решение:

а) По условию задачи объем равен 250 см³. Эти данные дают нам возможность найти зависимость между и .

Для функции, выражающей площадь поверхности, область определения представляет собой незамкнутый интервал, и мы должны найти, при каком значении , где , функция имеет наименьшее значение. Найдем производную функции .

Критическая точка функции: При имеем , при .

Значит,

Подставим значение в формулу для высоты , получим .

Итак, минимальные затраты на материал будет иметь банка цилиндрической формы с размерами см и см.

b)

Размеры, при которых затраты на материал будут минимальными см, см.

Должны ли совпадать результаты, полученные в пунктах а) и b)? Проведите обсуждение.

Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:

Другие темы которые вам помогут понять математику:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Решение прикладных задач с помощью производной функции

Разделы: Математика

«Что значит владение математикой? Это есть умение решать задачи.
Причем не только стандартные, но и требующие известной независимости
мышления, здравого смысла, оригинальности, изобретательности».
Д. Пойа

Цели урока:

• Дидактические: рассмотреть применение метода поиска наибольших и наименьших значений функции к решению разнообразных прикладных задач, в первую очередь, задач на оптимизацию.
• Развивающие цели: развивать гибкость мышления, творческое отношение к изучаемому предмету, формировать независимость математического мышления в ходе решения задач.
• Воспитательные цели: на примере решения прикладных задач с простейшими жизненными ситуациями показать применение методов математического моделирования, поддержать этим интерес к предмету.

Вид занятия. Применение знаний, умений и навыков.

Оборудование. Интерактивная доска, карточки.

Методы – объяснительно-иллюстративное изложение, иллюстративный и демонстрационный.

План урока.

1. Нахождение наибольшего и наименьшего значений функции на промежутке.
2. Решение задач на нахождение наибольшего и наименьшего значений

Введение.

Современные требования к уроку предполагают использование новых подходов в преподавании математики. При подготовке к уроку преподаватель все чаще использует компьютерные технологии. Уроки с использованием презентаций становятся более насыщенными, эффективными и дают возможность развивать у студентов интерес к предмету, познавательную активность, творческий подход.

На данном уроке применение интерактивной доски должно наряду с самой темой привлечь внимание студентов к прикладной направленности математики. Одновременно текстовые задачи рассматриваются не только как прикладные, но и как умственные манипуляторы. Существует важное сходство между математикой и детской игрой: в обоих случаях исключительно важно творческое воображение. Потребность в умственных манипуляциях никогда не кончается, она присуща и профессиональным математикам на самом высоком уровне.

Решение любой задачи, особенно сложной, требует от ребят напряженного труда и упорства. А упорство проявляется, если задача интересна. Значит, нужно преподавателю подбирать такие задачи, которые студенты хотели бы решать. Чаще всего интерес вызывают задачи практического содержания.

Еще один метод применен на данном уроке для мотивации решения прикладных задач: в их тексты включаются фамилии студентов той группы, где идет занятие. Они становятся прорабами, предпринимателями, хозяевами предприятий и т.д.

Ход урока

1. Организационное начало

Приветствие студентов. Проверка присутствующих.

Сообщение темы занятия и плана работы, конкретизация задач и создание мотивации учебной деятельности. Прием – повествовательное изложение, форма – рассказ-вступление, Для быстрого включения студентов в работу на экран можно вывести слайд, содержащий информацию о плане урока, его целях и задачах.

2. Повторение опорных знаний студентов.

Провести дидактическую игру «Крестики- нолики» по теме «Производная функции». К доске приглашаются два студента. На доске подготовлено игровое поле. Первый, ответивший на вопрос преподавателя по данной теме, получает право выбрать знак («крестик» или «нолик») для себя и назвать первое окошко игрового поля. Если он решает правильно выпавшее ему задание, то имеет право поставить в данное окошко свой знак. Если ему это не удается, то право решить его отдается второму игроку. В итоге побеждает тот, кто закрывает своими значками 3 клетки по диагонали, горизонтали, вертикали или больше, чем 4 клетки.

Задания.

1. =
2. = ,
3. = ,
4. = ln cosx,
5. = ,
6. = x+ ,
7. = x,
8. = ,
9. = 2.

3. Применение знаний при решении примеров и задач.

Сегодня на занятии мы вспомним задания на нахождение наибольшего, наименьшего значений функции на промежутке и применение этой темы для решения задач. На прошлом занятии мы записали алгоритм для этого. Повторим его (приглашается для ответа студент, а затем еще раз выводится на экран).

Нахождение наибольшего и наименьшего значений монотонной функции f(x) на отрезке (а;в) достигается на концах отрезка. Если же заданная функция не является монотонной, но известно, что она является непрерывной, то для нахождения наибольшего и наименьшего значений функции на отрезке применяется правило:

1. Найти критические точки функции.
2. Найти значения функции в критических точках, принадлежащих отрезку, и на концах отрезка. Наибольшее и наименьшее значения из этих чисел и будут соответственно наибольшим и наименьшим значениями функции на отрезке.

Теперь решаем задачи.

Задача 1. Молодой предприниматель Михайлов Юрий в свете экономического кризиса решил выкупить нерентабельное провинциальное перерабатывающее предприятие и пригласил экономиста Гульдерова Германа помочь с расчетами по оптимизации расходов. Одна из задач поставленных перед Германом была следующая: найти, при каких условиях расход жести на изготовление консервных банок цилиндрической формы заданной емкости будет наименьшим.

Вспомним 3 этапа математического моделирования, применяемые при решении задач на оптимизацию (показ на экране):

• 1 этап. Составление математической модели.
• 2 этап. Работа с составленной моделью.
• 3 этап. Ответ на вопрос задачи.

1 этап. Составление математической модели.

Составление модели облегчается тем, что известна форма банки и оговорено, что она должна быть заданной емкости. Это существенно для составления модели. Существенным является также требование, чтобы расход жести на изготовление банки был минимальным. Это требование означает, что площадь полной поверхности банки, имеющей форму цилиндра, должна быть наименьшей; существенны и размеры банки. Несущественны для составления математической модели конкретное (численное) значение емкости банки и вид консервов (мясных, овощных), для которых банка предназначена.

Обозначив емкость банки через V см³, сформулируем задачу: Определить размеры цилиндра с объемом V см³ так, что бы площадь его полной поверхности была наименьшей.

Для решения задачи обозначим радиус основания цилиндра через х, а высоту его через h (все измерения в сантиметрах). Тогда объем цилиндра

V = h = .

Полная поверхность цилиндра:

S = 2x² + 2x h = 2x² + 2x = 2x² + = .

Итак, S(х) = .

Так как переменная х может принимать только положительные значения, решение задачи сводится к нахождению наименьшего значения S(х) на (0;).

2 этап. Работа с составленной моделью.

Найдем производную S´(х):

S´(х) = = .

Для нахождения критических точек решим уравнение S´(х) = 0.

Корень уравнения: х = .

При х S´(х) > 0.

Следовательно, в точке х = S(х) имеет минимум.

Следовательно, функция в этой точке достигает наименьшего значения.

Таким образом, площадь полной поверхности цилиндра, имеющего объем V, будет наименьшей при h = 2x = 2 = , т.е. когда цилиндр равносторонний.

3 этап. Ответ на вопрос задачи.

Наименьший расход жести на изготовление консервных банок цилиндрической формы заданной емкости будет достигнут при условии, что диаметр основания и высота банки равны между собой.

Полезно обратить внимание ребят на то, что в нашей стране выпускаются ежегодно сотни миллионов банок консервов в жестяной упаковке. Экономия 1% жести на изготовление каждой банки позволит за счет сэкономленного материала дополнительно изготовить несколько миллионов новых банок. Вместе с тем промышленность нередко выпускает консервы в жестяной таре, не обеспечивая наименьший расход материала на изготовление банки. Это обусловлено рядом причин: стремлением минимизации отходов при изготовлении банок, соображениями торговой эстетики. Возможностями транспортировки и т.д.

Задача 2. Фрагмент рассказа Л.Н. Толстого «Много ли человеку земли нужно» о крестьянине Пахоме, покупавшем землю у башкир.

— А цена какая будет? – говорит Пахом.

— Цена у нас одна: 1000 рублей за день.

— Какая же это мера – день? Сколько в ней десятин будет?

— Мы этого, – говорит, — не умеем считать. А мы за день продаем; сколько обойдешь за день , то твое, а цена 1000 рублей.

— Да ведь это, — говорит, — в день обойти земли много будет.

— Вся твоя, — говорит. – Только один уговор: если назад не придешь в день к тому месту, с какого возьмешься, пропали твои деньги.

Фигура, которая получилась у Пахома, изображена на рисунке( на экране).

Обежал он за день, например, прямоугольную трапецию периметром 40 км. С площадью S = 78 км².

Проверим, наибольшую ли площадь при этом получил бы Пахом (с учетом того, что участки обычно имеют форму прямоугольника)?

Р = 40 км. a – первая сторона, 20 – а – вторая сторона.

🎥 Видео

Наибольшее и наим. значения функции на отрезкеСкачать

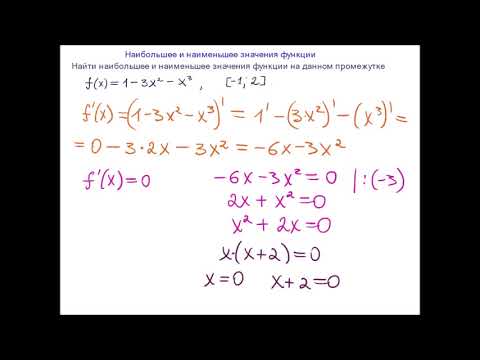
Наибольшее и наим. зн. функции Ч. 2Скачать

Задача из КембриджаСкачать

Наибольшее и наименьшее зн. функции Ч. 3Скачать

Страшная площадь треугольникаСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Как доказать, что площадь треугольника будет постоянной ?Скачать

Производные с нуля до уровня ЕГЭ №8Скачать

ЗАДАНИЕ №7 Производная и графики функции | PARTAСкачать

10 класс, 44 урок, Применение производной для исследования функций на монотонность и экстремумыСкачать

11 задание ЕГЭ математика. Производная с нуляСкачать

Приложение производной. Применение производной при решении задач. Урок №60Скачать

Щелчок по математике I №7,11 Производная. Вся теория и решение прототипов ФИПИСкачать

#49. ЗАЧЕМ НУЖНА ПРОИЗВОДНАЯ?Скачать

НАСКОЛЬКО ТЫ ОБРАЗОВАН? Тест на эрудицию из 30 вопросов. Империя ТестовСкачать

ЗАЧЕМ НУЖНЫ ЭТИ... производные! Математика на QWERTY.Скачать

Задача на параболу и площадь треугольникаСкачать