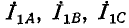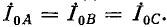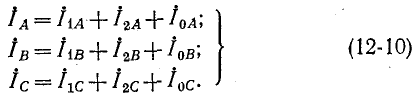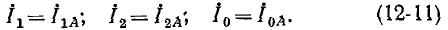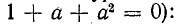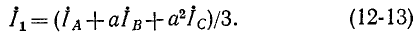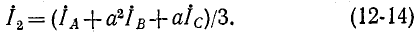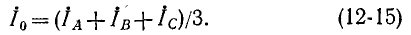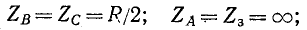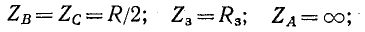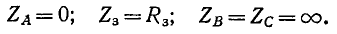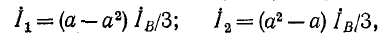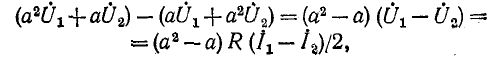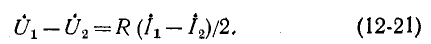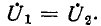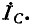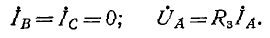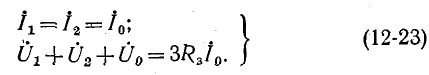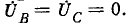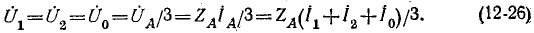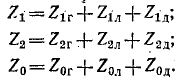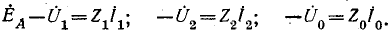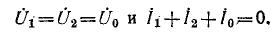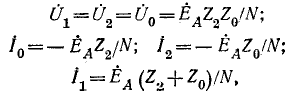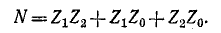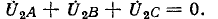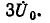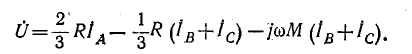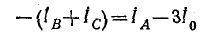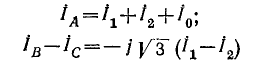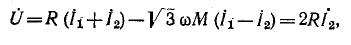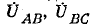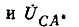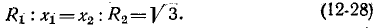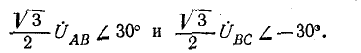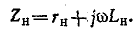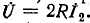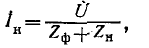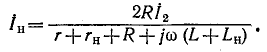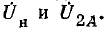Метод симметричных составляющих применяется для расчета трехфазных цепей в несимметричных режимах. Несимметричные режимы в энергосистеме возникают при различных видах коротких замыканий. Расчет токов коротких замыканий – важная инженерная задача в электроэнергетике, которая решается методом симметричных составляющих.
Математически любая несимметричная трехфазная система векторных величин (напряжений, токов и др.) может быть представлена в виде суммы (заменена суммой) из трех симметричных трехфазных систем, а именно: а) системы прямой последовательности с прямым порядком следования фаз A→B→C→A; б) системы обратной последовательности с обратным порядком следования фаз A→C→B→A; в) системы нулевой последовательности, ко¬торая состоит из трех равных векторов, совпадающих по фазе. Отдельные симмет-ричные системы векторов, на которые раскладывается несимметричная сис-тема, называются сим¬метричными составляющими. Вектора симметричных составляющих индексируются цифрами: 1 — для прямой последовательности, 2 — для обратной последовательности и 0 – для нулевой последовательности.
На рис. 42.1 представлены симметричные составляющие некоторой несимметричной трехфазной системы напряжений UA,UB,UC.
В методе симметричных составляющих для упрощения формы записи уравнений пользуются коэффициентом a=ej120° (поворотный множитель), умножением на который поворачивают вектор на угол в 120° без изменения его модуля. Свойства поворотного множителя: a2=ej240°=e-j120°, a3=1, a4=a, 1+a+a2=0.
Вектора исходной несимметричной системы определяются по принципу наложения как геометрические суммы соответствующих векторов симметричных составляющих:
Геометрическое сложение векторов симметричных составляющих согласно этим уравнениям показано на рис. 42.2.
Используя поворотный множитель “a” и “a2”, выразим все слагаемые правой части уравнений через симметричные составляющие фазы А:
Умножим все члены уравнения (2) на “a”, а все члены уравнения (3) на “a2”, сложим все три уравнения почленно и получим:
Из полученного уравнения следует формула для выделения симметричной составляющей прямой последовательности из несимметричной системы векторов:
Умножим все члены уравнения (2) на “a2”, а все члены уравнения (3) на “a”, сложим все три уравнения почленно и получим:
Из полученного уравнения следует формула для выделения симметричной составляющей обратной последовательности из несимметричной системы векторов:
Сложим все три уравнения (1), (2) и (3) почленно и получим:
Из полученного уравнения следует формула для выделения симметричной составляющей нулевой последовательности из несимметричной системы вектор:
Полученные формулы применяются на практике для разложения несимметричных трехфазных систем векторов на симметричные составляющие.
Видео:Разложение вектора по базису. 9 класс.Скачать
МЕТОД СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ
Сущность метода заключается в представлении несимметричной системы величин А, В, С в виде суммы трёх симметричных систем: прямой А1, В1, С1, имеющей такую же последовательность, как и исходные величины, обратной А2, В2, С2, имеющей противоположную последовательность, и нулевой последовательности, состоящей из трёх одинаковых по величине и направлению векторов А0.
Определение симметричных составляющих производится по формулам:
А0= 
(А + В + С), А1= (А + a×В + a 2 ×С), А2= (А + a 2 ×В + a×С),
где a = e j 120 ° – фазный множитель.
Сопротивления приёмника токам различных последовательностей называются сопротивлением прямой последовательности Z1, обратной последовательности Z2 и нулевой последовательности Z0. Для схемы Y–Y они имеют значения
где Z – сопротивление фазы приёмника, ZN – сопротивление нейтрали.
Для асинхронного двигателя характерно такое соотношение:
Расчёт симметричных цепей с несимметричным источником состоит из трёх этапов: разложение заданной несимметричной системы на симметричные составляющие; расчёт токов каждой из последовательностей в отдельности; суммирование токов всех последовательностей.
Расчёт аварийных режимов (КЗ, обрыв фазы) симметричных цепей производится следующим образом: в месте аварии вводятся системы трёх несимметричных напряжений UA—UB—UC и трёх несимметричных токов IA—IB—IC. Каждая из этих систем раскладывается на симметричные составляющие U1—U2—U0, I1—I2—I0. Далее рассматриваются схемы прямой, обратной и нулевой последовательностей, для каждой из которых составляются уравнения, связывающие U1 с I1, U2 с I2 и U0 с I0. Еще три уравнения составляются для аварийного участка и их вид определяется видом аварии. Решение этих уравнений даёт U1, U2, U0, I1, I2, I0, через которые могут быть определены все интересующие нас величины.
ЗАДАЧА 4.26. При соединении вторичных обмоток силового трёхфаз-ного трансформатора неверно были определены начало и конец обмотки BY. В результате соединения обмоток в звезду (рис. 4.33,а) система ЭДС приняла вид рис. 4.33,б.
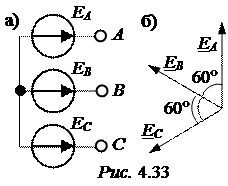
Найти симметричные составляющие представленной несимметричной системы, если EA = EB = EC = 220 B.
Решение
Составляющая нулевой последовательности
E0= (EA + EB + EC) = (220 + 220×e j 60 ° + 220×e j 120 ° ) = 
×e j 60 ° = 146,7×e j 60 ° B.
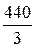
Составляющая прямой последовательности
E1= (EA + a×EB + a 2 ×EC), где a = e j 120 ° , откуда
E1= 
(1 + e j 120 ° ×e j 60 ° + e -j 120 ° ×e j 120 ° ) = = 73,33 B.
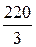
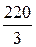
Составляющая обратной последовательности
E2= (EA + a 2 ×EB + a×EC) = (1 + e –j 120 ° ×e j 60 ° + e j 120 ° ×e j 120 ° ) = 146,7×e -j 60 ° B.
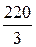
Проверим результат разложения векторов на симметричные составляющие:
|
|
|
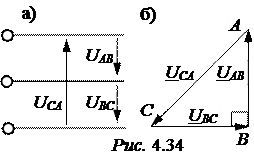
ЗАДАЧА 4.27. Из-за неравномерной нагрузки в конце трёхфазной трёхпроводной линии (рис. 4.34,а) напряжения образуют прямоугольный треугольник (рис. 4.34,б), катеты которого UAB = UBC = 360 B, причём синусоида линейного напряжения UAB имеет начальную фазу на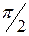 
больше синусоиды напряжения UBC.
Определить симметричные составляющие несимметричной системы линейных напряжений. Найти коэффициент несимметрии.
Решение
Так как линейные напряжения образуют замкнутый контур, то
= -360×(1 – j) = 360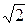 
×e j 135 ° B.
Составляющая нулевой последовательности в линейных напряжениях отсутствует, так как U0= (UAB + UBC + UCA) = ×0 = 0.
Составляющая прямой последовательности
U1= (UAB + a×UBC + a 2 ×UCA) = (360 + e j 120 ° ×360×e –j 90 ° + e -j 120 ° ×360 ×e j 135 ° ) =
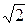
Составляющая обратной последовательности
U2= (UAB + a 2 ×UBC + a×UCA) = 
(1 + e –j 120 ° ×e –j 90 ° + e j 120 ° × ×e j 135 ° ) =
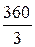
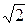
Коэффициент несимметрии k =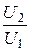 
= 
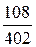
= 0,269 или k = 26,9%.
Заметим, что по Правилам технической эксплуатации установок потребителей (ПТЭ) степень несимметрии (коэффициент несимметрии) не должна превышать 4%.
ЗАДАЧА 4.28. К системе напряжений задачи 4.27 подключен соеди-нённый звездой асинхронный трёхфазный двигатель, каждая фаза которого имеет сопротивления: при прямом порядке чередования фаз Z1= 8 + j6 Ом, при обратной последовательности – Z2= 4,5 + j1 Ом. Найти токи в фазах двигателя.
Решение
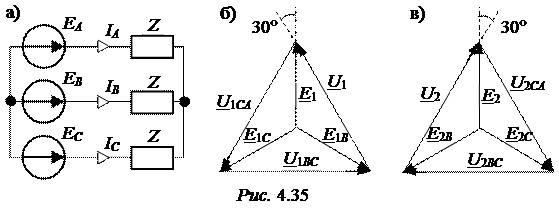
Представим, что двигатель подключен к несимметричному генератору, а обмотки последнего соединены в звезду (рис. 4.35,а).
Рассчитаем симметричные составляющие фазных ЭДС несимметричного генератора, используя ранее найденные симметричные составляющие линейных напряжений U1 и U2 и их соотношения, представленные на векторных диаграммах рис. 4.35,б и 4.35,в:
E1 =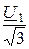 
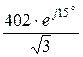
×e – j 30 ° = 
×e – j 30 ° = 232×e – j 15 ° В;
E2 =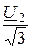 
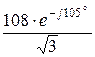
×e j 30 ° = 
×e j 30 ° = 62,4×e – j 75 ° В.
ЭДС несимметричного генератора выражаются через их симметричные составляющие: EА = E1 + E2 = 232×e – j 15 ° + 62,4×e – j 75 ° = 268,7×e – j 26,60 ° В,
 |
В результате проведенного преобразования источника ЭДС (последовательное соединение двух симметричных систем ЭДС – прямой и обратной последовательностей) схема в отношении симметричных составляющих симметрична и рассчитывается по методу наложения.
Расчёт тока прямой последовательности:
I1 =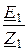 
= 
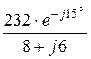
= 23,2×e – j 51,87 ° А.
Расчёт тока обратной последовательности:
I2 =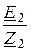 
= 
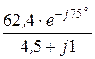
= 13,54×e – j 87,53 ° А.
Токи в фазах двигателя рассчитаем с учётом того, что в трёхфазной трёхпроводной системе составляющие токов нулевой последовательности (I0 =0) отсутствуют:
ЗАДАЧА 4.29. Двигатель зада-чи 4.28 был подключен к симметрич-ной трёхфазной цепи с линейным напряжением U = 380 B. В цепи про-изошёл обрыв линейного провода С.
Выполнить тот же расчёт, что и в задаче 4.27 для новых условий работы двигателя.
Решение
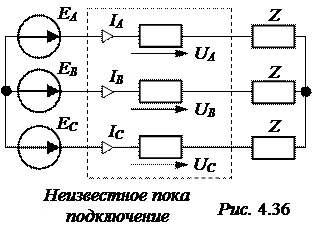
В симметричной трёхфазной цепи произошло продольное нарушение симметрии, что может трактоваться как последовательное подключение несимметричного приёмника с пока неизвестными напряжениями UА, UВ, UС и токами IА, IВ, IС. Расчётная схема новых условий работы двигателя представлена на рис. 4.36.
Отметим, что в фазах неизвестного пока подключения могут содержаться как пассивные, так и активные элементы цепи.
Выполним формальное разложение несимметричных систем напряжений и токов подключения на симметричные составляющие.
U0= (UA + UB + UC) I0= (IA + IB + IC),
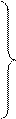
U1= (UA + a×UB + a 2 ×UC) (1), I1= (IA + a×IB + a 2 ×IC),
U2= (UA + a 2 ×UB + a×UC) I2= (IA + a 2 ×IB + a×IC).
Определим симметричные составляющие заданной системы ЭДС генератора: по условию она остаётся симметричной, прямой последовательности при нарушении симметричного режима работы схемы. Симметричная система ЭДС не содержит составляющих обратной и нулевой последовательности, то есть для ЭДС EA, EB, EC получаем:
E2= E0= 0; E1=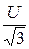 
= 
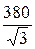
= 220 B.
В отношении симметричных составляющих вся схема становится симметричной и её расчёт можно вести по схемам замещения для одной фазы применительно к каждой системе.
 |
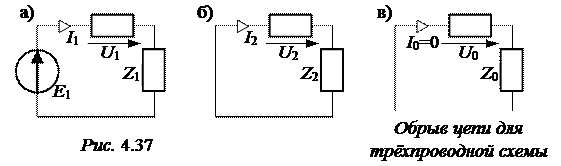Схема замещения для тока прямой последовательности приведена на рис. 4.37,а, для тока обратной последовательности – на рис. 4.37,б, для тока нулевой последовательности – на рис. 4.37,в.
В соответствии с законами Кирхгофа для схем замещения получаем 3 уравнения для определения шести симметричных составляющих неизвест-ных напряжений и токов:
Недостающие уравнения получим, исходя из характеристики несимметричности участка в соответствии с рис. 4.38 при обрыве линейного провода С:
; 
; UС ¹ 0;
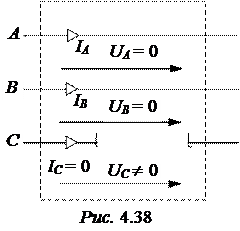
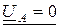
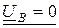
IА ¹ 0; IВ ¹ 0;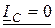 
.
Три подчеркнутых уравнения определённые. Перепишем их, заменив UА, UВ, IС их симметричными составляющими (пока неизвестными):
UA = U0+ U1+ U2= 0;
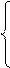
Из системы (1) с учётом того, что
U0= UС, U1= a 2 ×UС, U2= a×UС, откуда 
= a. (4)
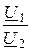
Учтём, что I0= 0. На основании (3) получаем
Оставшиеся уравнения (2) представим в виде
= 
= a, а с учётом (5) 
= a.
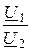
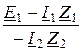
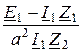
I1 =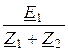 
= 
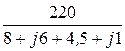
= 15,4×e –j 29,25 ° А,
Видео:Метод симметричных составляющих - трехфазные цепи, часть 1Скачать
Метод симметричных составляющих
Содержание:
Метод симметричных составляющих:
Метод расчета несимметричных режимов трехфазных цепей, относился к частным случаям таких режимов, когда не было взаимной индукции между фазами или она могла быть учтена в эквивалентном сопротивлении на фазу (при отсутствии нейтрального провода не было вращающихся машин с несимметричным ротором, отсутствовали токи в земле с неизбежным индуктивным влиянием на фазные обмотки или провода.
Для расчета несимметричных режимов трехфазных электрических цепей в общем случае применяется метод симметричных составляющих, основанный на представлении любой трехфазной несимметричной системы электрических или магнитных величин (токов, напряжений, магнитных потоков) в виде суммы трех симметричных систем. Эти симметричные системы величин, образующих в совокупности несимметричную систему, носят название симметричных составляющих прямой, обратной и нулевой последовательностей. При этом под последовательностью подразумевается порядок следования во времени максимумов фазных величин.
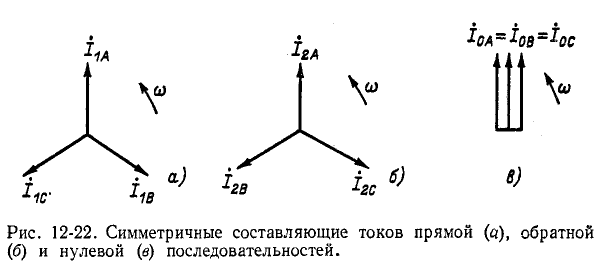
На рис. 12-22 в виде примера показаны симметричные составляющие токов всех трех последовательностей. Как видно из рисунка, симметричные составляющие обозначаются цифрами 1, 2, 0. 
Система прямой последовательности образует симметричную трехлучевую звезду 
Система обратной последовательности образует трехлучевую звезду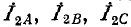 
с порядком следования фаз А, С, В.
Система нулевой последовательности состоит из трех равных векторов: 
Векторами, показанными на рис. 12-22, могут изображаться как комплексные амплитуды, так и комплексные действующие значения токов трех последовательностей.
Мгновенные (синусоидальные) значения симметричных составляющих мыслятся в виде проекций на мнимую ось комплексных амплитуд, вращающихся с угловой скоростью со в положительную сторону. Следует обратить внимание на то, что направление вращения у всех трех систем векторов одно и то же.
Взаимное расположение и модули векторов прямой, обратной и нулевой последовательностей зависят от характера несимметрии и электрических параметров трехфазной цепи.
На основании рис. 12-22: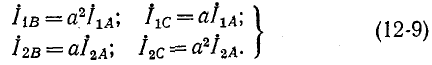 
Токи в фазах А, В и С определяются как суммы соответствующих симметричных составляющих:
В дальнейшем ради упрощения записи индекс Л при симметричных составляющих фазы A опущен, т. е.
С учетом (1^-9) и (12-11) выражения (12-10) принимают вид:
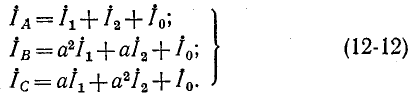
Эти формулы служат для нахождения фазных токов по их симметричным составляющим.
Если известны фазные токи, то симметричные составляющие служат решением системы уравнений (12-12). Умножив вторую стр.оку на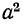 
и третью строку на сг и сложив уравнения (12-12), получим (с учетом того, что
Аналогичным образом, умножив вторую строку на а-и третью строку на а и сложив уравнения (12-12), найдем:
Наконец, сложив уравнения (12-12), получим:
Выражения (12-12) — (12-15) являются общими; они применимы также для напряжений, магнитных потоков и других величин.
Видео:Метод симметричных составляющих (виртуальная лаборатория РЗА - опыт 1)Скачать
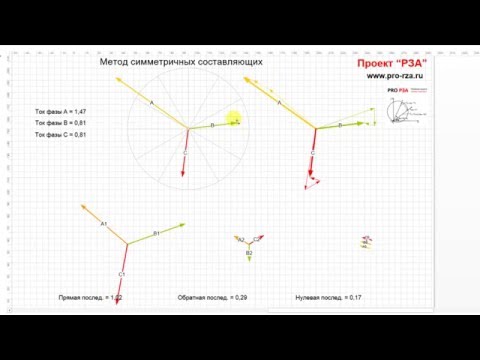
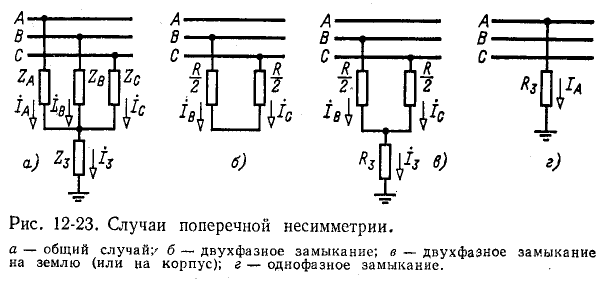
Поперечная несимметрия
Поперечная несимметрия в одной точке трехфазной цепи возникает в том случае, когда к фазам присоединяются неравные сопротивления, как это, например, показано на рис. 12-23, а. Такое включение может иметь место при несимметричном коротком замыкании или несимметричной нагрузке.
Любые два сопротивления из числа включенных в звезду, а также сопротивление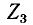 
могут быть равны нулю или бесконечности. Таким образом, различные виды несимметрии или короткого замыкания, изображенные, например, на рис. 12-23, б, в иг, получаются как частные случаи из общего случая, представленного на рис. 12-23, а.
В случае короткого замыкания сопротивления в месте замыкания складываются из сопротивлений электрических дуг и заземлений. Эти сопротивления, как показали экспериментальные исследования, являются активными. Поэтому сопротивления для упомянутых выше частных случаев приняты активными, а именно:
1) при двухфазном замыкании между фазами В и С (рис. 12-23, б)
2) при двухфазном замыкании на землю (или корпус самолета) (рис. 12-23, в)
3) при однофазном замыкании на землю (корпус) (рис. 12-23, г)
Поперечная несимметрия в общем случае (рис. 12-23, а) характеризуется уравнениями: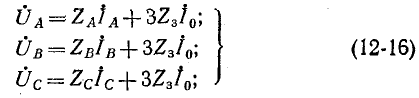 
здесь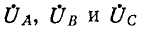 
— фазные напряжения в месте несим-метрии относительно земли.
Входящие в (12-16) фазные напряжения и токи могут быть с учетом формул (12-12) заменены симметричными составляющими. При этом получаются три уравнения, связывающие симметричные составляющие в месте поперечной несимметрии (так называемые граничные условия).
Дополнительные три уравнения, необходимые для вычисления шести неизвестных (симметричных составляющих напряжений и токов в месте несимметрии), даются соотношениями между напряжениями и токами одноименных последовательностей для фазы А: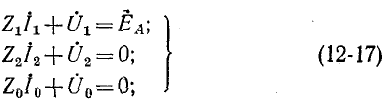 
здесь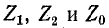 
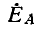
— результирующие фазные сопротивления всей цепи (без сопротивлений в месте несимметрии) для токов прямой, обратной и нулевой последовательностей; 
— э. д. с. фазы А эквивалентного генератора.
Формулы (12-17) выражают второй закон Кирхгофа для каждой последовательности в отдельности. Поскольку э. д. с. генератора трехфазного тока образует симметричную звезду с прямым чередованием фаз, в уравнениях (12-17) э. д. с. генератора входит только в уравнение для составляющих прямой последовательности; в остальных двух уравнениях, связывающих составляющие напряжений и токов обратной и нулевой последовательностей, э. д. с. генератора отсутствует.
Сопротивления прямой, обратной и нулевой последовательностей для электрических машин (генераторов, электрических двигателей, трансформаторов) берутся по заводским данным.
Равенство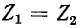 
имеет место только для статических не вращающихся устройств — трансформаторов, линий и т. п.
Для вращающихся электрических машин обычно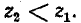 
Разница в сопротивлениях прямой и обратной последовательностей электрических машин обусловлена различными направлениями вращения магнитных полей, образуемых токами прямой и обратной последовательностей: направление вращения магнитного поля, созданного токами прямой последовательности, совпадает с направлением вращения ротора, магнитное же поле, образованное токами обратной последовательности, вращается в противоположную сторону. Более подробно этот вопрос рассматривается в литературе по электрическим машинам и токам короткого замыкания в трехфазных системах.
Сопротивления прямой и нулевой последовательностей трехфазной линии (кабельной или воздушной) находятся расчетным или опытным путем, причем сопротивления прямой и обратной последовательностей для линий одинаковы, а сопротивление нулевой последовательности может в 2—3 раза превышать сопротивление прямой последовательности. Объясняется это различием э. д. с. взаимной индукции, наводимых в фазе токами прямой и нулевой последовательностей, протекающими по двум другим фазам, а также сопротивлением земли или обшивки транспортного средства, по которому проложена сеть.
Методика определения симметричных составляющих токов и напряжений и построения’ соответствующих векторных диаграмм иллюстрирована ниже на примере частных случаев поперечной несимметрии.
1. Двухфазное короткое замыкание (рис. 12-23, б). Граничные условия удовлетворяют уравнениям: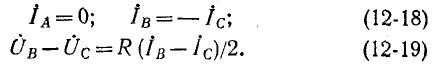 
Подстановка (12-18) в (12-13) и (12-14) дает:
откуда
Подстановка (12-18) в (12-15) дает: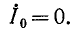
Кроме того, на основании (12-19) 
или
Уравнения (12-20) и (12-21) вместе с дополнительными первыми двумя уравнениями (12-17) достаточны для нахождения четырех неизвестных: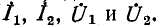 
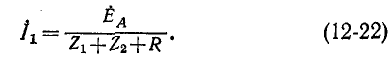
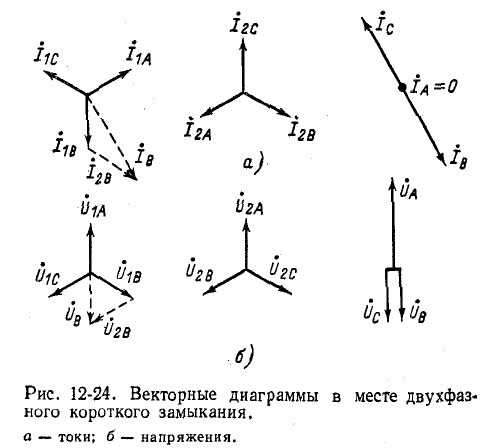
В результате совместного решения этих уравнений получается: 
На рис. 12-24 представлены векторные диаграммы токов и напряжений в месте двухфазного короткого замыка-
ния при R = 0 (металлическое короткое замыкание). В этом случае в соответствии с (12-21) 
Векторные диаграммы построены в предположении, что вектор э. д. с. ЁА направлен вертикально вверх, причем углы комплексных сопротивлений прямой и обратной последовательностей одинаковы (например, 60°). Поэтому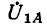 
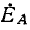
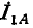
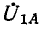
совпадает по фазе с 
и ток 
отстает от 
на заданный угол.
Сумма токов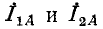 
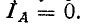
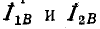
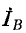
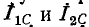
в месте двухфазного короткого замыкания равна нулю, поэтому 
Токи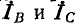 
дают в сумме фазный ток 
в месте короткого замыкания, а токи 
дают в сумме фазный ток 
Токи 
находятся в противофазе.
Поскольку при построении векторных диаграмм сопротивление R в месте короткого замыкания принято равным нулю, фазные напряжения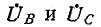 
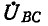
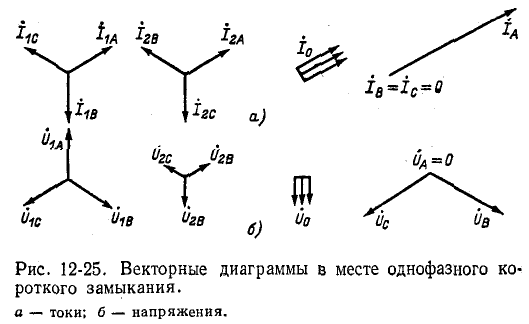
в месте повреждения равны друг другу и соответственно линейное напряжение 
равно нулю. По мере удаления от места короткого замыкания в сторону генератора линейное напряжение между фазами В и С возрастает.
2. Однофазное короткое замыкание (см. рис. 12-23, г). Граничные условия удовлетворяют уравнениям:
Замена фазных величин их симметричными составляющими дает: 
В результате совместного решения уравнений (12-17) и (12-23) получается: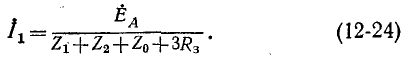 
Векторные диаграммы токов и напряжений при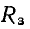 
= О представлены на рис. 12-25.
Видео:Несимметричные КЗ. Вектора и вектор аСкачать
Продольная несимметрия
Продольная несимметрия в одной точке трехфазной цепи возникает в том случае, когда в рассечку фаз включаются неравные сопротивления, как это, например, показано на рис. 12-26, а. Любые два сопротивления могут быть при этом равны нулю или бесконечности.
Продольная несимметрия характеризуется в данном случае уравнениями: 
здесь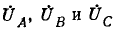 
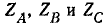
— напряжения на выводах сопротивлений 
(продольные напряжения).
В результате замены напряжений и токов, входящих в (12-25), симметричными составляющими получаются три уравнения (граничные условия), связывающие симметричные составляющие в месте продольной несимметрии.
В частном случае, изображенном на рис. 12-26, б,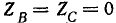 
и соответственно
Симметричные составляющие продольных напряжений
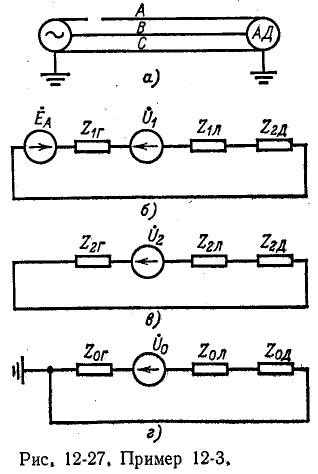
Пример 12-3. К трехфазному генератору присоединена линия с асинхронным двигателем на конце (рис. 12-27, а). Нейтральные точки генератора и двигателя заземлены, Произошел обрыв фазы А вблизи выводов генератора. Требуется определить токи в фазах В и С и напряжения в месте обрыва.
Обозначим: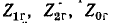 
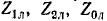
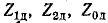
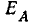
— комплексные сопротивления прямой, обратной и нулевой последовательностей генератора; 
— то же для линии; 
— то же для асинхронного двигателя;
— э. д. с. фазы А генератора.
Для сокращения записи обозначим:
На основании схем замещения для отдельных последовательностей (рис, 12-27, б — а) можно написать основные уравнения (12-17):
Для данного случая добавочные уравнения согласно (12-26) при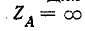 
будут:
Совместное решение этих уравнений дает:
где
Полные токи и напряжения могут быть легко найдены суммированием отдельных составляющих.
Видео:Электротехника. ТОЭ 74. Вектора трёхфазной системы, прямая, нулевая и обратная последовательности.Скачать
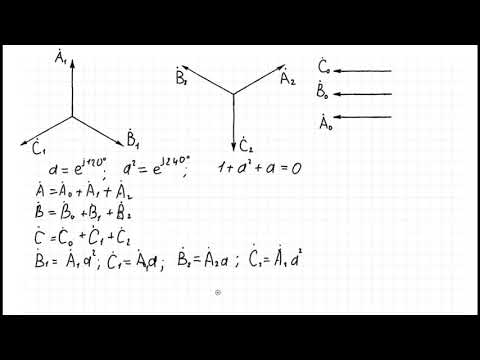
Фильтры симметричных составляющих
Фильтрами симметричных составляющих называются устройства, служащие для выделения соответствующих составляющих напряжений или токов трехфазной цепи. Фильтры имеют входные и выходные выводы. К входным выводам фильтра подводятся напряжения или токи трехфазной электрической цепи; на выходных выводах фильтра получается напряжение или ток, пропорциональные соответствующим симметричным составляющим электрических величин, подводимых к входным выводам.
Напряжения и токи, выделяемые фильтрами симметричных составляющих, используются на практике для цепей автоматики, защиты от несимметричных режимов или сигнализации. С этой целью к выходным выводам фильтров симметричных составляющих присоединяются соответствующие аппараты, приборы, реле и т. п.
Наиболее простой тип фильтра симметричных составляющих представляет собой фильтр токов нулевой последовательности, в котором суммируются токи трех фаз (рис. 12-28, а) или создаваемые ими магнитные потоки (рис. 12-28, б). В первом случае реагирующий прибор включается в нейтральный провод трех
трансформаторов тока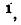 
а во втором случае — Между выводами обмотки; насаженной на магнитопровод, охватывающий три фазы.
Фильтр напряжений нулевой последовательности выполняется с помощью трех однофазных трансформаторов напряжения, первичная обмотка которых соединяется звездой с выведенной нейтральной точкой, а вторичная обмотка соединяется разомкнутым треугольником (рис. 12-28, в).
Благодаря такому соединению составляющие напряжений прямой последовательности взаимно компенсируются: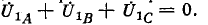 
То же имеет место и в отношении напряжений обратной последовательности: 
Составляющие же напряжений нулевой последовательности образуют на выводах разомкнутого треугольника напряжения 
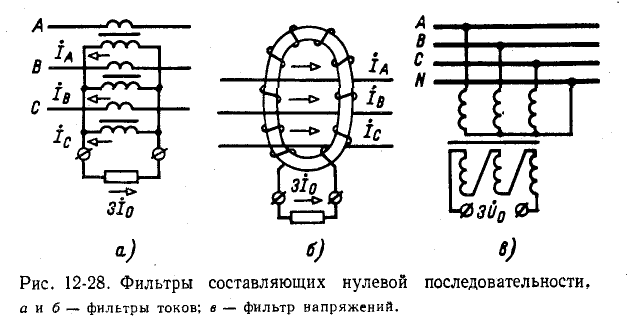
Фильтр напряжений нулевой последовательности может быть получен и с помощью трех равных сопротивлений, соединенных звездой и приключенных к трехфазной цепи. При симметричном режиме работы трехфазной цепи напряжение между нейтральной точкой этих сопротивлений и нейтральной точкой цепи равно нулю; при появлении же в трехфазной цепи составляющих напряжений нулевой последовательности между упомянутыми точками возникает напряжение, пропорциональное составляющей нулевой последовательности.
Системы симметричных составляющих прямой и обратной последовательностей различаются порядком следования во времени амплитуд фазных величин, поэтому всякая схема для выделения составляющих обратной последовательности может быть путем перестановки любых двух фаз превращена в схему для выделения составляющих прямой последовательности. С этой точки зрения является достаточным рассмотреть фильтры только какой-либо одной из указанных последовательностей, например обратной, распространив затем полученные результаты на фильтры симметричных составляющих другой (прямой) последовательности.
Вторичные токи трансформаторов тока приближенно равны первичным, деленным на отношение чисел витков 
На рис. 12-28 вторичные токи и напряжения приведены к первичной обмотке.
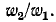
Принцип выполнения фильтров токов и напряжений обратной последовательности иллюстрирован ниже на примере двух схем: схемы фильтра токов трансформаторного типа (рис. 12-29) и схемы четырехэлементного активно-емкостного фильтра напряжений (рис. 12-30).
В фильтрах обоих типов суммируются напряжения, находящиеся в определенных соотношениях с токами или напряжениями, подводимыми к входным выводам фильтров.
Фильтр токов обратной последовательности, изображенный на рис. 12-29, состоит из активных сопротивлений, между которыми проложен нейтральный провод трансформаторов тока, и промежуточного трансформатора, токовые обмотки которого в фазах В и С связаны индуктивно с третьей обмоткой в выходной цепи; параметры фильтра удовлетворяют условию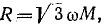 
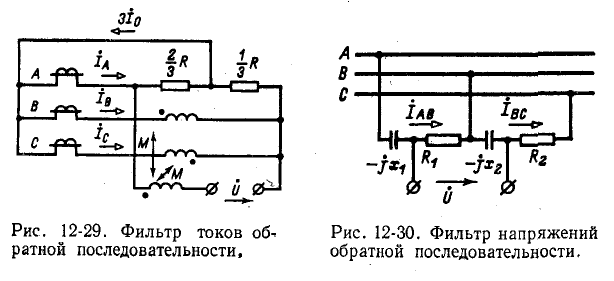
где
— угловая частота тока, на которую рассчитан фильтр; М — взаимная индуктивность первичной и вторичной обмоток промежуточного трансформатора.
Благодаря тому, что магнитопровод промежуточного трансформатора имеет воздушный зазор, обеспечивается линейная зависимость э. д. с. взаимной индукции от токов.
Напишем уравнение второго закона Кирхгофа по выходному контуру:
С учетом первого закона Кирхгофа
и соотношений между симметричными составляющими
т. е. выходное напряжение пропорционально току обратной последовательности.
Влияние токов нулевой последовательности отсутствует в рас-сматриваемом фильтре благодаря взаимной компенсации падений напряжения оттоков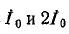
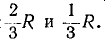
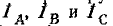
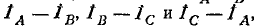
в сопротивлениях 
Другой возможный способ устранения влияния токов нулевой последовательности заключается в том, что к фильтру токов обратной последовательности вместо фазных токов 
подводятся разности фазных токов 
в которых составляющие нулевой последовательности отсутствуют.
Аналогичным образом для устранения влияния напряжений нулевой последовательности фильтры напряжений обратной последовательности включаются обычно на линейные напряжения 
На рис. 12-30 показан четырехэлементный фильтр напряжений обратной последовательности, применяемый в релейной защите. Параметры элементов фильтра подбираются из условия
При холостом режиме работы фильтра, т. е. при разомкнутых вторичных выводах, напряжение на этих выводах равно сумме
Если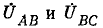 
выразить через симметричные составляющие линейных напряжений, то напряжение на выходных выводах фильтра будет равно:
т. е. пропорционально составляющей обратной последовательности. Если на выходе фильтра присоединена нагрузка (реагирующий прибор), то ток или напряжение в выходной цепи могут быть получены на основании теоремы об эквивалентном источнике.
Пример 12-4. К выходным выводам фильтра токов обратной последовательности, показанного на рис, 12-29, подключена нагрузка
Определить ток в нагрузке при подведений к входным выводам фильтра системы несимметричных токов.
Будем исходить из предположения, что к выходным выводам фильтра подключены источники токов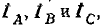 
так как эти токи ие зависят от сопротивлений нагрузки.
Согласно (12-27) напряжение на разомкнутых выходных выводах фильтра равно 
По теореме об эквивалентном источнике ток в нагрузке равен:
где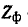
— сопротивление фильтра, измеренное со стороны его выходных выводов при разомкнутых входных выводах, так как внутренние сопротивления источников тока равны бесконечности.
Обозначив через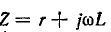 
сопротивление вторичной обмотки промежуточного трансформатора, включенной в выходную цепь, получим:
Таким образом, при заданном значении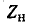 
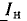
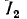
пропорциональность тока 
току 
сохраняется.
Пример 12-5. К выходным выводам фильтра напряжений обратной последовательности, показанного на рис. 12-30, подключена нагрузка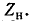 
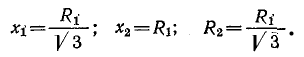
Параметры элементов фильтра, удовлетворяющие соотношению (12-28), выбраны следующим образом: 
Определить напряжение на нагрузке при подведении к входным выводам фильтра несимметричных напряжений.
Будем исходить из предположения, что к входным выводам фильтра подключены источники э. д. с.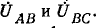 
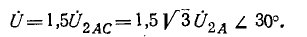
Согласно»(12-29)напряжение на разомкнутых выходных выводах фильтра равно:
По теореме об эквивалентном источнике напряжение на нагрузке равно: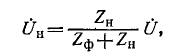 
где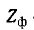 
— сопротивление фильтра, измеренное со стороны его выходных выводов при закороченных входных выводах, так как внутренние сопротивления источников э. д. с. равны нулю.
Следовательно, в соответствии с заданием
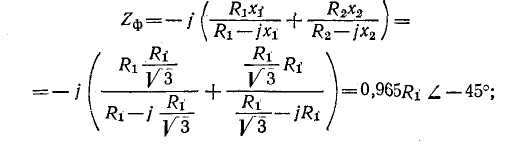
отсюда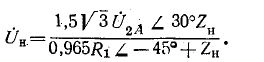 
При любом заданном значении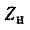 
сохраняется пропорциональность между 
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Цепи периодического несинусоидального тока
- Резонанс токов
- Трехфазные симметричные цепи
- Трехфазные несимметричные цепи
- Электрические цепи с взаимной индуктивностью
- Резонанс в электрических цепях
- Соединение звездой и треугольником в трехфазных цепях
- Принцип действия асинхронного и синхронного двигателей
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎥 Видео
Двухфазное КЗ на векторных диаграммахСкачать
Метод симметричных составляющих - Часть 2Скачать
Метод симметричных составляющих при различных видах несимметричного короткого замыкания.Скачать
2.6. НесимметрияСкачать
10-1 Метод симметричных составляющих для расчета несимметричных КЗСкачать
Лапидус А.А. Метод симметричных составляющихСкачать
Как разложить вектор по базису - bezbotvyСкачать
Как решать задачи Методом симметричных составляющих, часть 3. Трехфазные цепиСкачать
ЭМПП Лекция 4Скачать
Измерение мощности в трёхфазных цепях. Метод симметричных составляющих (Преобразование Форбескью).Скачать
ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать
Двухфазное КЗСкачать
Теоретические основы электротехники. Струмеляк А.В.Скачать
Лапидус А.А. Метод симметричных составляющих. ПримерСкачать
10-2 Составление схем замещения и расчет несимметричного ТКЗСкачать
