Объём параллелепипеда равен смешанному произведению векторов на которых он построен:
Поскольку смешанное произведение векторов, может быть отрицательным числом, а объём геометрического тела — всегда число положительное, то при вычислении объёма параллелепипеда, построенного на векторах, результат смешанного произведения берется по модулю:
Таким образом, для того, чтобы вычислить объём параллелепипеда, построенного на векторах, нужно найти смешанное произведение данных векторов, и полученный результат взять по модулю.
Наш онлайн калькулятор, найдет площадь параллелепипеда с описанием подробного хода решения на русском языке.
Видео:Вычисляем высоту через координаты вершин 1Скачать

Задача 61425 Объём параллелепипеда, построенного на.
Условие
Объём параллелепипеда, построенного на векторах a, b, c, равен V = 12.
Площадь параллелограмма, построенного на векторах a, b, равна S = 3. Найти высоту
параллелепипеда, построенного на векторах 2a + b, a − b, a + b + 4c, которая опущена из
конца третьего вектора на грань, построенную на первых двух.
Решение
По условию:
S_(данного параллелограмма)=3 ⇒[m] |[vec × vec]|=3[/m]
Найдем векторное произведение:
Найдем смешанное произведение
V_( параллелепипеда)=S_( основания )*Н=S_( параллелограмма)*Н
Видео:§20 Нахождение объёма параллелипипедаСкачать

Смешанное, векторное и скалярное произведение векторов
Задача:
Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).
Найти:
Решение:
- а) Объем параллелепипеда будем искать через смешанное произведение векторов (AB AD AA1). Мы знаем, что модуль смешанного произведения векторов равен объему параллелепипеда, построенному на этих векторах.
| (AB AD AA1) | = |
| = | 20 — 18 + 0 — 0 — 30 + 16 | = | -12 | . |
|---|
Мы нашли смешанное произведение, ещё надо его взять по модулю и найдём объем параллелепипеда:
VABCDA1B1C1D1=12.
б) Площадь, как мы уже знаем, можно искать через векторное произведение векторов. Грань ABCD построена на векторах AB и AD, найдём их векторное произведение. SABCD= |[AB AD]|.
| [AB AD] | = |
| = | 6i — 8j — 2k | , |
|---|
Теперь найдём модуль этого вектора:
| SABCD= |[AB AD]|=√ | (36+64+4) | =2√(26). |
|---|
| [AD AA1] | = |
| = | 9i — 16j — k | , |
|---|
SADD1A1= |[AD AA1]|=√(81+256+1)=13√2.
| h | = |
| = |
| = |
| = |
| . |
|---|
| cos(λ1) | = |
| . |
|---|
Координаты вектора AB мы имеем, от вектор B1D надо найти. Для этого используем следующую формулу:
B1D = B1A1 + A1A + AD = — AB — AA1 + AD1 = — (4, 3, 0) — (-3, -2, 5) + (2, 1, 2); (Не забывайте, что всё это векторы, надо сложить их соответствующие координаты. )
Сделав вычисления по этой формуле, мы найдём, что вектор B1D имеет координаты (1, 0, -3). Теперь надо найти длину векторов AB и B1D:
|AB|=√(16+9+0)=5, |B1D|=√(1+0+9)=√(10).
Найдём скалярное произведение векторов AB и B1D, (AB B1D)=4*1 + 3*0 + 0*(-3)=4.
Теперь, имея все данные мы можем подставить их в нашу формулу:
| cos(λ1) | = |
| = |
| . |
|---|
д) Что бы найти cos(λ2), мы используем то, что угол между двумя плоскостями равен углу между перпендикулярами до этих плоскостей. А как мы знаем, векторное произведение — это и есть перпендикуляр до плоскости перемножаемых векторов. Поэтому в роле перпендикуляра к плоскости ADD1A1 мы можем взять вектор [AD AA1], который мы нашли в пункте б), и знаем, что его координаты (9, -16, -1), точно также и для плоскости ABCD — вектор [AB AD] с координатами (6, -8, -2).
Теперь нам остаётся, как в предыдущем варианте найти только косинус угла между двумя векторами, координаты которых нам известны.
| cos(λ2) | = |
| = |
| . |
|---|
Вот таким не хитрым способом мы и нашли косинус угла между гранями ABCD и ADD1A1.
🔍 Видео
Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

1. Векторы и параллелограмм задачи №1Скачать

Правило параллелепипеда для векторовСкачать

Площадь параллелограмма, построенного на данных векторахСкачать

Решение, найти высоту параллелепипеда, построенного на векторах a, b, c пример 17 Высшая математикаСкачать

Площадь параллелограмма по векторамСкачать

Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

Вычисление медианы, высоты и угла по координатам вершинСкачать

координаты вектора AH, который перпендикуляр из точки A к основанию параллелепипедаСкачать

Координаты вектора в пространстве. 11 класс.Скачать

Задача 6 №27612 ЕГЭ по математике. Урок 62Скачать

Решение, найти высоту параллелепипеда, построенного на векторах a, b, c пример 18 Высшая математикаСкачать

Площадь треугольника, построенного на векторахСкачать

Найдите площадь параллелограмма, построенного на векторахСкачать

КАК НАЙТИ ВЫСОТУ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА, ЕСЛИ ИЗВЕСТЕН ОБЪЕМ, ДЛИНА И ШИРИНА? Пример 5 классСкачать

Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

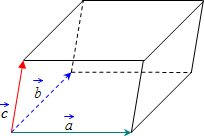
 Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).
Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).