Как перейти в полярную систему координат из интеграла окружности (5 видео)

Двойные интегралы в полярных координатах: теория и примеры

Содержание

Что значит вычислить двойной интеграл в полярных координатах?
Пределы интегрирования в повторных интегралах
Случай первый
Случай второй
Случай третий
Случай четвёртый
Решения двойных интегралов в полярных координатах: примеры
Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам
Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам
Далее:
Презентация к защите
🎬 Видео

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Что значит вычислить двойной интеграл в полярных координатах?

Если область интегрирования представляет собой окружность или часть окружности, двойной интеграл проще вычислить не в декартовых прямоугольных координатах, а в полярных координатах. В этом случае подынтегральная функция выражается как функция полярных переменных r и φ с использованием соотношений между полярными и декартовыми координатами x = rcosφ и y = rsinφ :

Что представляет собой элемент площади dxdy , выраженный в полярных координатах? Для ответ на этот вопрос разделим область интегрирования D на участки линиями окружности r = const и лучами φ = const . Рассмотрим один частичный участок (заштрихованный на рисунке), который ограничивают лучи, образующие с полярной осью углы φ и φ + dφ и линии окружности с радиусом r и r + dr . Этот криволинейный четырёхугольник можем приближенно считать прямоугольником с длиной боковой стороны dr и длиной основания rdφ . Поэтому элемент площади в полярных координатах выражается следующим образом:

а двойной интеграл в полярных координатах записывается так:

Чтобы вычислить двойной интеграл в полярных координатах, его нужно выразить через повторные интегралы, так же, как и «обычный» двойной интеграл в декартовых прямоугольных координатах. В полярных координатах внешний интеграл всегда интегрируется по углу φ , а внутренний — по радиусу r .

Вычислить двойной интеграл в полярных координатах — значит, как и в декартовых прямоугольных координатах, найти число, равное площади упомянутой фигуры D .

Видео:Двойной интеграл в полярных координатахСкачать

Пределы интегрирования в повторных интегралах

При переходе от двойного интеграла в полярных координатах к повторным интегралам расстановку пределов интегрирования могут облегчить следующие закономерности.

Случай первый

Полюс O является внутренней точкой области интегрирования D , область ограничена линией r = r(φ) .

Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны 0 и 2π , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай второй

Полюс O находится на границе области интегрирования D , ограниченного линией r = r(φ) , но не является угловой точкой.

Через полюс O проведём касательную. Пусть касательная образует с полярной осью угол α . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и π + α , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай третий

Полюс O находится на границе области интегрирования D , ограниченного линией r = r(φ) , и является угловой точкой.

Из полюса O проведём лучи, которые будут ограничивать область D . Пусть эти лучи образуют с полярной осью углы α и β . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай четвёртый

Полюс O находится вне области интегрирования D .

Из полюса O проведём лучи, которые будут ограничивать область D . Пусть эти лучи образуют с полярной осью углы α и β , а область D ограничивают линии r = r 1 (φ) и r = r 2 (φ) . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β , а внутреннего интеграла — r 1 (φ) и r 2 (φ) . Переход к повторным интегралам осуществляется следующим образом:

Видео:Площадь фигуры через двойной интеграл в полярных координатахСкачать

Решения двойных интегралов в полярных координатах: примеры

Пример 1. Вычислить в полярных координатах двойной интеграл

где область D ограничена линиями , , .

Решение. Строим на чертеже область интегрирования. Видим, что этот пример относится к третьему случаю из вышеописанных четырёх случаев расположения области интегрирования.

Выразим подынтегральную функцию как функцию полярных переменных:

Данные в условии линии, ограничивающие D , приводим к полярным координатам:

Переходим от двойного интеграла к повторному, учитывая пределы интегрирования, верные в третьем случае:

Вычисляем интеграл (так как повторные интегралы независимы друг от друга, каждый из них вычисляем отдельно и результаты перемножаем):

Пример 2. В повторном интеграле

перейти к полярной системе координат.

Решение. В повторном интеграле переменная x изменяется от -1 до 1, а переменная y — от параболы x² до 1. Таким образом, область интегрирования снизу ограничена параболой y = x² , а сверху — прямой y = 1 . Область интегирования изображена на следующем чертеже.

При переходе к полярным координатам область интегрирования нужно разделить на три части. Значит, данный повторный интеграл должен быть вычислен как сумма трёх интегралов. В первой области полярный радиус меняется от 0 до параболы, во второй области — от 0 до прямой y = 1 , в третьей области — от 0 до параболы. Точки пересечения прямой y = 1 и параболы: (1; 1) и (−1; 1) . В первой точке полярный угол составляет , во второй точке он составляет . Поэтому в первой области φ меняется от от 0 до , во второй области — от 0 до , в третьей области — от до π .

Запишем линии, ограничивающие область интегрирования в полярной системе координат. Найдём уравнение прямой y = 1 : или . Найдём уравнение параболы y = x² в полярной системе координат:

Теперь у нас есть всё, чтобы от данного повторного интеграла перейти к полярным координатам:

Пример 3. Вычислить в полярных координатах двойной интеграл

где область D ограничена линией окружности .

Решение. Строим на чертеже область интегрирования.

Область интегрирования ограничивает линия окружности с центром в точке (a; 0) и радиусом a . В этом легко убедиться, преобразовав её уравнение следующим образом:

Линия окружности касается оси Oy , поэтому полярный угол в области интегрирования меняется от до . Подставим и в уравнение окружности и получим

Напишем подынтегральную функцию в полярных координатах:

Теперь можем перейти в данном двойном интеграле к полярным координатам:

Наконец, находим двойной интеграл в полярных координатах:

В полученном выражении второе слагаемое равно нулю, так как и sinπ , и sin(−π) равны нулю. Продолжая, получаем:

Пример 4. Вычислить плоской фигуры, которую ограничивают линии , , , .

Решение. Построим заданную фигуру на следующем рисунке.

Так как фигура является частью круга, её площадь проще вычислить в полярных координатах. Данные уравнения линий перепишем в полярных координатах:

Таким образом, у нас есть всё, чтобы записать площадь фигуры в виде двойного интеграл в полярных координатах, перейти к повторному интегралу и вычислить его:

Пример 5. Вычислить в полярных координатах двойной интеграл

где область D ограничена линиями и .

Решение. Преобразуем данные уравнения линий, чтобы было проще построить чертёж:

Строим на чертеже область интегрирования.

В данных уравнениях линий перейдём к полярным координатам:

В данном двойном интеграле перейдём к полярным координатам, затем к повторным интегралам и вычислим интеграл:

Видео:Полярная система координатСкачать

Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

Услуги проектирования
Двойной интеграл
Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

Видео:Построение кривой в полярной системе координатСкачать

Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

Смысл этих задач — научиться быстро определять параметры $a,;b,;varphi _1 (x),;varphi _2 (x),;c,;d,;psi _1 (y),;psi _2 (y)$ и $varphi _0 ,;varphi _2 ,;r_1 (varphi ),;r_2 (varphi )$ , необходимые для перехода от двойного интеграла к повторному.

Примеры:

Пусть область $D=left[right]cup left[right]$. Представить двойной интеграл по области $mathbf < textit > $ в виде повторных. Перейти к полярным координатам. 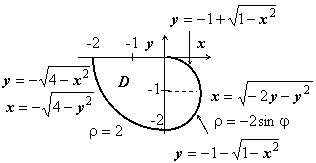Решение:

Область изображена на рисунке. Для левой части $D-2leqslant xleqslant 0;quad -sqrt leqslant yleqslant 0$; для правой — $0leqslant xleqslant 1,;-1-sqrt leqslant yleqslant -1+sqrt $ уравнение правой полуокружности после выделения полных квадратов принимает вид $x^2+(y+1)^2=1$, поэтому

Изменить порядок интегрирования, перейти к полярным координатам. 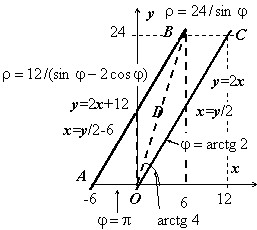$I=intlimits_ ^0 < dxintlimits_0^ > +intlimits_0^6 < dxintlimits_ ^ > +intlimits_6^ < dxintlimits_ ^ > $

Решение:

На рисунке изображена область и приведены уравнения прямых и обратных функций для линий, ограничивающих её. $mathbf < textit > $ можно представить в виде $D=left[right]$, поэтому $I=intlimits_0^ < dyintlimits_ ^ > $. В полярных координатах $mathbf < textit > $ представляется как объединение двух треугольников $mathbf < textit > $и $mathbf < textit > $. Уравнение прямой $mathbf < textit > $: $varphi =arctg2$ , прямой $mathbf < textit > $: $varphi =arctg4$, прямой $mathbf < textit > $: $y=24Rightarrow rsin varphi =24Rightarrow quad r=24/sin varphi $, прямой $mathbf < textit > $: $varphi =pi $, прямой $mathbf < textit > $: $y=2x+12Rightarrow rsin varphi =2rcos varphi +12Rightarrow quad r=frac $.

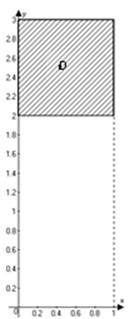
Вычислить двойной интеграл $iintlimits_ < left( 6x < ^ > -12 < ^ > y right)dxdy > $, где область $D$ – квадрат со сторонами $x=0$, $x=1$, $y=2$, $y=3$. В повторном интеграле внутренний интеграл вначале вычислить по переменной $y$, а внешний – по $x$. Вычислить этот же интеграл, изменив порядок интегрирования.

Решение:

Вначале изобразим область интегрирования. Запишем заданный двойной интеграл через повторные: $iintlimits_ < left( 6x < ^ > -12 < ^ > y right)dxdy > =intlimits_ ^ intlimits_ ^ < left( 6x < ^ > -12 < ^ > y right)dy > $.

Внутреннее интегрирование будем выполнять по переменной $y$ , а внешнее – по переменной $x$:

$$=intlimits_ ^ -intlimits_ ^ < 30 < ^ > dx > =38intlimits_ ^ -30intlimits_ ^ < < ^ > dx > =38cdot left. frac < < ^ > > right|_ ^ -30cdot left. frac < < ^ > > right|_ ^ =$$

Вычислим теперь заданный по условию двойной интеграл, сменив порядок интегрирования: внутреннее интегрирование будем проводить по переменной $x$ , а внешнее – по переменной $y$:

$$=intlimits_ ^ < left[ 6 < ^ > intlimits_ ^ -12yintlimits_ ^ < < ^ > dx >right]dy > =intlimits_ ^ < left[ 6 < ^ > cdot left. frac < < ^ > > right|_ ^ -12ycdot left. frac < < ^ > > right|_ ^ right]dy > =$$

$$=intlimits_ ^ < left( 3 < ^ > -4y right)dy > =left. left( 3cdot frac < < ^ > > -4cdot frac < < ^ > > right) right|_ ^ =27-8-2left( 9-4 right)=19-10=9$$

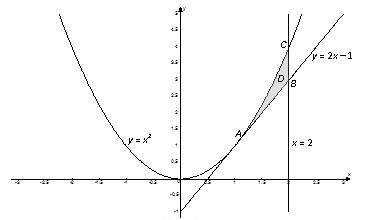
Вычислить двойной интеграл $iintlimits_ < left( < ^ > +2y right)dxdy > $, если область $D$ ограничена линиями $y= < ^ > $, $x=2$, $y=2x-1$. Вычислить этот же интеграл, изменив порядок интегрирования.

Решение:

Строим заданную область $D$. Вначале внутреннее интегрирование будем проводить по переменной $y$, а внешнее – по $x$: $$iintlimits_ < left( < ^ > +2y right)dxdy > =intlimits_ ^ intlimits_ < < _ > left( x right) > ^ < < _ > left( x right) > < left( < ^ > +2y right)dy > $$

Контур области $D$ пересекается любой прямой, параллельной оси ординат, в двух точках.

Найдем пределы интегрирования. Переменная $x$ изменяется от абсциссы точки $A$ к абсциссе точек $B$ и $C$. Координаты точки $A$ найдем как координаты точки пересечения графиков функций $y= < ^ > $ и $y=2x-1$:

$$left[ begin y= < ^ > , \ y=2x-1 \ end right.Rightarrow < ^ > =2x-1Rightarrow < ^ > -2x+1=0Rightarrow < ^ > =0Rightarrow < _ > =1$$

Так как точки $B$ и $C$ лежать на прямой $x=2$, то $ < _ > = < _ > =2$. Итак, $1le xle 2$. Далее на отрезке $left[ 1; 2 right]$ выбираем произвольную точку $x$, через нее проводим прямую, параллельную оси $Oy$, и на этой прямой рассмотрим отрезок $KL$, принадлежащий области $D$.

Область $D$ ограничена снизу прямой $y=2x-1$, а сверху – веткой параболы $y= < ^ > $. Переменная $y$ изменяется в заданной области $D$ от ее значения $2x-1$ на нижней части контура $ABC$ до ее значения $ < ^ > $ на верхней части этого контура.

Замечание. Уравнения линий, ограничивающих контур, должны быть разрешены относительно той переменной, относительно которой находится внутренний интеграл.

Таким образом, $2x-1le yle < ^ > $, а тогда область $D$ задается следующими неравенствами:

$$D:left[ begin 1le xle 2, \ 2x-1le yle < ^ > . \ end right.$$

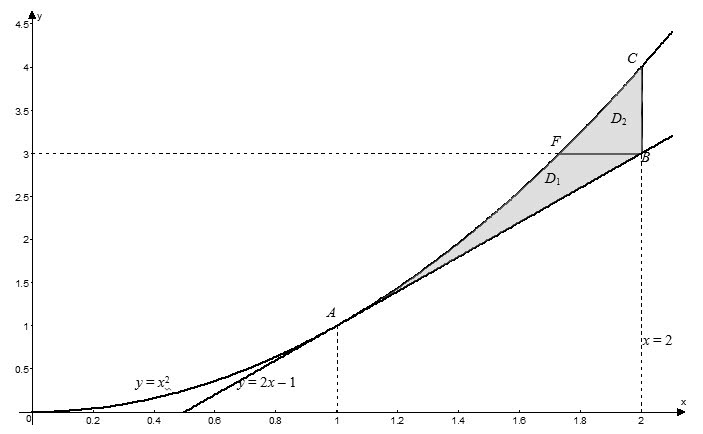
Вычислим теперь рассматриваемый двойной интеграл, изменив порядок интегрирования: внутреннее интегрирование будем проводить по переменной $x$, а внешнее – по $y$. То есть, перейдя к повторным интегралам, получим:

$$iintlimits_ < left( < ^ > +2y right)dxdy > =intlimits_ ^ intlimits_ < < _ > left( y right) > ^ < < _ > left( y right) > < left( < ^ > +2y right)dx > $$ 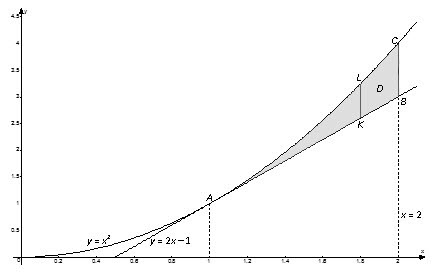Из рисунка в области $D$ видно, что левая граница контура области – одна линия < положительная ветка параболы $y= < ^ > $), а его правая часть состоит из двух линий $AB$ < отрезок прямой $y=2x-1$) и $BC$ < отрезок прямой $x=2$), то есть задается разными уравнениями. В этом случае область $D$ нужно разбить на части так, чтобы каждая из них справа была ограничена только одной линией. В данном случае такими частями будут $ < _ > -ABF$ и $ < _ > -BCF$. Заданная область $D$ будет суммой областей $ < _ > $ и $ < _ > $. Тогда искомый интеграл будет равен сумме интегралов по каждой из областей:

$$iintlimits_ < left( < ^ > +2y right)dxdy > =iintlimits_ < < _ > > < left( < ^ > +2y right)dxdy > +iintlimits_ < < _ > > < left( < ^ > +2y right)dxdy > $$

Поскольку в данном случае внутреннее интегрирование проводится по переменной $x$, то уравнения ограничивающих линий нужно разрешить относительно этой переменной:

$$AB:y=2x-1Rightarrow x=frac ; qquad AC:y= < ^ > Rightarrow x=sqrt $$

Найдем пределы интегрирования для каждой из областей. В области $ < _ > $ переменная $y$ изменяется от ординаты точки $A$ до ординат точек $B$ и $F$. Точка $A$ принадлежит параболе $y= < ^ > $ и выше было найдено, что абсцисса этой точки $ < _ > =1$, тогда $ < _ > = < ^ > =1$. Точка $B$ – точка пересечения двух прямых $x=2$ и $y=2x-1$, а тогда $ < _ > =2cdot 2-1=3$. Итак имеем, что $1le yle 3$. Переменная $x$ в области $ < _ > $ изменяется от ветки параболы $x=sqrt $ до прямой $x=frac $, то есть $ < _ > :left[ begin 1le yle 3, \ sqrt le xle frac . \ end right.$ Аналогично для области $ < _ > $ находим, что $ < _ > :left[ begin 3le yle 4, \ sqrt le xle 2. \ end right.$

Вычислить двойной интеграл (iintlimits_R < left( < + >right)dydx > ,) преобразовав его в полярные координаты. Область интегрирования (R) представляет собой сектор (0 le theta le largefrac normalsize) круга радиусом (r = sqrt 3.)

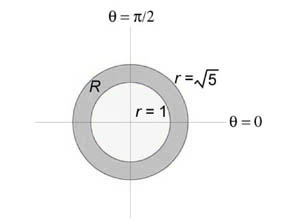
Вычислить интеграл (iintlimits_R ,) в котором область интегрирования (R) представляет собой кольцо, ограниченное окружностями ( + = 1) и ( + = 5.)

Решение:

В полярных координатах область интегрирования (R) является полярным прямоугольником: $R = left( < left( right)|;1 le r le sqrt 5 ,0 le theta le 2pi >right).$

Найти интеграл (iintlimits_R ,) где область интегрирования (R) ограничена кардиоидой (r = 1 + cos theta ).

Решение:

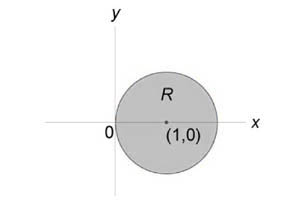
Вычислить интеграл (iintlimits_R < left( < + >right)dxdy > ) в круге ( + = 2x.)

Решение: Область интегрирования (R) показана на рисунке:

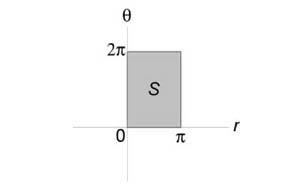
Преобразуем уравнение окружности следующим образом: $ < + = 2x, > ;; < Rightarrow — 2x + 1 + = 1, > ;; < Rightarrow < left( right)^2 > + = 1. > $ Подставляя (x = rcos theta ,) (y = rsin theta ,) найдем уравнение окружности в полярных координатах. $ < + = 2x, > ;; < Rightarrow theta + theta = 2rcos theta , > ;; < Rightarrow left( < < ^2 > theta + theta >right) = 2rcos theta , > ;; $ Образ (S) области интегрирования (R) показан на рисунке:

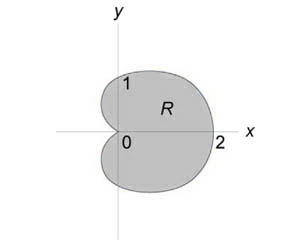
Вычислить двойной интеграл (iintlimits_R < sin sqrt < + > dxdy > ) посредством преобразования в полярные координаты. Область интегрирования (R) представляет собой круг ( + le .)

Решение:

Область интегрирования (R) представлена на рисунке:

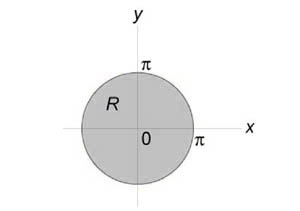
Образ (S) данной области описывается множеством (left[< S = left( right)|;0 le r le pi ,0 le theta le 2pi >right]) и показан на рисунке:

Свойства тройного интеграла

СКНФ. Теорема о представлении в виде СКНФ. Построение СКНФ по таблице

Теорема об аналоге СДНФ в Pk

Вычисление тройного интеграла. Теорема о переходе от тройного интеграла к повторному

Вычисление площади поверхности

Формула Гаусса — Остроградского

Булевы функции от $n$ переменных

Инвариантное определение дивергенции

СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице

Замена переменных в тройном интеграле

Дифференциальные характеристики векторного поля

Критерий полноты

Вычисление двойного интеграла

Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности

Теорема Остроградского

Огравление $Rightarrow $

Видео:Двойные интегралы в полярных координатахСкачать

Презентация к защите

Переход к полярным координатам в двойном интеграле.

Важнейшим частным случаем криволинейных координат являются полярные координаты (r,φ). Они связаны с прямоугольными координатами формулами:, . Якобиан преобразования в этом случае , а формула перехода к полярным координатам в двойном интеграле имеет вид:

(4)

Переходить к полярным координатам удобно в тех случаях, когда область интегрирования есть круг, кольцо или их часть, а так же в случае, когда подынтегральная функция имеет вид . В полярных координатах выражение . Границей круга является окружность и ее уравнение в полярных координатах принимает вид: r=R. Тогда область D — круг в полярной системе координат на плоскости Оrφ переходит в прямоугольную область Ω, которая задается неравенствами : (рис.17а,б).

Интегрирование в полярных координатах проводится по координатным линиям r=const и φ=const. Линии r=const представляют из себя окружности с центром в начале координат. По окружностям происходит изменение координаты φ. Линии φ=const – это семейства лучей, выходящих из начала координат, по которым происходит изменение координаты r. Координатная сетка в полярных координатах изображена на рис.18.