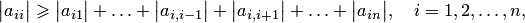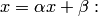Дата добавления: 2014-12-02 ; просмотров: 3137 ; Нарушение авторских прав
1) 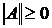
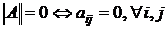
2) 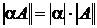
3) 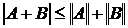
Дополнительно верны следующие свойства:
4) 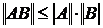
5) 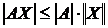
Как и для векторов, для матриц можно определить понятие погрешности.
Определение.Пусть A* – точное значение матрицы, A ‑ приближенное значение. Абсолютная и относительная погрешность матрицы A*: 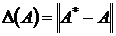 , , 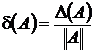 . . |
Пример: Пусть
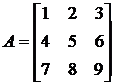
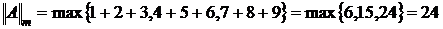
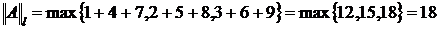
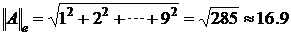
13.)
Метод простых итераций, реализующийся в процессе последовательных приближений, сходится к единственному решению исходной системы 

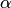
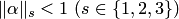
1. Условие теоремы, как достаточное, предъявляет завышенные требования к матрице 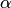
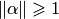
2. Сходящийся процесс обладает свойством «самоисправляемости», т.е. отдельная ошибка в вычислениях не отразится на окончательном результате, так как ошибочное приближение можно рассматривать, как новое начальное.
3. Условия сходимости выполняются, если в матрице 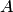
и хотя бы для одного 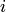
4. Чем меньше величина нормы 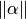
Теорема о необходимом и достаточном условии сходимости метода простых итераций. Для сходимости метода простых итераций (10.12) при любых 
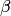
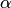
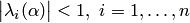
Преобразование системы 
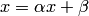
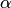
1. Уравнения, входящие в систему 
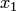
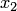
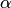
Выражая 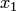
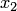
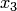
2. Уравнения преобразуются так, чтобы выполнялось условие преобладания диагональных элементов, но при этом коэффициенты 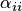
3. Если 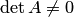

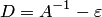
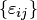
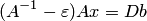
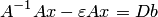
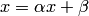
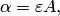
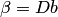
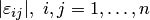
В методе простой итерации если аii 0, то исходная система может быть преобразована к виду хi = bi + aij хj , i j, т.е. из каждого уравнения последовательно выражают хi.
Таким образом, в матричном виде имеем Х = В+ AХ.
Полученную систему будем решать методом последовательных приближений.
За нулевое приближение Х (0) можно принять матрицу В:Х (0) = = B, и далее, подставив найденные значения в исходную систему, получим
Х (1) = В + A Х (0) .
При бесконечном повторении этой вычислительной схемы имеем
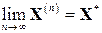
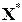
Выбор начального приближения влияет на количество итераций, необходимых для получения приближенного решения. Наиболее часто в качестве начального приближения берут 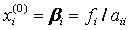
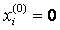
Итерационные методы решения линейных алгебраических систем: (основанны на использовании повторяющегося (циклического) процесса и позволяющие получить решение в результате последовательных приближений.)
Метод Гаусса – Зейделя
Расчетные формулы имеют вид:
т.е. для подсчета i–й компоненты (k+1)–го приближения к искомому вектору используется уже вычисленное на этом, т.е. (k+1)–м шаге, новые значения первых i–1 компонент.
Подробные формулы имеют вид:
Достаточное условие сходимости этого метода такое же, как и для метода простой итерации, т.е. диагональное преобладание:
Видео:Лекция №2.2 НормыСкачать

Сходимость последовательностей
При построении модели явления может возникать задача исследования сходимости последовательностей в линейном нормированном пространстве, например в процессе реализации итерационных алгоритмов. Элементами множества могут быть векторы, матрицы, функции. Сходимость последовательностей векторов и матриц обусловливается наличием предела последовательностей для их одноименных элементов.
В качестве практически важного примера рассмотрим вопросы сходимости на множестве непрерывных функций х(?), определенных
на интервале [я, b.
Последовательность непрерывных функций x^(t), х^ (/), . х^(?) сходится поточечно к функции х(?) на интервале [я, Ь, если в каждой точке t этого интервала для любого сколь угодно малого числа 8 > О существует число K[t, е) такое, что для любого k> K(t, е) выполняется неравенство х^ (?) — х(?)| оо по равномерной норме.
Последовательность х^(?),х^(?), . х^(?). сходится в среднем квадратичном к функции х(?) на [я, Ь, если расстояние между
общим членом последовательности х^(?) и функцией х(?) стремится к нулю при к —> оо по квадратичной норме.
Пример 11.3.1. Рассмотрим на простом примере отличие равномерной нормы от квадратичной нормы при оценке сходимости последовательностей. Пусть задана эмпирическая формула х^ (t) = kt/(l +kt) для аппроксимации разрывной функции х(?) = 1 на интервале [0;1]
(рис. 11.3.1) и задано условие, чтобы k ) = ktj( + kt) и х(?) = 1 по равномерной норме (11.3.1):
Сходимости последовательности к дг(?) по равномерной
норме нет, так как в окрестности точки t = 0 при к —> оо значения эмпирической формулы не входят в ?-окрестность.
Вычислим расстояние по квадратичной норме (11.3.2):
Интегральная оценка расстояния в этом случае пропорциональна площади, заключенной между общим членом последовательности
(?) и функцией x(t>, которая при А:-»оо может стать сколь угодно малой. На рис. 11.3.1 представлена последовательность функций, полученных для значений к = 1,10,100,1000.
Искомое число K[t, s) найдется из неравенства [ . I 99. Число А: = 1000 удовлетворяет погрешности 8 = 0,03.
Видео:Матрицы и векторыСкачать

Матричные ряды
Определение 3.4. Нормой матрицы В = назовем вещественное
число || В || = max Х1&Ч 1
Замечание 3.3. При таком определении нормы матрицы для любого вектора S и любой матрицы В имеем ЦВ^Ц п^+00
В нашем конечномерном случае совершенно очевидно, что это равносильно покомпонентной сходимости:
Говорят, что ряд YjAk сходится к матрице А, если эти частные суммы k=1
Будем рассматривать матричные степенные ряды ? a kA k > А 0 = Е. С каж-
дым матричным рядом связан формальный скалярный комплексный степенной ряд: вместо матрицы А подставим комплексную переменную Z:
и будем обозначать этот ряд /(Z). Нам не важно, сходится он или нет. А матричный ряд будем, соответственно, обозначать /(Л). Через р обозначим радиус сходимости ряда (3.8). Таким образом, 0 z = ? —, р = +оо.
Определение 3.6. Пусть АУВ — (w х /2)-матрицы. Говорят, что матрицы Л и В подобны, А
В, если Л = 5В5 -1 , где S — невырожденная матрица.
Таким образом, все матрицы разбиваются отношением подобия на классы эквивалентности.
В, то ряды /(Л) и f(B) сходятся или расходятся одновременно и в случае сходимости имеет место соотношение /(Л) = = Sf(B)S-K
Доказательство. Рассмотрим частные суммы этих рядов:
x — индукционное предложение.
Теперь видим, что эти суммы сходятся или расходятся одновременно, и в случае сходимости перейдем к пределу. Лемма доказана.
Ряд /(В) сходится тогда и только тогда, когда сходится каждый из рядов f(Bj) для каждого блока отдельно. Более того, в случае сходимости имеет место соотношение
Лемма 3.2. Пусть матрица В имеет квазидиагональный вид:

Доказательство. Заметим, что В к — тоже блочно-диагональная матрица, у которой вдоль главной диагонали будут стоять степени блоков (можно это проверить методом математической индукции). Поэтому akB k =didLg<akBi[. akB k n>. Тогда
и переходим к пределу. Лемма доказана.
По теореме Жордана [1] в каждом классе подобных матриц найдется матрица в жордановой форме. Клетка Жордана имеет вид
Мы выбрали верхнедиагональную форму и обозначили клетку Жордана (жорданову клетку) через А. В частности, если г — 1, то жорданова клетка — это просто число X.
Лемма 3.3. Пусть — клетка Жордана и пусть р —
радиус сходимости степенного ряда /(Z). Тогда:
- 1) если Х р (собственное число за кругом сходимости), то ряд /(А) расходится.
Доказательство. Для доказательства леммы надо просто выписать, чему равно /(А).
Теорема 3.9. Если все собственные числа матрицы А находятся внутри круга сходимости, то f(A) сходится. Если какое-либо собственное число матрицы А лежит вне круга сходимости, то /(А) расходится.
Доказательство. Пусть А — произвольная матрица, Л — ее жорданова форма. Утверждение теоремы следует теперь из лемм 3.1, 3.2, 3.3.
📺 Видео
✓ Критерий Коши сходимости числовых последовательностей | матан #013 | Борис Трушин |Скачать

Занятие 12. Векторы и матрицыСкачать

Собственные значения и собственные векторы матрицы (4)Скачать

Лекция 2, Векторные и матричные нормы, унитарные матрицы, SVDСкачать

Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

А.7.35 Собственные вектора и собственные значения матрицыСкачать

Что такое векторы и матрицы? Душкин объяснитСкачать

Cеминар 11. Равномерная сходимость функциональных последовательностей.Скачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

Собственные векторы и собственные значения матрицыСкачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Айгенвектора и айгензначения | Сущность Линейной Алгебры, глава 10Скачать

Как разложить вектор по базису - bezbotvyСкачать

Линал 2.6. Умножение матрицы на векторСкачать

#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy урокиСкачать

Собственные векторы и собственные числа линейного оператораСкачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

1. Базовые понятия линейной алгебры. Скорости сходимости числовых последовательностей. ФКН 2024Скачать