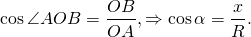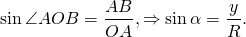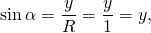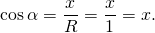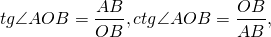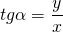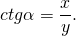Отношение абсциссы к ординате точке единичной окружности это

sin α = y —
ордината точки P_α
cos α = x —
абсцисса точки P_α

1. Определение тригонометрических функций
Через единичную окружность (R = 1)	Через произвольную окружность (R — радиус окружности)	Через прямоугольный треугольник (для острых углов)

tg α = y/x = sin α / cos α

ctg α = x/y = cos α / sin α

2. Тригонометрические функции числового аргумента

sin (числа α) = sin (угла в α радиан)

cos (числа α) = cos (угла в α радиан)

tg (числа α) = tg (угла в α радиан)

ctg (числа α) = ctg (угла в α радиан)

3. Линии тангенсов и котангенсов

tg α = y_A —
ордината соответствующей точки линии тангенсов

СВ — линия котангенсов (СВ || Oх)
ctg α = x_B —
абсцисса соответствующей точки линии котангенсов

Объяснение и обоснование

1. Определение тригонометрических функций. Из курса геометрии вам известно определение тригонометрических функций острого угла в прямоугольном треугольнике. Напомним их.

Синусом острого угла α в прямоугольном треугольнике называется отношение длины противолежащего катета к длине гипотенузы: sin α = a / c (рис. 61).

Косинусом острого угла α в прямоугольном треугольнике называется отношение длины прилежащего катета к длине гипотенузы: cos α = b / c.

Тангенсом острого угла α в прямоугольном треугольнике называется отношение длины противолежащего катета к длине прилежащего: tg α = a / b.

Котангенсом острого угла α в прямоугольном треугольнике называется отношение длины прилежащего катета к длине противолежащего: ctg α = b / a.

В курсе геометрии было обосновано, что синус и косинус острого угла зависят только от величины угла и не зависят от длин сторон треугольника и его расположения, то есть синус и косинус (а таким образом, и тангенс, и котангенс) являются функциями величины угла, которые называются тригонометрическими функциями.

Для сокращения формулировок мы будем использовать термин «тригонометрическая функция угла», понимая, что рассматривается «тригонометрическая функция величины угла» (при этом величина угла может быть выражена как в радианах, так и в градусах).

Также в курсе геометрии с использованием окружности с центром в начале координат было введено определение тригонометрических функций для углов от 0° до 180°. Эти определения можно применить для нахождения тригонометрических функций любых углов. Напомним их (но теперь будем рассматривать любые углы α от –∞ до +∞).

Возьмем окружность радиуса R с центром в начале координат. Обозначим точку окружности на положительной полуоси абсцисс через P₀ (рис. 62). Необходимые нам углы будем образовывать поворотом радиуса OP₀ около точки O. Пусть в результате поворота на угол α около точки O радиус OP₀ займет положение OP_α (говорят, что при повороте на угол α радиус OP₀ переходит в радиус OP_α, а точка P₀ переходит в точку P_α). Напомним, что при α > 0 радиус OP₀ поворачивается против часовой стрелки, а при α * . Удобно взять R = 1, что позволит несколько упростить приведенные определения тригонометрических функций.

* Это следует из того, что две концентрические окружности гомотетичны (центр гомотетии — точка О, а коэффициент гомотетии k — отношение радиусов этих окружностей), тогда и точки Pα на этих окружностях также будут гомотетичны. Таким образом, при переходе от одной окружности к другой в определениях тригонометрических функций числитель и знаменатель соответствующей дроби умножаются на k, а значение дроби не изменяется.

Окружность радиуса 1 с центром в начале координат будем называть единичной окружностью.

Пусть при повороте на угол α точка P₀ (1; 0) переходит в точку P_α (x; y)
(то есть при повороте на угол α радиус OP₀ переходит в радиус OP_α) (рис. 63).

Синусом угла α называется ордината точки P_α (x; y) единичной окружности:

Косинусом угла α называется абсцисса точки P_α (x; y) единичной окружности:

Тангенсом угла α называется отношение ординаты точки P_α (x; y) единичной окружности к ее абсциссе, то есть отношение sin α / cos α.

Таким образом, tg α = sin α / cos α (где cos α ≠ 0).

Заметим, что при cos α = 0 значение функции tg α не определено, а значение функции ctg α не определено при sin α = 0.

Пример

Пользуясь этими определениями, найдем синус, косинус, тангенс и котангенс угла 2π / 3 радиан.

♦ Рассмотрим единичную окружность (рис. 64). При повороте на угол 2π / 3 радиус OP₀ переходит в радиус OP_2π/3 (а точка P₀ переходит в точку P_2π/3). Координаты точки P_2π/3 можно найти, используя свойства прямоугольного треугольника OAP_2π/3 (с углами 60° и 30° и гипотенузой 1): x = — OA=−1/2; y = AP_2π/3 = √3/2. Тогда: sin 2π/3 = y = √3/2; cos 2π/3 = x = -1/2; tg 2π/3 = sin 2π/3 / cos 2π/3 = — √3; ctg 2π/3 = — 1/√3.◊

Аналогично находятся значения синуса, косинуса, тангенса и котангенса углов, градусные и радианные меры которых указаны в верхней строке таблицы 19 (с. 156).

Укажем, что таким образом можно найти тригонометрические функции только некоторых углов. Тригонометрические функции произвольного угла обычно находят с помощью калькулятора или таблиц.

2. Тригонометрические функции числового аргумента. Введенные определения позволяют рассматривать не только тригонометрические функции углов, но и тригонометрические функции числовых аргументов, если рассматривать тригонометрические функции числа α как соответствующие тригонометрические функции угла в α радиан. То есть:

синус числа α — это синус угла в α радиан;
косинус числа α — это косинус угла в α радиан.

Например: sin π/6 = sin (π/6 радиан) = sin 30° = 1/2 (см. также пункт 2 табл. 7).

α	градусы	0 º	30 º	45 º	60 º	90 º	180 º	270 º	360 º
	радианы	0	π/6	π/4	π/3	π/2	π	3π/2	2π
sin α		0	1/2	√2/2	√3/2	1	0	-1	0
cos α		1	√3/2	√2/2	1/2	0	-1	0	1
tg α		0	√3/3	1	√3	—	0	—	0
ctg α		—	√3	1	√3/3	0	—	0	—

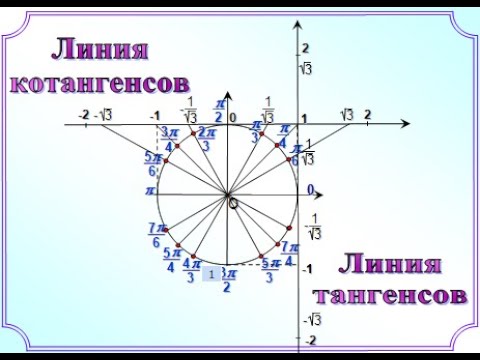
3. Линии тангенсов и котангенсов. Для решения некоторых задач полезно иметь представление о линиях тангенсов и котангенсов.

♦ Проведем через точку P₀ единичной окружности прямую AP₀, параллельную оси Oy (рис. 65). Эта прямая называется линией тангенсов.
Пусть α — произвольное число (или угол), для которого cos α ≠ 0. Тогда точка P_α не лежит на оси Oy и прямая OP_α пересекает линию тангенсов в точке A. Поскольку прямая OP_α проходит через начало координат, то ее уравнение имеет вид y = kx. Но эта прямая проходит через точку P_α с координатами (cos α; sin α), значит, координаты точки P_α удовлетворяют уравнению прямой y = kx, то есть sin α = k cos α. Отсюда k = sin α / cos α = tg α. Следовательно, прямая OP_α имеет уравнение

y = (tg α) x. Прямая AP₀ имеет уравнение x = 1. Чтобы найти ординату точки A, достаточно в уравнение прямой OP_α подставить x = 1. Получаем y_A = tg α. Таким образом,

тангенс угла (числа) α — это ордината соответствующей точки на линии тангенсов.◊

Аналогично вводится и понятие линии котангенсов: это прямая CB (рис. 66), которая проходит через точку C (0; 1) единичной окружности параллельно оси Ox.

Если α — произвольное число (или угол), для которого sin α ≠ 0 (то есть точка P_α не лежит на оси Ox), то прямая OP_α пересекает линию котангенсов в некоторой точке B (x_B; 1).

Аналогично вышеизложенному обосновывается, что x_B = ctg α, таким образом,

котангенс угла (числа) α — это абсцисса соответствующей точки на линии котангенсов.

Вопросы для контроля

1. Сформулируйте определения тригонометрических функций острого угла в прямоугольном треугольнике.

2. Сформулируйте определения тригонометрических функций произвольного угла:
а) используя окружность радиуса R с центром в начале координат;
б) используя единичную окружность.

3. Что имеют в виду, когда говорят о синусе, косинусе, тангенсе и котангенсе числа α?

Упражнения

1°. Постройте на единичной окружности точку Pα, в которую переходит точка P₀ (1; 0) единичной окружности при повороте на угол α. В какой координатной четверти находится точка P_α в заданиях 3–6?
1) α = 3π; 2) α = –4π; 3) α=7π/6;

4) α=−3π/4; 5) α=4π/3; 6) α=7π/4.

2. Найдите значение sin α, cos α, tg α, ctg α (если они существуют) при:
1) α = 3π; 2) α = –4π; 3) α=−π/2;

4) α=5π/2; 5*) α=−5π/6; 6*) α=3π/4.

3°. Пользуясь определением синуса и косинуса, с помощью единичной окружности укажите знаки sin α и cos α, если:
1) α=6π/5; 2) α=−π/6; 3) α=5π/6;

4*. Пользуясь линией тангенсов, укажите знак tg α, если:
1) α=4π/3; 2) α=−3π/4; 3) α=11π/6;

5*. Пользуясь линией котангенсов, укажите знак сtg α, если:
1) α=−4π/3; 2) α=3π/4; 3) α=−11π/6;

Отношение абсциссы к ординате точке единичной окружности это

Введем основные тригонометрические функции.

Пусть радиус-вектор $vec = bar$ точки $M$ образует угол $alpha$ с осью $Ox$ (рис.), причем $x$ и $y$ соответственно абсцисса и ордината конца $M$ вектора, $r$ — его модуль, а величина угла $alpha$ измеряется в градусах или в радианах.

1. Синусом угла $alpha$ (обозначение: $sin alpha$) называется отношение ординаты $y$ (см. рис.) к длине $r$ радиуса-вектора $bar $:

2. Косинусом угла $alpha$ (обозначение: $cos alpha$) называется отношение абсциссы $x$ к длине $r$ радиуса-вектора $bar $:

3. Тангенсом угла $alpha$ (обозначение: $tg alpha$) называется отношение синуса угла $alpha$ к косинусу этого угла:

4. Котангенсом угла $alpha$ (обозначение: $ctg alpha$) называется отношение косинуса угла $alpha$ к синусу этого угла:

5. Секансом угла $alpha$ (обозначение: $sec alpha$) называется величина, обратная $cos alpha$:

6. Косекансом угла $alpha$ (обозначение: $cosec alpha$) называется величина, обратная $sin alpha$:

Замечание 1. Тригонометрические функции (1) — (6) действительно являются функциями только угла $alpha$, т. е. не зависят от длины подвижного радиуса-вектора. Для того чтобы в этом убедиться, достаточно доказать, что если подвижный радиус-вектор $vec$ образует с осью абсцисс данный угол $alpha$, то отношения $frac$ и $frac$ не зависят от длины радиуса-вектора.

Замечание 2. Из определения $tg alpha$ и $ctg alpha$ следует, что

$tg alpha = frac$, (7)
$ctg alpha = frac$. (8)

Соотношения (7) и (8) можно было бы принять в качестве определений для $tg alpha$ и $ctg alpha$.

Замечание 3. Аналогично получаем

$sec alpha = frac$,(9)
$cosec alpha = frac$ (10).

Соотношения (9) и (10) можно было бы также принять в качестве определений для $sec alpha$ и $cosec alpha$.

Замечание 4. Во всех определениях (1) — (6) предполагаем, что соответствующие отношения существуют (имеют смысл). Например, $tg alpha$ имеет смысл, если $cos alpha neq 0, ctg alpha$ имеет смысл, если $sin alpha neq 0$, и т.д. Поскольку (замечание 1) тригонометрические функции (1) — (6) угла $alpha$ не зависят от длины подвижного радиуса-вектора, то в качестве радиуса-вектора можно брать вектор с длиной, равной единице $(| vec| = r = 1)$. Такой вектор называют единичным радиусом-вектором. В случае единичного радиуса-вектора формулы для основных тригонометрических функций запишутся так (рис.):

$begin sin alpha = y, cos alpha = x \ tg alpha = frac, ctg alpha = frac \ sec alpha = frac, cosec alpha = frac end$. (11)

Формулы для $tg alpha$ и $ctg alpha$ остались прежними (см. (7) и (8)), а формулы для остальных основных тригонометрических функций приняли более простой вид (см. (1), (2), (9) и (10)). Следовательно, синус и косинус угла а равны соответственно ординате и абсциссе конца подвижного единичного радиуса-вектора. Конец этого единичного радиуса-вектора при изменении угла а от $0^$ до $360^$ опишет окружность, называемую единичной окружностью (рис.). Для геометрического истолкования тангенса и котангенса вводят понятия оси тангенсов и оси котангенсов. Осью тангенсов называется перпендикуляр, восставленный в точке $A$ к неподвижному радиусу-вектору $bar$. Положительное и отрицательное направления на оси тангенсов выбирают так, чтобы они совпадали с соответствующими направлениями оси ординат (рис.). Рассмотрим угол $alpha = angle AOM$ и введем понятие соответствующей точки оси тангенсов.

а) Если точка $M$ единичной окружности лежит справа от оси ординат, то соответствующей ей точкой оси тангенсов назовем точку $M_$ (точку пересечения продолжения $MO$ с осью тангенсов, рис а.

б) Если точка $M$ единичной окружности лежит слева от оси ординат, то соответствующей ей точкой сси тангенсов назовем точку $M_$ (точку пересечения продолжения $MO$ с ссыо тангенсов, рис. б.

Заметим, что тангенс угла а численно равен ординате $y_$ (рис.) соответствующей точки сси тангенсов, т. е. всегда $tg alpha — y_$. Докажем это для углов первых двух четвертей:

1) $0^ leq alpha < 90^$ (рис. a), $tg alpha = frac<y_> = y_ geq 0$, где $y_$ — ордината точки $M_$.
2) $90^ < alpha leq 180^$ (рис. б). $tg alpha = frac<y_><x_> leq 0$, где $x_$ и $y_$ — абсцисса и ордината точки $M$. Из подобия прямоугольных треугольников $OMM_$ и $OM_A$ имеем

Следовательно, $tg alpha = frac<y_><x_> = y_ leq 0$.

Заметим еще следующее:
а) если точка $M$ лежит на оси ординат (например, $alpha = 270^$), то соответствующей ей точки сси тангенсов не существует, но при этом и $tg alpha$ также не существует;
б) в рассмотренных случаях 1)-2) мы брали угол $alpha$ в пределах от $0^$ до $360^$, но в наших рассуждениях ничего не изменится, если мы будем предполагать угол $alpha$ любым.

Осью котангенсов называется перпендикуляр, восставленный в точке В (конец радиуса-вектора $bar $, образующего с осью $Ox$ угол, равный $90^$) к оси ординат. Положительное и отрицательное направления на оси котангенсов выбирают так, чтобы они совпадали с соответствующими направлениями оси абсцисс (рис.). Введем понятие соответствующей точки оси котангенсов.

а) Если точка $M$ единичной окружности лежит над осью абсцисс, то соответствующей ей точкой оси котангенсов назовем точку $M_$ (точку пересечения продолжения $OM$ с осью котангенсов, рис. а).

б) Если точка $M$ единичной окружности лежит под осью абсцисс, то соответствующей ей точкой сси котангенсов назовем точку (точку пересечения продолжения $MO$ с осью котангенсов, рис. б).

Аналогично предыдущему можно получить, что котангенс угла $alpha$ равен абсциссе $x_$ соответствующей точки оси котангенсов, т. е. $ctg alpha = x_$. Если точка $M$ лежит на оси абсцисс (например, $alpha — 180^$), то соответствующей ей точки оси котангенсов не существует, но при этом и $ctg alpha$ также не существует.

Единичная окружность

Что такое единичная окружность и как с ее помощью вводятся определения синуса, косинуса, тангенса и котангенса?

Рассмотрим в прямоугольной декартовой системе координат окружность с центром в начале координат — точке O.

Отметим на окружности точку P, лежащую на оси абсцисс справа от точки O.

Осуществим поворот радиуса OP около точки O на угол α в верхнюю полуплоскость.

При этом радиус OP займет положение OA. Говорят, что при повороте на угол альфа радиус OP переходит в радиус OA, а точка P переходит в точку точку A(x;y).

Опустив перпендикуляр AB из точки A на ось Оx, получим прямоугольный треугольник OAB, в котором гипотенуза OA равна радиусу окружности, катеты AB и OB — ординате и абсциссе точки A: OA=R, AB=y, OB=x.

Катет AB — противолежащий углу AOB, равному α, катет OB — прилежащий.

По определению косинуса острого угла в прямоугольном треугольнике,

Таким образом, на окружности косинус угла α — это отношение абсциссы точки A окружности к радиусу этой окружности.

Аналогично, по определению синуса острого угла в прямоугольном треугольнике,

Значит, синус угла α — это отношение ординаты точки A окружности к радиусу этой окружности.

Для окружности любого радиуса отношения x/R и y/R не зависят от величины радиуса, а зависят только от угла альфа. Поэтому удобно взять R=1. Для окружности единичного радиуса определение синуса и косинуса упрощаются:

Окружность с центром в начале координат и радиусом, равным единице, называется единичной окружностью.

Отсюда получаем определения синуса и косинуса на единичной окружности.

Синусом угла α называется ордината точки A единичной окружности, полученной при повороте точки P(1;0) на угол α.

Косинусом угла α называется абсцисса точки A единичной окружности, полученной при повороте точки P(1;0) на угол α.

Применив определения тангенса и котангенса острого угла в прямоугольном треугольнике в ∆AOB, получаем:

Приходим к определению тангенса и котангенса на единичной окружности.

Тангенсом угла α называется отношение ординаты точки A единичной окружности к абсциссе этой точки.

Котангенсом угла α называется отношение абсциссы точки A единичной окружности к ординате этой точки.

One Comment

Искала везде. Нигде нет такого подробного и понятного объяснения. Огромное Вам спасибо!

🎦 Видео