Как правильно прочитать треугольник

В математике есть правило: обозначать геометрические фигуры заглавными буквами латинского алфавита. Сегодня мы научимся этому.

Точка

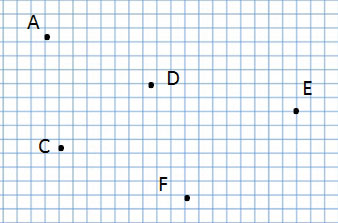
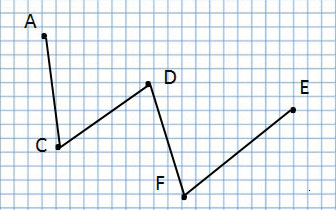
точка А, точка С, точка D, точка Е и точка F.

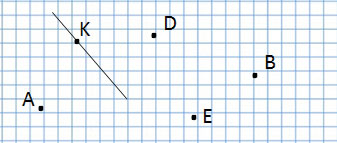
Какая точка лежит на прямой?

Отрезок

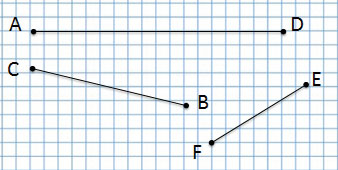
отрезок AD, отрезок СВ, отрезок FE

Сколько всего отрезков на данном чертеже?

Ответ: 6 отрезков.

Ломаная линия

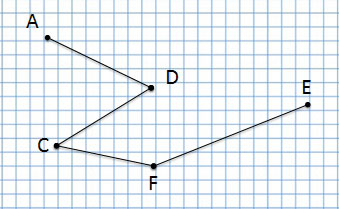
А эта ломаная линия совсем по-другому, потому что соединение точек у неё другое:

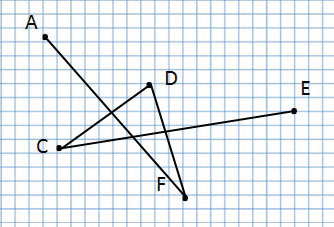
Ломаная линия ACDFE

Прочитаю название следующей ломаной линии:

Ломаная линия AFDCE

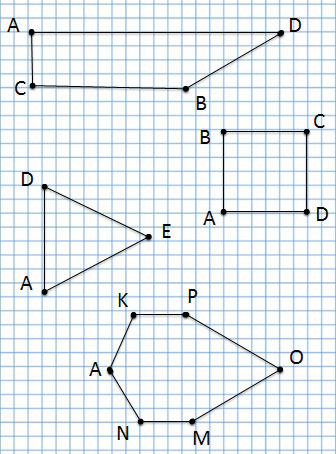
Многоугольники

Угол

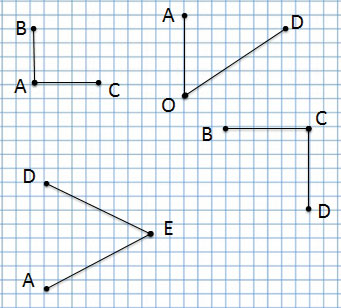
Угол обозначается тремя буквами. В середине указывается буква, которая обозначает вершину угла.

1 угол: угол BAC или CAB с вершиной А

2 угол: угол AOD или DOA с вершиной О

3 угол: угол AED или DEA с вершиной Е

4 угол: угол BCD или DCB с вершиной С

Поделись с друзьями в социальных сетях:

Видео:Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Треугольник

Треугольник — это замкнутая ломаная линия, состоящая из трёх звеньев:

Вершины ломаной называются вершинами треугольника, а её звенья — сторонами треугольника. Углы, образованные двумя сторона треугольника, называются углами треугольника:

В треугольнике ABC вершины A, B и C — это вершины треугольника, звенья AB, BC и CA — стороны треугольника. Три угла — ∠ABC, ∠BCA и ∠CAB — углы треугольника. Часто углы треугольника обозначаются только одной буквой: ∠A, ∠B, ∠C.

Треугольник обычно обозначается тремя буквами, стоящими при его вершинах. Например, треугольник ABC, или BCA, или CBA. Вместо слова треугольник часто используется знак . Так, запись ABC будет читаться: треугольник ABC .

У каждого треугольника 3 вершины, 3 стороны и 3 угла.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Высота

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на его основание. Высота треугольника может быть опущена и на продолжение основания.

Отрезок BN — это высота ABC. Отрезок EL высота DEF, опущенная на продолжение стороны DF.

Длина высоты — это длина отрезка от вершины угла до пересечения с основанием.

Каждый треугольник имеет три высоты.

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Биссектриса

Биссектриса угла треугольника — прямая, делящая угол треугольника пополам. Длина отрезка этой прямой от вершины угла до точки пересечения с противоположной стороной называется длиной биссектрисы.

Отрезок BN — это биссектриса ABC.

Каждый треугольник имеет три биссектрисы.

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Медиана

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Длина этого отрезка называется длиной медианы.

Отрезок BN — это медиана ABC.

Видео:Как найти площадь треугольника без формулы?Скачать

Как называются углы треугольника

Как называются углы треугольника? Ответ может зависеть от того, сколько углов имеется при вершине треугольника.

Если при вершине треугольника есть только один угол, то его можно назвать одной буквой, по названию вершины.

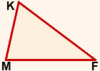
Например, в треугольнике MKF (рисунок 1) при каждой вершине есть только один угол. Следовательно, каждый из углов можно назвать одной буквой, по названию вершины, из которой исходят образующие этот угол лучи:

Угол M, угол K и угол F.

Для обозначения угла существует специальный знак: ∠

Запись ∠ M читают как «угол M».

Каждый из углов треугольника MKF можно назвать также тремя буквами. При этом вершина в названии угла должна стоять посередине.

Угол M также можно назвать углом KMF или углом FMK,

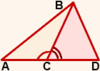
В треугольниках, изображенных на рисунке 2, одной буквой могут быть названы только углы при вершинах A и D: ∠A и ∠D.

При вершине B есть три угла, поэтому каждый из этих углов нужно назвать тремя буквами: ∠ABC, ∠CBD и ∠ABD.

Аналогично, углы при вершине C могут быть названы только тремя буквами: ∠ACB, ∠BCD и ∠ACD. Назвать какой-либо из этих углов ∠C нельзя.

Каждый из углов треугольников, изображенных на рисунке 3, может быть назван только тремя буквами.

🔍 Видео

Как высчитать квадратуру из треугольника,трапеции и т. д.Скачать

Треугольники. 7 класс.Скачать

👉 ФОРМУЛА ГЕРОНА. Площадь треугольника #shortsСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Топография области сосцевидного отростка и треугольника ШипоСкачать

"Композиция в портрете" урок №5 из курса "Лови взгляд!" 2021гСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Сколько треугольников на картинке? Расскажу, как посчитать это за 7 секунд!Скачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Способ сосчитать треугольники, которому не учат в школе! Сколько треугольников на картинке?Скачать

Формулы равностороннего треугольника #shortsСкачать

Технический анализ треугольник [Артём Звёздин]Скачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать