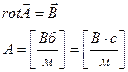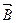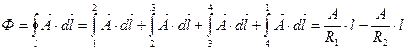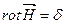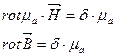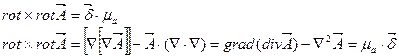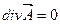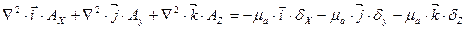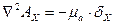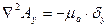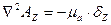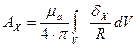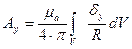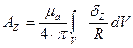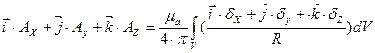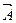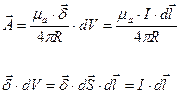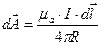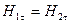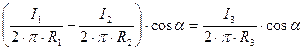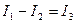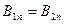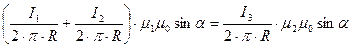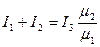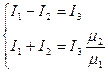Найти вектор потенциал однородного магнитного поля (8 видео)

Векторный потенциал магнитного поля

Векторный потенциал магнитного поля – это плавно меняющаяся от точки к точке векторная величина, ротор которой равен магнитной индукции.

Векторный потенциал можно применять для любых областей пространства, в том числе и для областей занятых токами.

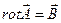
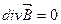
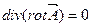
Уравнение возможно с учетом того, что (принцип непрерывности) тогда , а дивергенция от любого ротора равна нулю (из математики).

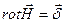
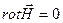
Векторный потенциал магнитного поля вводится для расчета вихревых полей ( ). Но применим и для расчета потенциальных полей .

Направление векторного магнитного потенциала такое же, как и у тока в проводнике.

С помощью векторного потенциала магнитного поля решают следующие типы задач:

1) Определение магнитной индукции

2) Определение магнитного потока, пронизывающего какой-либо контур.

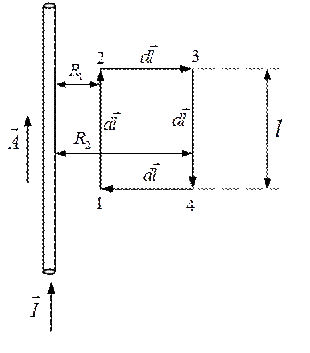
Пример: Определить поток 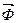, пронизывающий рамку, который создаётся проводником с током.

По теореме Стокса: заменим поверхностный интеграл на линейный (поток через поверхность ограниченную контуром заменим на циркуляцию по контуру):

Уравнение Пуассона

Для областей занятых токами

Умножим обе части уравнения на магнитную проницаемость 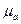=const:

Линии векторного магнитного потенциала замкнуты на себя, то есть:

Тогда 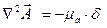-уравнение Пуассона для векторного магнитного потенциала.

Поскольку в обе части уравнения входят векторные величины, то это уравнение можно переписать для декартовой системы координат:

Решая это уравнение, получим проекции на оси координат:

умножим на единичные орты, получим:

— общее решение уравнения Пуассона.

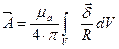
С помощью этой формулы можно найти векторный потенциал в любой точке поля, для этого интеграл в правой части уравнения должен быть взят по всем областям, занятым током.

Однако, пользоваться этой формулой каждый раз нецелесообразно, так как взятие интеграла правой части формулы сопряжено обычно со значительными математическими выкладками.

Пример: В точке А необходимо определить направление

Составляющая векторного магнитного потенциала имеет такое же направление в пространстве, как и ток в элементе проводника.

Метод зеркальных изображений

В магнитном поле постоянного тока, вблизи границы раздела двух сред, для расчета поля используют метод зеркальных изображений.

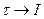
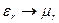
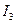
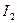
Методика расчета полностью аналогична задаче расчета электростатического поля, созданного двумя заряженными осями, расположенными вблизи плоской границы раздела двух диэлектриков с различными диэлектрическими проницаемостями.. Линейная плотность заряда заменяется током ( ), а относительная диэлектрическая постоянная среды — относительной магнитной постоянной( )

и — фиктивные токи

Найдем фиктивные токи, исходя из граничных условий. Для этого рассмотрим точку, лежащую на границе раздела сред; ее можно считать принадлежащей как к первой, так и ко второй среде.

Из первого граничного условия

Левая часть уравнения определяет принадлежность точки первой среде.

Правая часть уравнения определяет принадлежность точки второй среде.

Сокращая одинаковые элементы в правой и левой частях уравнения, получим

Из второго граничного условия

Левая часть уравнения определяет принадлежность точки к первой среде.

Правая часть уравнения определяет принадлежность точки ко второй среде.

Сокращая одинаковые элементы в правой и левой частях уравнения, получим:

Решая систему из двух уравнений, получим значения фиктивных токов:

Видео:Потенциал электрического поля. 10 класс.Скачать

Векторный потенциал

В этой главе мы продолжим разговор о магнитостатике, т. е. о постоянных магнитных полях и постоянных токах. Магнитное поле и электрические токи связаны нашими основными уравнениями:

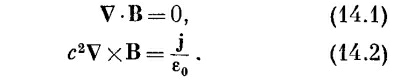Найти вектор потенциал однородного магнитного поля

На этот раз нам нужно решить эти уравнения математически самым общим образом, а не ссылаться на какую-нибудь особую симметрию или на интуицию. В электростатике мы нашли прямой способ вычисления поля, когда известны положения всех электрических зарядов: скалярный потенциал φ дается просто интегралом по зарядам, как в уравнении (4.25) на стр. 77. Если затем нужно знать электрическое поле, то его получают дифференцированием φ. Мы покажем сейчас, что для нахождения поля В существует аналогичная процедура, если известна плотность тока j всех движущихся зарядов.

В электростатике, как мы видели (из-за того, что rot от Е везде равен нулю), всегда можно представить Е в виде градиента от скалярного поля φ. А вот rot от В не везде равен нулю, поэтому представить его в виде градиента, вообще говоря, невозможно. Однако дивергенция В везде равна нулю, а это значит, что мы можем представить В в виде ротора от другого векторного поля. Ибо, как мы видели в гл. 2, § 8, дивергенция ротора всегда равна нулю. Следовательно, мы всегда можем выразить В через поле, которое мы обозначим А:

Или, расписывая компоненты:

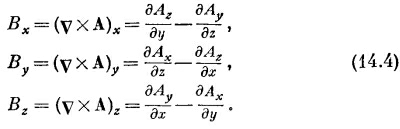Запись В=vхА гарантирует выполнение (14.1), потому что обязательно

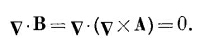Поле А называется векторным потенциалом.

Вспомним, что скалярный потенциал φ оказывается не полностью определенным. Если мы нашли для некоторой задачи потенциал φ, то всегда можно найти столь же хороший другой потенциал φ′, добавив постоянную:

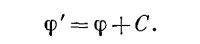Новый потенциал φ′ дает те же электрические поля, потому что градиент vС есть нуль; φ′ и φ отвечают одной и той же картине.

Точно так же у нас может быть несколько векторных потенциалов А, приводящих к одним и тем же магнитным полям. Опять-таки, поскольку В получается из А дифференцированием, то прибавление к А константы не меняет физики дела. Но для А свобода больше. Мы можем добавить к А любое поле, которое есть градиент от некоторого скалярного поля, не меняя при этом физики. Это можно показать следующим образом. Пусть у нас есть А, которое в какой-то реальной задаче дает правильное поле В. Спрашивается, при каких условиях другой векторный потенциал А′, будучи подставлен в (14.3), дает то же самое поле В. Значит, А и А′ имеют одинаковый ротор

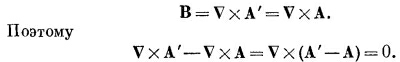Но если ротор вектора есть нуль, то вектор должен быть градиентом некоторого скалярного поля, скажем ψ, так что А′—A=vψ. Это означает, что если А есть векторный потенциал, отвечающий данной задаче, то при любом ψ

также будет векторным потенциалом, в одинаковой степени удовлетворяющим данной задаче и приводящим к тому же полю В.

Обычно бывает удобно уменьшить «свободу» А, накладывая на него произвольно некоторое другое условие (почти таким же образом мы считали удобным — довольно часто — выбирать потенциал φ равным нулю на больших расстояниях). Мы можем, например, ограничить А, наложив на него такое условие, чтобы дивергенция А чему-нибудь равнялась. Мы всегда можем это сделать, не задевая В. Так получается потому, что, хотя А′ и А имеют одинаковый ротор и дают одно и то же В, они вовсе не обязаны иметь одинаковую дивергенцию. В самом деле, v·A` = v·A+ v 2 ψ, и, подбирая соответствующее ψ, можно придать v·A′ любое значение.

Чему следует приравнять v·А? Выбор должен обеспечить наибольшее математическое удобство и зависит от нашей задачи. Для магнитостатики мы сделаем простой выбор

(Потом, когда мы перейдем к электродинамике, мы изменим наш выбор.) Итак, наше полное определение А в данный момент есть vхА = В и v·А = 0.

Чтобы привыкнуть к векторному потенциалу, посмотрим сначала, чему он равен для однородного магнитного поля В₀. Выбирая ось z в направлении В₀, мы должны иметь

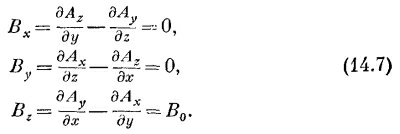Рассматривая эти уравнения, мы видим, что одно из возможных решений есть

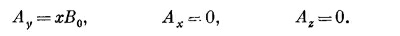Или с тем же успехом можно взять

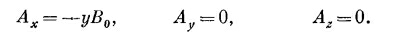Еще одно решение есть комбинация первых двух

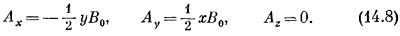Ясно, что для каждого поля В векторный потенциал А не единственный; существует много возможностей.

Третье решение [уравнение (14.8)] обладает рядом интересных свойств. Поскольку х-компонента пропорциональна –у, а y-компонента пропорциональна +х, то вектор А должен быть перпендикулярен вектору, проведенному от оси z, который мы обозначим r′ (штрих означает, что это не вектор расстояния от начала). Кроме того, величина А пропорциональна √x 2 + y 2 и, следовательно, пропорциональна r`. Поэтому А (для однородного поля) может быть записано просто

Векторный потенциал А равен по величине Вr′/2 и вращается вокруг оси z, как показано на фиг. 14.1. Если, например, поле В есть поле внутри соленоида вдоль его оси, то векторный потенциал циркулирует точно таким же образом, как и токи в соленоиде.

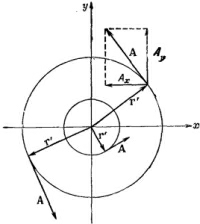
Векторный потенциал однородного поля может быть получен и другим способом. Циркуляция А вдоль любой замкнутой петли Г может быть выражена через поверхностный интеграл от vХА с помощью теоремы Стокса [уравнение (3.38), стр. 63]

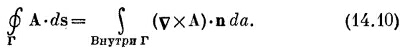Но интеграл справа равен потоку В сквозь петлю, поэтому

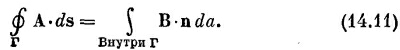Итак, циркуляция А вдоль всякой петли равна потоку В сквозь петлю. Если мы возьмем круглую петлю радиуса r′ в плоскости, перпендикулярной однородному полю В, то поток будет в точности равен

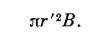Если выбрать начало отсчета в центре петли, так что А можно считать направленным по касательной и функцией только от r′, то циркуляция будет равна

Видео:Физика - Магнитное полеСкачать

Векторный потенциал магнитного поля

Вектор магнитной индукции можно представить в виде вихря некоторого вспомогательного вектора А:

причем вектор А при заданном распределении в пространстве электрических токов является функцией координат.

Вектор А называется векторным потенциалом магнитного поля. Определим его так, чтобы уравнения магнитного поля

выполнялись во всем пространстве — и там, где отсутствуют токи, и там, где они есть , т.е. J ^ 0.

Подчиним вектор А условию div А = 0, т.е. будем считать, что поле вектора А не имеет источников.

Установим связь между магнитным потоком Ф сквозь некоторую поверхность s и векторным потенциалом А магнитного поля. Имеем

Согласно теореме Стокса Jrot Ads = 2 ф = -—. Решение этого уравнения

Отсюда запишем проекции вектора А:

Зная проекции, определим вектор

Для нахождения магнитного поля линейного тока рассмотрим рис. 3.4. Пусть известна плотность линейного тока J. Тогда

Рис. ЗА. Определение вектора магнитного потенциала для линейного тока

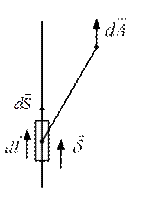
Поскольку ток I = J JdS,

Определим подынтегральное выражение. Пусть a=dl, 2

Подставив полученные результаты в уравнение (3.6), получаем

Это интегральная формулировка так называемого закона Био и Савара, непосредственно связывающего напряженность магнитного поля с линейным распределением тока.

В дифференциальной форме этот закон имеет вид