Вокруг тупоугольного треугольника нельзя описать окружность

Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов

Серединный перпендикуляр к отрезку

Окружность описанная около треугольника

Свойства описанной около треугольника окружности. Теорема синусов

Доказательства теорем о свойствах описанной около треугольника окружности

Серединный перпендикуляр к отрезку

Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.

Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.

Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .

Докажем, что отрезок AE длиннее отрезка EB . Действительно,

Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,

Полученное противоречие и завершает доказательство теоремы 2

Окружность, описанная около треугольника

Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .

Свойства описанной около треугольника окружности. Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

,

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Фигура	Рисунок	Свойство
Серединные перпендикуляры к сторонам треугольника		Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство
Окружность, описанная около треугольника		Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство
Центр описанной около остроугольного треугольника окружности		Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружности		Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство
Центр описанной около тупоугольного треугольника окружности		Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теорема синусов
Площадь треугольника
Радиус описанной окружности

Серединные перпендикуляры к сторонам треугольника

Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Окружность, описанная около треугольника

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Центр описанной около остроугольного треугольника окружности

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центр описанной около прямоугольного треугольника окружности

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.

Центр описанной около тупоугольного треугольника окружности

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

,

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Площадь треугольника

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Радиус описанной окружности

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Доказательства теорем о свойствах описанной около треугольника окружности

Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).

Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:

Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:

Следовательно, справедливо равенство:

откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.

Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).

При доказательстве теоремы 3 было получено равенство:

из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.

Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)

.

Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:

l = 2Rsin φ .

(1)

Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).

Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.

Формула (1) доказана.

Из формулы (1) для вписанного треугольника ABC получаем (рис.7):

Окружность, описанная около треугольника

Определение окружности, описанной около треугольника

Определение 1. Окружностью, описанной около треугольника называется окружность, проходящей через все три вершины треугольника (Рис.1).

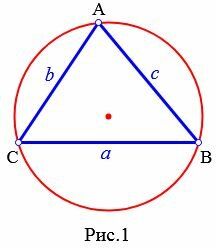При этом треугольник называется треугольником вписанным в окружность .

Теорема об окружности, описанной около треугольника

Теорема 1. Около любого треугольника можно описать окружность.

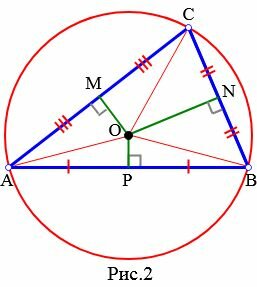Доказательство. Пусть задан произвольный треугольник ABC (Рис.2). Обозначим точкой O точку пересечения серединных перпендикуляров к его сторонам. Проведем отрезки OA, OB и OC. Поскольку точка O равноудалена от точек A, B и C, то OA=OB=OC. Тогда окружность с центром O и радиусом OA проходит через все три вершины треугольника ABC и, следовательно, является окружностью, описанной около треугольника ABC.

Из теоремы 1 следует, что центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника.

Замечание 1. Около любого треугольника можно описать только одну окружность.

Доказательство. Допустим, что около треугольника можно описать две окружности. Тогда центр каждой из этих окружностей равноудален от вершин треугольника и совпадает с точкой O пересечения серединных перпендикуляров сторон треугольника. Радиус этих окружностей равен расстоянию от точки O до вершин треугольника. Поэтому эти окружности совпадают.

Задание 13 ГИА по теме «Треугольники»
материал для подготовки к егэ (гиа) по геометрии (9 класс) на тему

В работе представлены 30 заданий «верно-неверно», прототипов к Заданию 13 ГИА.

Скачать:

Вложение	Размер
zadacha_13verno-neverno.doc	27.5 КБ

Предварительный просмотр:

Укажите в ответе номера верных утверждений:

1. Треугольники, имеющие равные площади, равны.
2. Точка пересечения медиан треугольника является центром описанной окружности треугольника.
3. Треугольники, имеющие одно основание, а вершины, находящиеся на прямой, параллельной основанию треугольника, равновелики.
4. Если в равнобедренном треугольнике угол при вершине острый, то такой треугольник — остроугольный.
5. Отношение стороны треугольника к синусу противоположного угла равно диаметру окружности, вписанной в треугольник.
6. Во всяком треугольнике высота, проведенная к основанию, совпадает с медианой.
7. В прямоугольном треугольнике тангенсом острого угла называется отношение .
8. Во всяком треугольнике биссектриса угла равна его медиане.
9. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники равны.
10. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
11. Около любого треугольника можно описать окружность.
12. В равностороннем треугольнике ABC медиана AK равна высоте CH.
13. Внешний угол треугольника всегда тупой.
14. Сумма катетов прямоугольного треугольника больше его гипотенузы.
15. Медиана, проведенная из вершины прямого угла, равна половине гипотенузы.
16. Площадь прямоугольного треугольника равна произведению двух его катетов.
17. Если в равнобедренном треугольнике один из углов равен , то такой треугольник – правильный.
18. В любом треугольнике против большего угла лежит большая сторона.
19. Если любая сторона первого треугольника больше любой стороны второго треугольника, то площадь первого треугольника больше площади второго треугольника.
20. Гипотенуза – самая длинная сторона в прямоугольном треугольнике.
21. Один из катетов может быть в три раза короче другого.
22. Вокруг тупоугольного треугольника нельзя описать окружность.
23. Сумма углов в тупоугольном треугольнике больше, чем в остроугольном.
24. Медианы треугольника пересекаются в одной точке.
25. Если медиана треугольника является его высотой, то этот треугольник равнобедренный.
26. Высота прямоугольного треугольника, опущенная на гипотенузу, делит его на два подобных треугольника.
27. Если два угла одного треугольника пропорциональны двум углам другого треугольника, то такие треугольники подобны.
28. Треугольник с углами существует.
29. Сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы.
30. Радиус окружности, описанной около правильного треугольника, равняется двум третьим его высоты.

Верные утверждения: 3, 4, 7, 10, 11, 12, 14, 15, 17, 18, 19, 20, 21, 25, 29, 30.

По теме: методические разработки, презентации и конспекты

Домашнее задание — это очень важное задание!

Совет для родителей.

Математика 6 класс. «Координатная плоскость» Задания для развития и обучения учащихся (задания для интерактивной доски)

Задания для развития и обучения учащихся. Задания для интерактивной доски. Данный материал можно использовать для закрепления или повторения темы.

Задания к стартовой контрольной работе по географии в 7 кл., Задания промежуточной аттестации по географии в 7 кл.(переводной экзамен).

Задания к стартовой контрольной работе по географии в 7 кл., Задания промежуточной аттестации по географии в 7 кл.(переводной экзамен). .

Структура задания и презентация компетентностно-ориентированного задания

Презентация «Метапредметные результаты. Компетентностно-ориентированные задания. » Структура задания. Материал предназначен для урока биологии в 7 классе.

Практические работы, творческие задания, викторины, контрольные задания, тестовые задания для занятий в объединении «КОМП»

Практические работы, творческие задания, викторины, контрольные задания, тестовые задания для проверки навыков работы в старндартных прогаммах.

задание для подготовки ОГЭ по информатике (задание по Exel, задание 19)

Данный фал может использоваться как для подготовки, так и для итоговой проверки по 19 заданию ОГЭ по информатике. На закладках файла собраны тексты и сами задания для школьников.

Работа состоит из 3-х частей. Часть А – задания с выбором 1 ответа, каждый ответ оценивается в 1 балл. Часть В — задания на установления соответствия оценивается в 2 балла. Часть С – задания с развернутым ответом, оценивается в 3 балла. Максимальное кол

Работа состоит из 3-х частей. Часть А – задания с выбором 1 ответа, каждый ответ оценивается в 1 балл. Часть В — задания на установления соответствия оценивается в 2 балла. Часть С .

🌟 Видео