Найти площадь параллелограмма если известны координаты векторов

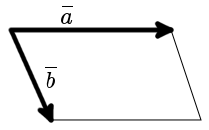
Этот онлайн калькулятор позволит вам очень просто найти площадь параллелограмма построенного на векторах.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление площади параллелограмма построенного на векторах и закрепить пройденый материал.

Видео:Площадь параллелограмма, построенного на данных векторахСкачать

Калькулятор для вычисления площади параллелограмма построенного на векторах

Выберите каким образом задается параллелограмм:

Введите значения векторов: Введите координаты трех любых вершин параллелограмма:

Инструкция использования калькулятора для вычисления площади параллелограмма построенного на векторах

Ввод данных в калькулятор для вычисления площади параллелограмма построенного на векторах

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора вычисления площади параллелограмма построенного на векторах

• Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Видео:Площадь параллелограмма по векторамСкачать

Теория. Площадь параллелограмма построенного на векторах.

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Найдите площадь параллелограмма, построенного на векторахСкачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Как найти площадь параллелограмма?Скачать

Калькулятор онлайн.
Вычисление площади параллелограмма построенного на векторах.

Этот калькулятор онлайн вычисляет площадь параллелограмма построенного на векторах. Параллелограмм может быть задан координатами двух векторов или координатами трех вершин.

Онлайн калькулятор для вычисления площади параллелограмма построенного на векторах не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac )

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac )

Видео:8 класс, 13 урок, Площадь параллелограммаСкачать

Найти площадь параллелограмма,построенного на векторах!=(

векторы: (a+3b) и (3a+b), если |a|=|b|=1, а угол между векторами а и b равен 30 градусов.

Площадь параллелограмма, построенного на векторах, вычисляется как произведение длин этих векторов на синус угла между ними. Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между ))))))))))))
1
В том случае, если известны длины векторов и угол между ними, то для того, чтобы найти площадь параллелограмма, построенного на векторах, найдите произведение их модулей (длин векторов) , на синус угла между ними S=│a│•│ b│•sin(α).
2
Если векторы заданы в декартовой системе координат, то для того, чтобы найти площадь параллелограмма, построенного на них, проделайте следующие действия:
3
Найдите координаты векторов, если они не даны сразу, отняв от соответствующих координат концов векторов, координаты из начал. Например, если координаты начальной точки вектора (1;-3;2), а конечной (2;-4;-5), то координаты вектора будут (2-1;-4+3;-5-2)=(1;-1;-7). Пусть координаты вектора а (x1;y1;z1), вектора b(x2;y2;z2).
4
Найдите длины каждого из векторов. Возведите каждую из координат векторов в квадрат, найдите их сумму x1²+y1²+z1². Из получившегося результата извлеките корень квадратный. Для второго вектора проделайте ту же процедуру. Таким образом, получится │a│и│ b│.
5
Найдите скалярное произведение векторов. Для этого перемножьте их соответствующие координаты и сложите произведения │a b│= x1• x2+ y1•y2+ z1• z2.
6
Определите косинус угла между ними для чего скалярное произведение векторов, получившееся в п. 3 поделите на произведение длин векторов, которые были рассчитаны в п. 2 (Cos(α)= │a b│/(│a│•│ b│)).
7
Синус полученного угла будет равен корню квадратному из разности числа 1, и квадрата косинуса того же угла, рассчитанного в п. 4 (1-Cos²(α)).
8
Рассчитайте площадь параллелограмма, построенного на векторах найдя произведение их длин, вычисленное в п. 2, а результат умножьте на число, получившееся после расчетов в п. 5.
9
В том случае, если координаты векторов заданны на плоскости, при расчетах координата z просто отбрасывается. Данный расчет является числовым выражением векторного произведения двух векторов.

Найти площадь параллелограмма построенного на векторах с координатами (2,-2, 0, 1, 2) и (-1, 0, 2, 2, -2)

📸 Видео

№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

как найти площадь параллелограмма построенного на векторахСкачать

Площадь треугольника, построенного на векторахСкачать

Задача 4. Вычислить площадь параллелограмма, построенного на векторах.Скачать

18 ЗАДАНИЕ ОГЭ НАЙТИ ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММАСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

§16 Нахождение площади параллелограммаСкачать

8 класс. Площадь параллелограмма. Геометрия.Скачать

Найти угол между векторами и площадь параллелограмма, построенного на этих векторахСкачать

1. Векторы и параллелограмм задачи №1Скачать

Координаты вектора. 9 класс.Скачать

Геометрия 8 класс (Урок№9 - Площадь параллелограмма.)Скачать

Найдите вершину A параллелограмма ABCD, если B(3; −4; 7), C(−5; 3; −2) и D(1; 2; −3)Скачать

Геометрия 8 класс. Площадь параллелограммаСкачать