Прямая ке касается окружности с центром

Видео:Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Прямая КЕ касается окружности с центром в точке О, К — точка касания, найдите ОЕ если КЕ — 8см, а радиус окружности 7см?

Геометрия | 5 — 9 классы

Прямая КЕ касается окружности с центром в точке О, К — точка касания, найдите ОЕ если КЕ — 8см, а радиус окружности 7см.

Радиус перпендикулярен касательной, т.

О. получаем прямоугольный тряугольник OKE с углом K = 90 градусов.

ДАлее по теореме пифагора

OE ^ 2 = 8 ^ 2 + 7 ^ 2

Видео:Урок 3. №23 ОГЭ. Касательная. Окружность с центром на стороне AC касается АВ в точке В.Скачать

Две окружности с центрами в точках о и о1 и радиусами 5 и 3 соответственно касаются сторон угла А(В и В1 — точки касания)?

Две окружности с центрами в точках о и о1 и радиусами 5 и 3 соответственно касаются сторон угла А(В и В1 — точки касания).

Найдите расстояние между центрами окружностей, если АВ1 = 4.

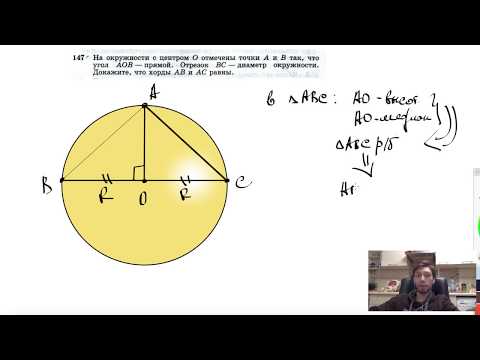
Видео:№147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВССкачать

Прямая MN касается окружности с центром в точке О, М — точка касания, угол МNO = 30 градусов а радиус окружности равен 5 см найдите NO?

Прямая MN касается окружности с центром в точке О, М — точка касания, угол МNO = 30 градусов а радиус окружности равен 5 см найдите NO.

Видео:На окружности с центром O отмечены точки A и B так ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Прямая АВ касается окружности с центром в точке О и радиусом 15 см в точке В?

Прямая АВ касается окружности с центром в точке О и радиусом 15 см в точке В.

Найдите АВ, если АО = 17 см.

Видео:В окружности с центром O AC и BD – диаметры ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Прямая КЕ касается окружности с центром в точке О, К — точка касания?

Прямая КЕ касается окружности с центром в точке О, К — точка касания.

Найдите ОЕ если КЕ = 8 см.

А радиус окружности равен 6 см.

Видео:Отрезки AC и BD – диаметры окружности с центром O ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Прямая АВ касается окружности с центром в точке О и радиусом равном 9 см в точке В?

Прямая АВ касается окружности с центром в точке О и радиусом равном 9 см в точке В.

Найдите АВ, если АО = 41 см.

Видео:2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать

Прямая AB касается окружности с центром о и радиусом 15 см в точке В?

Прямая AB касается окружности с центром о и радиусом 15 см в точке В.

Найдите АВ, если ОА = 17 см.

Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Прямая АВ касается окружности с центром в точке О и радиусом, равным 9 см, в точке В Найдите АВ, если АО = 41 см?

Прямая АВ касается окружности с центром в точке О и радиусом, равным 9 см, в точке В Найдите АВ, если АО = 41 см.

Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Прямая АВ касается окружности с центром в точке О и радиусом, равным 7 см, в точке А?

Прямая АВ касается окружности с центром в точке О и радиусом, равным 7 см, в точке А.

Найдите ОВ, если АВ = 24 см.

Видео:Через точку A, лежащую вне окружности, проведены две прямые.Скачать

Прямая DC касается окружности(С — точка касания)?

Прямая DC касается окружности(С — точка касания).

Найдите радиус окружности, если DO = 6 см, DC = 5 см.

Видео:Найти центр и радиус окружностиСкачать

Помогите СРОЧНО Дана окружность радиуса 3 см и точка А на расстоянии, равном 5 см от центра окружности?

Помогите СРОЧНО Дана окружность радиуса 3 см и точка А на расстоянии, равном 5 см от центра окружности.

Найдите радиус окружности, касающейся данной и имеющей центр в точке А.

Перед вами страница с вопросом Прямая КЕ касается окружности с центром в точке О, К — точка касания, найдите ОЕ если КЕ — 8см, а радиус окружности 7см?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

10 кг = 13. 4 к. е. Тогда 1кг = 1. 34 к. Е. (отношение к. Ек кг = 1. 34) 23. 5 центнеров = 23500 кг 23500×1. 34 = 31490 (к. Е) 31490 к. Е. = 31. 49 центнеров к. Е. Ответ : 31. 49ц.

Отрезок CD называется суммой отрезков CE и ED, если все три точки лежат на одной прямой, при этом точка E находится между точками C и D.

8 + 16 + 17 = 41 если я не ошибаюсь то так . Наверно.

Боковые ребра пирамиды равны, значит вершина пирамиды проецируется в центр основания (пересечение диагоналей прямоугольника). Грани пирамиды — по два равнобедренных треугольника с основаниями 16 см и 12 см и высотами√(26² — 8²) = 6√17см и√(26² — 6²)..

Собственно, решений много, тут можно построить график x = — 2y 1 точка x = 0 ; y = 0 2 точка x = 2 ; y = — 1 3 точка x = 4 ; y = — 2 Т. Е. это будет прямая, находящаяся в 1 и 3 четверти.

Много решений, одно из них : x = 0 y = 2 0 + 2×0 = 0 Также просто x = — 2 y = 1 ответ 0 получается вот и всё).

Если периметр ромба 32, то каждая сторона, это 32 / 4 = 8 (т. К. У ромба 4 стороны). Формула площади : сторона в квадрате и на синус угла между двумя сторонами : s = a ^ 2 * Sina = 8 * 8 * 1 / 2 = 32.

Найдём высоту цилиндра H = 64π / 16π = 4 см Найдём радиус основания цилиндра R = 16π / 2π = 8 см Найдём площадь основания цилиндра S = πR² S = 64π см² Найдём объём цилиндра V = SH V = 64π * 4 = 256π см³ Ответ объём цилиндра256π см³.

Цилиндр — D — 6√2 D = a + a = 2 * a = D = a√2 = a = 6 S = Sбок≠2πRh, R≈a / 2, h = a ⇒ S≠2πa * a / 2≠πa², S = 36π≈113, 04(боковая поверхность) V = πR²h≠πa³ / 4 = V≠54π≈169, 56(объём цилиндра).

Площадь сечения 3, 456 ну а высота самой перамиды 12√3. 64m×12÷2 и ×на 576.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Касательная к окружности

О чем эта статья:

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°

📺 Видео

№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

№146. Отрезки АВ и CD — диаметры окружности с центром О. Найдите периметр треугольника AOD, еслиСкачать

Демо-вариант ОГЭ. Задача 26Скачать

ЕГЭ задание 16 Внутреннее касание двух окружностейСкачать