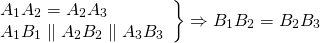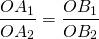Доказательство теоремы фалеса в треугольнике (5 видео)

Теорема Фалеса. Доказательство

Теорема 1 (Теорема Фалеса) . Пусть через точки ( small A, B, C, D ) расположенные на одной стороне угла проведены параллельные прямые, которые пересекают другую сторону этого угла в точках ( small A_1, B_1, C_1, D_1, ) соответственно. Тогда если равны отрезки ( small AB ) и ( small CD, ) то равны и отрезки ( small A_1B_1 ) и ( small C_1D_1. )

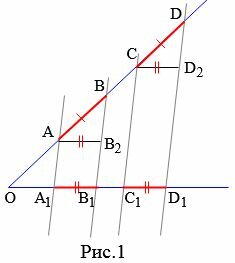Доказательство теоремы фалеса в треугольнике

Доказательство. Пусть ( small AB=CD ) и пусть прямые ( small AA_1, BB_1, CC_1, DD_1 ) параллельны (Рис.1). Докажем, что ( small A_1B_1=C_1D_1. ) Проведем прямые ( small AB_2 ) и ( small CD_2 ) параллельно стороне ( small OD_1. ) Получили два четырехугольника ( small AB_2B_1A_1 ) и ( small CD_2D_1C_1. ) Эти четырехугольники являются параллелограммами поскольку противоположные стороны этих четырехугольников параллельны. Тогда

( small AB_2=A_1B_1, ) ( small CD_2=C_1D_1. )

(1)

Углы ( small BAB_2 ) и ( small DCD_2 ) являются соответствующими углами при пересечении параллельных прямых ( small AB_2 ) и ( small CD_2 ) секущей ( small AD ) (см. статью Теоремы об углах, образованных двумя параллельными прямыми и секущей). Тогда

( small &angle;BAB_2=&angle;DCD_2. )

(2)

Углы ( small ABB_2 ) и ( small CDD_2 ) являются соответствующими углами при пересечении параллельных прямых ( small BB_2 ) и ( small DD_2 ) секущей ( small AD. ) Тогда

( small &angle;ABB_2=&angle;CDD_2. )

(3)

Треугольники ( small ABB_2 ) и ( small CDD_2 ) равны по второму признаку равенства треугольников так как ( small AB=CD ) и выполнены равенства (2) и (3). Следовательно ( small AB_2 = CD_2. ) Отсюда, учитывая (1) получим: ( small A_1B_1=C_1D_1. ) Теорема доказана.

Содержание

Теорема Фалеса: формулировка и пример решения задачи
Формулировка теоремы
Обобщенная формулировка
Обратная теорема Фалеса
Пример задачи
Теорема Фалеса
📸 Видео

Видео:Геометрия 8. Урок 8 - Теорема Фалеса - теорияСкачать

Теорема Фалеса: формулировка и пример решения задачи

В данной публикации мы рассмотрим одну из основных теорем по геометрии 8 класса – теорему Фалеса, которая получила такое название в честь греческого математика и философа Фалеса Милетского. Также разберем пример решения задачи для закрепления изложенного материала.

Видео:Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать

Формулировка теоремы

Если на одной из двух прямых отмерить равные отрезки и через их концы провести параллельные прямые, то пересекая вторую прямую они отсекут на ней равные между собой отрезки.

Примечание: Взаимное пересечение секущих не играет роли, т.е. теорема верна и для пересекающихся прямых, и для параллельных. Расположение отрезков на секущих, также, не важно.

Обобщенная формулировка

Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках*: параллельные прямые отсекают на секущих пропорциональные отрезки.

В соответствии с этим для нашего чертежа выше справедливо следующее равенство:

* т.к. равные отрезки, в т.ч., являются пропорциональными с коэффициентом пропорциональности, равным единице.

Обратная теорема Фалеса

1. Для пересекающихся секущих

Если прямые пересекают две другие прямые (параллельные или нет) и отсекают на них равные или пропорциональные отрезки, начиная от вершины, значит эти прямые являются параллельными.

Из обратной теоремы следует:

Обязательное условие: равные отрезки должны начинаться от вершины.

2. Для параллельных секущих

Отрезки на обеих секущих должны быть равны между собой. Только в этом случае теорема применима.

Видео:ТЕОРЕМА ФАЛЕСА доказательство 384 Атанасян 8 классСкачать

Пример задачи

Дан отрезок AB на плоскости. Разделите его на 3 равные части.

Решение

Проведем из точки A прямую a и отметим на ней три подряд идущих равных отрезка: AC, CD и DE.

Крайнюю точку E на прямой a соединяем с точкой B на отрезке. После этого через оставшиеся точки C и D параллельно BE проведем две прямые, пересекающие отрезок AB.

Образованные таким образом точки пересечения на отрезке AB делят его на три части, равные между собой (согласно теореме Фалеса).

Видео:Теорема Фалеса. 8 класс.Скачать

Теорема Фалеса

Теорема Фалеса может быть сформулирована не только для угла, но и для прямых. Кроме того, существует еще и обобщенная теорема Фалеса.

Если параллельные прямые отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Теорема Фалеса может быть сформулирована не только для угла, но и для прямых.

Если параллельные прямые пересекают две данные прямые и отсекают на одной прямой равные отрезки, то они отсекают равные отрезки и на другой прямой.

Теорема о пропорциональных отрезках (обобщенная теорема Фалеса).

Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

Теорема Фалеса и ее модификации применяется в том числе, и в задачах на построение (в частности, для деления отрезка на n равных частей и при построении четвертого пропорционального отрезка).