| Фигура | Рисунок | Формулировка | ||||||||||||||||||||||||||||
| Прямоугольный треугольник | ||||||||||||||||||||||||||||||
| Равнобедренный прямоугольный треугольник | ||||||||||||||||||||||||||||||
| Прямоугольный треугольник с углом в 30° |
| Прямоугольный треугольник | ||||||||||||||||||||
| Равнобедренный прямоугольный треугольник | ||||||||||||||||||||
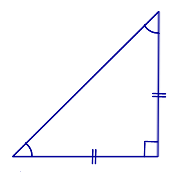 Определение равнобедренного прямоугольного треугольника: Равнобедренным прямоугольным треугольником называют такой прямоугольный треугольник, у которого равны катеты. Свойство углов прямоугольного треугольника: Острые углы равнобедренного прямоугольного треугольника равны 45° . | ||||||||||||||||||||
| Прямоугольный треугольник с углом в 30° | ||||||||||||||||||||
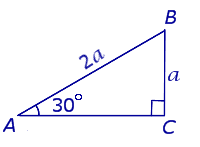 Свойство прямоугольного треугольника с углом в 30° : Катет прямоугольного треугольника, лежащий против угла в 30° , равен половине гипотенузы. Признак прямоугольного треугольника с углом в 30° : Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30° . | ||||||||||||||||||||
| Медиана, проведённая к гипотенузе прямоугольного треугольника | ||||||||||||||||||||
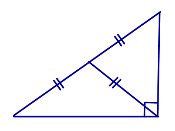 Свойство медианы, проведенной к гипотенузе прямоугольного треугольника: Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы. Признак прямоугольного треугольника: Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным. | ||||||||||||||||||||
| Центр описанной окружности | ||||||||||||||||||||
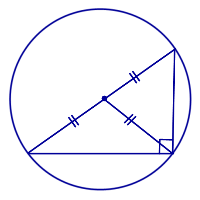 Свойство окружности, описанной около прямоугольного треугольника: Середина гипотенузы прямоугольного треугольника является центром описанной около него окружности. Признак прямоугольного треугольника: Если в треугольнике центр описанной окружности лежит на одной из сторон, то этот треугольник является прямоугольным треугольником, а центр описанной окружности совпадает с серединой гипотенузы. | ||||||||||||||||||||
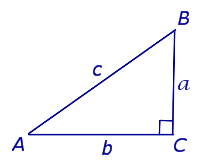 В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов Обратная теорема Пифагора: Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным Содержание Видео:7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать  Прямоугольные треугольникиПрямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов). Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла. Некоторые свойства прямоугольного треугольника:1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов. 2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный. 3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.) 4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$. 5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$ 6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$ 7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника. В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Соотношение между сторонами и углами в прямоугольном треугольнике:В прямоугольном треугольнике $АВС$, с прямым углом $С$ Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет. Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет. 1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. 2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. 3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. 4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему. В прямоугольном треугольнике $АВС$ для острого угла $В$: 5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла. 6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны. 7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения. Значения тригонометрических функций некоторых углов:
Площадь прямоугольного треугольника равна половине произведения его катетов В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√$. Найдите косинус внешнего угла при вершине $В$. Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$: Катет $ВС$ мы можем найти по теореме Пифагора: Подставим найденное значение в формулу косинуса В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sinA=/, AC=9$. Найдите $АВ$. Распишем синус угла $А$ по определению: Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно. Применим теорему Пифагора, чтобы отыскать $«х»$ Так как длина $АВ$ составляет пять частей, то $3∙5=15$ В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$: Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу. В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу. Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе. Видео:Урок 1. Почему катет, лежащий напротив 30 градусов равен половине гипотенузы? №15 ОГЭ.Скачать  Треугольник. Свойство прямоугольного треугольника с углом в 30°.Катет прямоугольного треугольника, противолежащий углу в 30°, будет равняться половине гипотенузы. Изобразим прямоугольный треугольник АСВ с углом В = 30°. В этом случае второй его острый угол будет 60°. Обоснуем, что катет АС равняется половине гипотенузы АВ то есть АС = 1/2АВ. Продлим катет АС за вершину прямого угла С и начертим отрезок СМ, причем части равные СМ=АС. Прочертим ВМ, соединив таким образом точки В и М. Сформированные прямоугольные треугольники ВСМ и АСВ эквиваленты (равны по двум катетам). Наглядно видно, что всякий угол треугольника АМВ по 60°, значит можно сделать вывод, что образовавшийся треугольник — равносторонний. Сторона АС = 1/2 АМ, а поскольку АМ = АВ, а значит и катет АС будет равен 1/2 гипотенузы АВ. 🎥 ВидеоУгол 30 градусов в прямоугольном треугольникеСкачать  Треугольник с углом 30 градусов СоветСкачать  Катет, лежащий напротив угла в 30 градусовСкачать 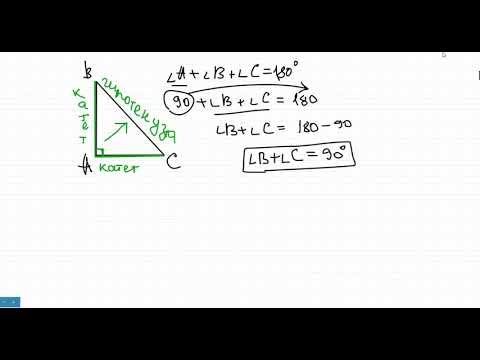 Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать  Свойства прямоугольного треугольника. 7 класс.Скачать  7 класс, 35 урок, Некоторые свойства прямоугольных треугольниковСкачать  Решение задач (прямоугольный треугольник с углом 30 градусов)Скачать  Решение прямоугольных треугольников с углом 30 градусовСкачать  Построить угол 30°Скачать  Урок 22. Свойство катета прямоугольного треугольника, лежащего против угла в 30° (7 класс)Скачать  Построение углов заданной градусной мерыСкачать  Соотношение сторон треугольника 30-60-90 (доказательство)Скачать  Задача о катете треугольника 30, 60, 90Скачать  Угол 30 градусовСкачать  Треугольники с углами 30, 60, 90 градусов. ВведениеСкачать  Угол 30 градусов без угломераСкачать  Замечательный прямоугольный треугольник с углом 30 градусовСкачать  Прямоугольный треугольник с углами "30°- 60°-90°".Скачать  |
