Отрезок cd биссектриса треугольника abc окружность

Видео:Геометрия Отрезок CD биссектриса треугольника ABC Через точку D проведена прямая которая параллельнаСкачать

Разделы

Видео:№538. Биссектриса AD треугольника ABC делит сторону ВС на отрезки CD и BD, равные соответственноСкачать

Дополнительно

Задача по математике — 6845

Отрезок $CD$ — биссектриса треугольника $ABC$. Окружность, проходящая через точки $C$ и $D$ касается стороны $AB$ и пересекает стороны $AC$ и $BC$ в точках $M$ и $N$ соответственно.
а) Докажите, что $MNparallel AB$.
б) Найдите $MN$, если известно, что $AD=2$, $BD=4$ и $AM=1$.

Задача по математике — 6846

Основание и боковая сторона равнобедренного треугольника равны 26 и 38 соответственно.
а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник.
б) Найдите длину отрезка этой средней линии, заключённого внутри окружности.

Задача по математике — 6847

В окружность вписан четырёхугольник с тремя равными сторонами.
а) Докажите, что в этом четырёхугольнике есть параллельные стороны.
б) Найдите диагонали четырёхугольника, если известно, что радиус окружности равен 25, а каждая из трёх равных сторон четырёхугольника равна 30.

Задача по математике — 6848

В выпуклом четырёхугольнике $ABCD$ известно, что $cosangle ABC=-cosangle ADC$.
а) Докажите, что $angle ABD=angle ACD$.
б) Найдите радиус окружности, описанной около этого четырёхугольника, если известно, что $angle ACB=30^$, $BC=6$, а высоты треугольников $ABD$ и $CBD$, проведённые из вершины $B$, равны.

Задача по математике — 6849

Окружность с центром $O$, вписанная в треугольник $ABC$, касается сторон $AB$ и $AC$ в точках $M$ и $N$ соответственно, $AH$ — высота треугольника. Прямые $MN$ и $BC$ пересекаются в точке $K$.
а) Докажите, что $angle MKB=angle OAH$.
б) Найдите $AK$, если известно, что $angle ABC=77^$, $angle ACB=17^$, а отрезок, соединяющий точку $H$ с серединой $MN$, равен 8.

Задача по математике — 6850

На основаниях $AD$ и $BC$ трапеции $ABCD$ построены квадраты $ADEF$ и $BCGH$, расположенные вне трапеции.
а) Докажите, что прямая $FG$ проходит через точку пересечения диагоналей трапеции.
б) Прямая, проходящая через центры квадратов, пересекает основание $BC$ в точке $M$. Найдите $BM$, если известно, что $BC=20$, $ACperp BD$ и $BD:AC=3:2$.

Задача по математике — 6851

Окружность, вписанная в равнобедренную трапецию $ABCD$, касается боковых сторон $AB$ и $CD$ в точках $M$ и $N$ соответственно. Отрезок $AN$ пересекает окружность в точке $K$, а луч $MK$ пересекает основание $AD$ в точке $L$.
а) Докажите, что треугольник $AKL$ подобен треугольнику $MAL$.
б) Найдите отношение $AL:LD$.

Задача по математике — 6852

$AA_$, $BB_$ и $CC_$ — высоты остроугольного треугольника $ABC$ с углом $45^$ при вершине $C$.
а) Докажите, что треугольник $A_B_C_$ прямоугольный.
б) Найдите отношение, в котором высота $AA_$ делит отрезок $B_C_$, если известно, $BC=2B_C_$.

Задача по математике — 6853

Точки $A_$, $B_$ и $C_$ — основания высот треугольника $ABC$, $O$ — центр его описанной окружности.
а) Докажите, что $OAperp B_C_$.
б) Найдите площадь треугольника $ABC$, если известно, что $A_B_=21$, $A_C_=17$, $B_C_=10$.

Задача по математике — 6854

Точки $D$ и $E$ — середины сторон соответственно $AC$ и $BC$ треугольника $ABC$. На отрезке $DE$ как на диаметре построена окружность, пересекающая продолжения сторон $AC$ и $BC$ в точках $M$ и $N$ соответственно.
а) Докажите, что биссектрисы углов $MEN$ и $NDM$ пересекаются на этой окружности.
б) Найдите $MN$, если известно, что $AB=14$, $BC=10$, $AC=6$.

Задача по математике — 6855

Окружность, вписанная в треугольник $ABC$, касается его сторон $BC$, $AC$ и $AB$ в точках $A_$, $B_$ и $C_$ соответственно. В треугольнике $A_B_C_$ проведены высоты.
а) Докажите, что треугольник с вершинами в основаниях этих высот подобен треугольнику $ABC$.
б) Найдите коэффициент подобия, если известно, что радиус вписанной окружности треугольника $ABC$ в три раза меньше радиуса описанной.

Задача по математике — 6856

В прямоугольном треугольнике $ABC$ с гипотенузой $AB$ проведены медианы $AM$ и $BN$. Известно, что около четырёхугольника $ABMN$ можно описать окружность.
а) Докажите, что треугольник $ABC$ равнобедренный.
б) Найдите радиус окружности, описанной около четырёхугольника $ABMN$, если также известно, что $AB=4sqrt$.

Задача по математике — 6857

Во вписанном четырёхугольнике $ABCD$ стороны $BC$ и $CD$ равны. Диагонали четырёхугольника пересекаются в точке $K$.
а) Докажите, что $ACcdot CK=BC^$.
б) Найдите площадь этого четырёхугольника, если известно, что $AC=8$ и $angle BAD=150^$.

Задача по математике — 6858

На каждой стороне равностороннего треугольника взято по точке. Стороны треугольника с вершинами в этих точках соответственно перпендикулярны сторонам исходного треугольника.
а) Докажите, что треугольник с вершинами в указанных точках также равносторонний.
б) Найдите отношение площади этого треугольника к площади исходного

Задача по математике — 6859

На стороне $BC$ треугольника $ABC$ как на диаметре построена окружность, пересекающая отрезок $AB$ в точке $D$. При этом $angle ABC=angle ACD$.
а) Докажите, что прямая $CD$ разбивает треугольник $ABC$ на два подобных треугольника.
б) Найдите отношение площадей этих подобных треугольников, если известно, что $AC=15$, $BC=20$.

Видео:№191. Отрезок ВК — биссектриса треугольника ABC. Через точку К проведена прямая, пересекающаяСкачать

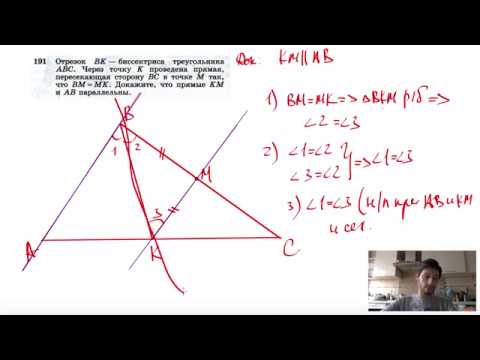
Отрезок СБ — биссектриса треугольника АВС. Через точку Б проведена прямая, которая параллельна прямой АС и пересекает сторону ВС в точке

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Ваш ответ

Видео:Геометрия Биссектриса CM треугольника ABC делит сторону AB на отрезки AM = 17 и MB = 19. КасательнаяСкачать

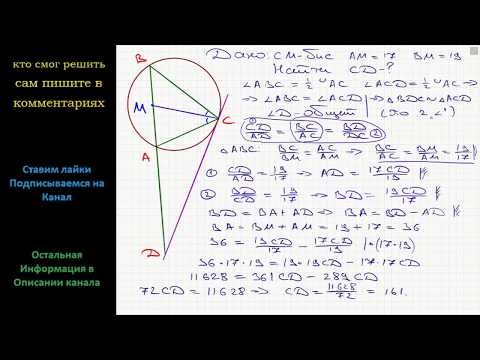
решение вопроса

Видео:Геометрия Отрезок CD биссектриса треугольника ABC в котором угол A = α угол B = β Через точку DСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,921
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

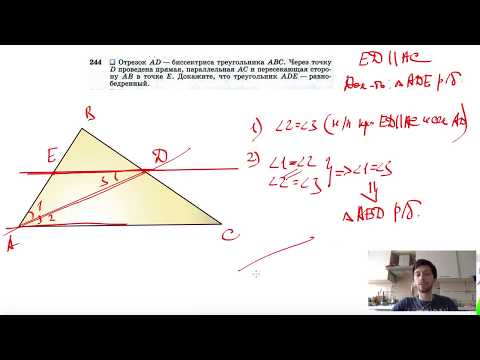
Видео:№244. Отрезок AD — биссектриса треугольника ABC. Через точку D проведена прямая, параллельная АССкачать

Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Видео:№536. Отрезок BD является биссектрисой треугольника ABC. а) Найдите АВ, если ВС = 9 смСкачать

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Видео:Формула для биссектрисы треугольникаСкачать

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

• CD – внутренняя биссектриса ∠ACB;
• CE – биссектриса угла, смежного с ∠ACB;
• ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.

Видео:Геометрия Отрезок AD биссектриса треугольника ABC AB = 6 см AC = 8 см угол BAC = 120 Найдите бисСкачать

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

📹 Видео

Задание 26 ОГЭ по математике #29Скачать

ОГЭ без рекламы математика 17 вариант задача 25Скачать

№537. Отрезок AD является биссектрисой треугольника ABC. Найдите BD и DC, если АВ = 14 смСкачать

№142. Равнобедренные треугольники ADC и BCD имеют общее основание DC. Прямая АВ пересекает отрезокСкачать

№146. Отрезки АВ и CD — диаметры окружности с центром О. Найдите периметр треугольника AOD, еслиСкачать

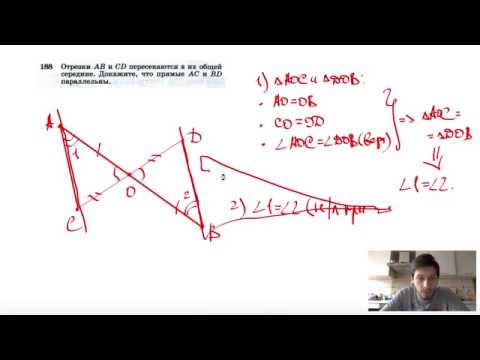
№188. Отрезки АВ и CD пересекаются в их общей середине. Докажите, что прямые АССкачать

№535. Докажите, что биссектриса треугольника делит противоположную сторону на отрезки,Скачать

Задача 26. Вариант 9. ОГЭ по математике 9 класс.Скачать

№144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВССкачать

Свойство биссектрисы треугольника с доказательствомСкачать