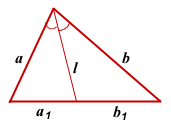
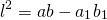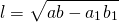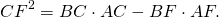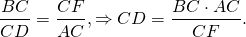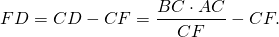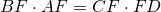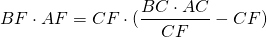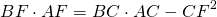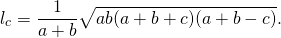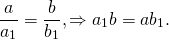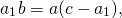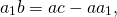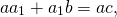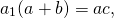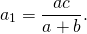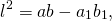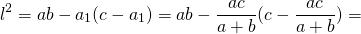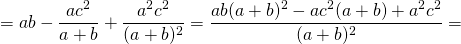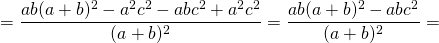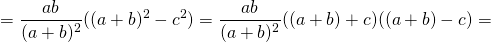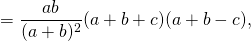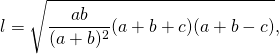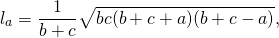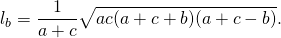Длина биссектрисы треугольника может быть найдена разными способами, в зависимости от исходных данных.
I. Через длины двух сторон и отрезки, на которые биссектриса делит третью сторону.
Квадрат биссектрисы треугольника равен разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.
Соответственно, длина биссектрисы равна квадратному корню из разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.
Дано:
СF — биссектриса ∠ABC
Доказательство:
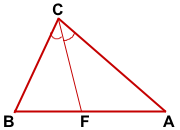
Опишем около треугольника ABC окружность и продлим биссектрису CF до пересечения с окружностью в точке D. Соединим точки A и D отрезком.
Рассмотрим треугольники BCF и DCA.
∠BCF=∠DCA (по условию);
Значит, треугольники BFC и DCA подобны (по двум углам).
Из подобия треугольников следует пропорциональность соответствующих сторон:
Что и требовалось доказать.
II. Через три стороны треугольника
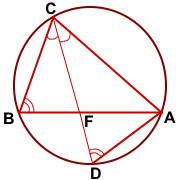
Длина биссектрисы треугольника выражается через длины его сторон a, b и c по формуле
По свойству биссектрисы треугольника:
Согласно утверждению 1,
Что и требовалось доказать.
III Через две стороны треугольника и угол между ними.
Длина биссектрисы треугольника через две стороны, образующие угол, из вершины которого исходит биссектриса, и угол между этими сторонами выражается по формуле
Видео:Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать
Определение и свойства биссектрисы угла треугольника
В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.
Видео:Формула для биссектрисы треугольникаСкачать
Определение биссектрисы угла треугольника
Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.
Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.
Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.
Внешней называется биссектриса угла, смежного с внутренним углом треугольника.
Видео:Длина биссектрисы, проведённой к стороне с треугольника вычисляется по формуле. Найдите биссектрису.Скачать
Свойства биссектрисы треугольника
Свойство 1 (теорема о биссектрисе)
Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):
Свойство 2
Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.
Свойство 3
Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).
Свойство 4
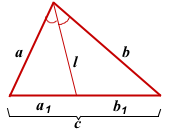
Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):
BD 2 = AB ⋅ BC – AD ⋅ DC
Свойство 5
Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.
- CD – внутренняя биссектриса ∠ACB;
- CE – биссектриса угла, смежного с ∠ACB;
- ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать
Пример задачи
Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.
Решение
Нарисуем чертеж согласно условиям задачи.
Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.
Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):
Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29
Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.
Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.
Видео:Как найти биссектрису в треугольнике? 2 формулы биссектрисыСкачать
Формулы для вычисления длины биссектрисы треугольника
Формулы для вычисления длины биссектрисы треугольника
Можно вывести различные формулы, с помощью которых можно вычислить длину биссектрисы треугольника, если известны:
· длины прилежащих сторон и угол между ними
· длины прилежащих сторон и отрезки, на которые биссектриса разбивает противолежащую сторону
· длины трех сторон треугольника.
Докажем первую из формул.
Задача 1. Вычислить длину биссектрисы треугольника, если известны длинны двух прилежащих сторон треугольника и угол между ними.
Решение. Пусть в треугольнике АВС известно, что
.
Обозначим биссектрису AD через la .
.
Используя формулу синуса двойного угла, получаем:
.
Ответ: .
Выражение 
называется средним гармоническим чисел а и с. Поэтому формулу 
можно запомнить следующим образом:
биссектриса треугольника равна произведению среднего гармонического прилежащих сторон треугольника на косинус половинного угла между ними.
Доказательство остальных формул можно посмотреть, например, в методическом пособии «Опорные задачи по планиметрии».
Задача 2. Вычислите биссектрису треугольника ABC, проведённую из вершины А, если ВС = 18, АС = 15, АВ = 12.
Решение. Воспользуемся формулой для вычисления биссектрисы угла, если известны три стороны треугольника: 
Задача 3. Определить площадь треугольника, если две его стороны равны 35 см и 14 см, а биссектриса угла между ними содержит 12 см.
Пусть в треугольнике АВС АС=35, АВ=14, AD — биссектриса, AD=12.
,
Вычислим 
, получаем:
, 
.
(по основному тригонометрическому тождеству).
Далее по формуле синуса двойного угла вычисляем
.
Для вычисления площади треугольника воспользуемся формулой 
.
Задача 4. . В равнобедренном треугольнике BCD с основанием BD
проведена биссектриса BE. Известно, что СЕ = 20 и DE = 10. Найдите BE.
Используя свойство биссектрисы угла треугольника (урок 4), получаем
, то есть 
.
Таким образом, нам известны длины двух прилежащих сторон и отрезки, на которые биссектриса разбивает противолежащую сторону, поэтому 
Ответ :
.
Задачи для самостоятельного решения
1. Дан треугольник со сторонами 4, 8, 9. Найти длину биссектрисы, проведенной к большей стороне.
2. В треугольнике ABC известно, что АВ = 10, АС = 15, 
BAC = 120°. Найдите биссектрису AD.
3. Катеты прямоугольного треугольника равны 6 и 8. Найдите биссектрису треугольника, проведённую из вершины прямого угла.
4. В равнобедренном треугольнике BCD с основанием BD проведена биссектриса BE. Известно, что СЕ = 18 и DE = 12. Найдите BE.
🎬 Видео
Свойство биссектрисы треугольника с доказательствомСкачать
Первая формула нахождения длины биссектрисы угла треугольника.Скачать
длина биссектрисы #SHORTSСкачать
БИССЕКТРИСА. ДЛИНА БИССЕКТРИСЫ.Скачать
56 Длина биссектрисы треугольникаСкачать
Формула биссектрисы треугольникаСкачать
Свойства биссектрисы. Длина биссектрисы.Скачать
Длина биссектрисы треугольникаСкачать
Длина биссектрисы треугольника.Скачать
Длина биссектрисы. Часть 1.Скачать
Найдите биссектрису треугольникаСкачать
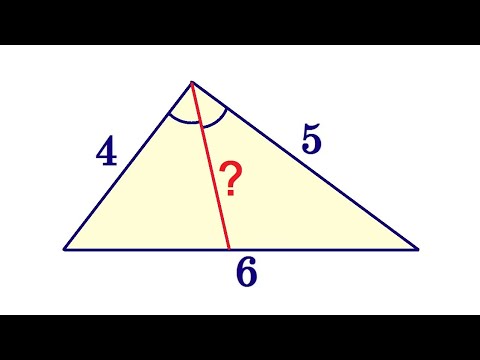
Найди длину биссектрисы. Непростая задача №3Скачать
Длина медианы треугольникаСкачать
Секретные формулы биссектрисы треугольника!😉❤️🔥#математика #егэСкачать
Вычисление длины биссектрисы треугольникаСкачать
