В четырехугольнике abcd на диагонали ac взяты точки

В параллелограмме ABCD на диагонали АС взяты точки К и L так, что AK=1/3AC, CL=0,4AC. Найдите площадь четырехугольника BLDK, если площадь параллелограмма ABCD равна 45.

​ ( S_=0,5*BD*AC*sinw ) ​, где ​ ( w ) ​ — угол между диагоналями, т.е между AC и BD

Тогда площадь ​ ( BLKD ) ​ в ​ ( frac ) ​ раз меньше, чем площадь ​ ( ABCD ) ​

Видео:На окружности по разные стороны от диаметра AB ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

В четырехугольнике abcd на диагонали ac взяты точки

Вариант 1

1. В четырехугольнике ABCD: АВ || CD, ВС || AD, АС = 20 см, BD = 10 см, АВ = 13 см. Диагонали четырехугольника ABCD пересекаются в точке О. Найдите периметр Δ COD.
2. Из вершины В параллелограмма ABCD с острым углом А проведен перпендикуляр ВК к прямой AD; ВК = АВ : 2. Найдите ∠C, ∠D.
3. Середина отрезка BD является центром окружности с диаметром АС, причем точки А, В, С, D не лежат на одной прямой. Докажите, что ABCD – параллелограмм.

Вариант 2

1. В четырехугольнике ABCD АВ || CD, ВС || AD, О – точка пересечения диагоналей. Периметр Δ AOD равен 25 см, АС = 16 см, BD = 14 см. Найдите ВС.
2. В параллелограмме ABCD с острым углом А из вершины В опущен перпендикуляр ВК к прямой AD, AK = ВК. Найдите ∠C, ∠D.
3. Дан параллелограмм ABCD. На продолжении диагонали АС за вершины А и С отмечены точки М и N соответственно так, что AM = CN. Докажите, что MBND – параллелограмм.

II уровень сложности (задания)

Вариант 3

1. В четырехугольнике ABCD ∠А + ∠B = 180°, АВ || CD. На сторонах ВС и AD отмечены точки М и К соответственно так, что ВМ = KD. Докажите, что точки М и К находятся на одинаковом расстоянии от точки пересечения диагоналей четырехугольника.
2. На сторонах РК и МН параллелограмма МРКН взяты точки А и В, соответственно МР = РВ = АК; ∠MPB = 60°. Найдите углы параллелограмма и сравните отрезки ВМ и АН.
3. На основании АС равнобедренного треугольника АВС отмечена точка К, а на сторонах АВ и ВС – точки М и Р соответственно, причем РК = MB, ∠KPC = 80°, ∠C = 50°. Докажите, что КМВР – параллелограмм.

Вариант 4

1. В четырехугольнике МРКН ∠PMK = ∠HKM, РК || МН. Через точку пересечения диагоналей проведена прямая, пересекающая стороны РК и МН в точках А и В соответственно. Докажите, что АР = НВ.
2. На сторонах ВС и AD параллелограмма ABCD взяты точки М и К, АВ = ВМ = KD, ∠AMB = 30°. Найдите угол параллелограмма и сравните отрезки АМ и СК.
3. В треугольнике МРК ∠M = 65°. На сторонах МК, МР, РК отмечены точки А, В, С соответственно так, что середина стороны РК – точка С, AM = КС, BP = АС, ∠BAM = 50°. Докажите, что ВРСА – параллелограмм.

III уровень сложности (задания)

Вариант 5

1. В выпуклом четырехугольнике ABCD ∠A + ∠B = ∠B + ∠C = = 180°. Через точку О пересечения диагоналей четырехугольника проведена прямая, пересекающая стороны ВС и AD в точках М и К соответственно; ∠BOM = 90°. Докажите, что KD = ВМ.
2. На сторонах ВС и CD параллелограмма ABCD отмечены точки М и Н соответственно так, что отрезки ВН и MD пересекаются в точке О; ∠BHD = 95°, ∠DMC = 90°, ∠BOD = 155°. Найдите отношение длин отрезков АВ и MD и углы параллелограмма.
3. Точки М и К являются соответственно серединами сторон АВ и ВС треугольника АВС. Через вершину С вне треугольника проведена прямая, параллельная АВ и пересекающая луч МК в точке Е. Докажите, что КЕ = АС : 2.

Вариант 6

1. В выпуклом четырехугольнике МРКН ∠M + ∠P = 180°, ∠MKH = ∠KMP. На сторонах МН и РК отмечены точки А и В так, что РВ = РА. Отрезок АВ проходит через точку пересечения диагоналей четырехугольника. Докажите, что HP ⊥ АВ.
2. На сторонах ВС и CD параллелограмма ABCD взяты точки К и М соответственно. Отрезки ВМ и KD пересекаются в точке О; ∠BOD = 140°, ∠DKB = 110°, ∠BMC = 90°. Найдите отношение длин отрезков МС и AD и углы параллелограмма.
3. Точки А и В принадлежат соответственно сторонам РЕ и ЕТ треугольника РЕТ. Прямая, проходящая через вершину Т вне треугольника, пересекает луч АВ в точке К так, что АР = КТ, АВ = ВК= РТ : 2. Докажите, что точка А является серединой отрезка РЕ.

Геометрия 8 Атанасян Самостоятельная 2. ОТВЕТЫ

I уровень сложности (ответы)

Вариант 1

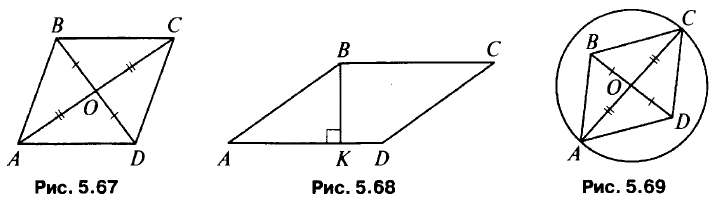
1. ABCD – параллелограмм (рис. 5.67), тогда CD = АВ = 13 см, ОС = АО = 10 см, BD = OD = 5 см (объясните). P_COD = 10 + 5 + 13 = 28 см.
2. ВК = АВ/2 (рис. 5.68), тогда ∠A = 30° (объясните), значит, ∠C = 30°, ∠D = 150° (объясните).
3. В четырехугольнике ABCD (рис. 5.69) середину отрезка BD отметим точкой О. Отсюда следует, что BO = OD.
   Одновременно точка О является центром окружности с диагональю AC, следовательно AO = OC.
   По свойству параллелограммов (диагонали пересекаются и точкой пересечения делятся пополам), если BO = OD и AO = OC, то ABCD – параллелограмм.

Вариант 2

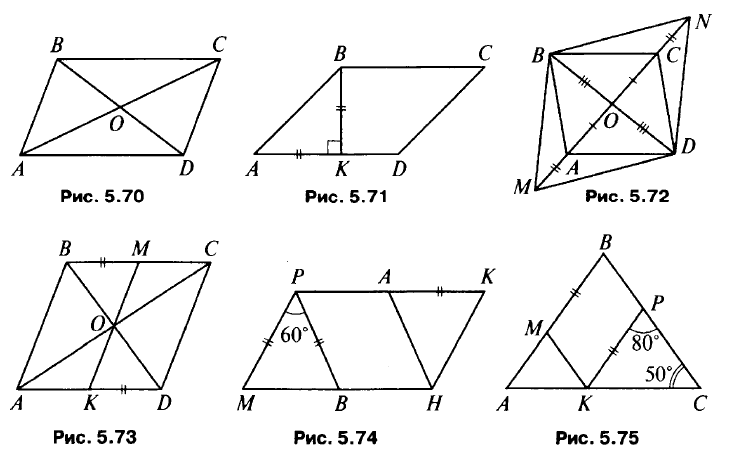
1. ABCD – параллелограмм (рис. 5.70), тогда АО = СО = 8 см, ВО = DO = 7 см (объясните). Так как P_AOD = 25 см, то ВС = AD = 10 см.
2. AK = ВК (рис. 5.71), тогда ∠A = 45° (объясните), ∠C = 45°, ∠D = 135° (объясните).
3. ABCD – параллелограмм (рис. 5.72), тогда АО = СО, ВО = DO. В четырехугольнике MBND диагонали точкой пересечения делятся пополам, значит, MBND – параллелограмм.

II уровень сложности (ответы)

Вариант 1

1. (рис. 5.73) а) Докажите, что ABCD – параллелограмм и ВС || AD. б) Докажите, что ΔBOM = ΔDOK и ОМ = ОК.
2. (рис. 5.74) а) Докажите, что ΔМРВ – равносторонний, ∠M = 60°, ∠K = 60. б) Докажите, что ΔАКН – равносторонний, ΔАКН = ΔМРВ, тогда МВ = АН, ∠M = ∠K = 60°, ∠P = ∠H = 120°.
3. (рис. 5.75) а) Найдите ∠B и докажите, что МВ || КР. б) Докажите, что МВРК – параллелограмм.

Вариант 2

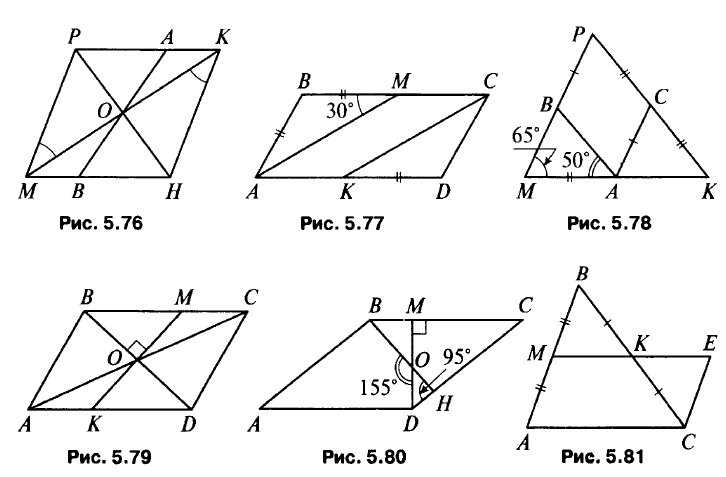
1. (рис. 5.76) а) Докажите, что МРКН – параллелограмм и РО = НО. б) Докажите, что ΔРОА = ΔНОВ и РА = НВ.
2. (рис. 5.77) а) Докажите, что ΔАВМ – равнобедренный, ∠B = 120°, ∠BAD = 60°. б) Докажите, что ΔАВМ = ΔKDC и AM = КС, ∠B = ∠D = 120°, ∠14 = ∠C = 60°.
3. (рис. 5.78.) а) Докажите, что в ΔАВМ МА = ВА. б) Докажите, что ВРСА – параллелограмм.

III уровень сложности (ответы)

Вариант 1

1. (рис. 5.79) а) Докажите, что ΔBCD – параллелограмм и АО = СО. б) Докажите, что ΔАОК = ΔСОМ и КО = МО. в) Докажите, что ΔDKO = ΔВМО и KD = ВМ.
2. (рис. 5.80) ∠MDC = 60°, ∠MCD = 30° (объясните). MD = CD/2, AB : MD = 2 : 1, ∠C = ∠A = 30°, ∠B = ∠D = 150°.
3. (рис. 5.81) а) Докажите, что ΔMВК = ΔЕСК и ЕС = МВ = AM, КЕ = МК = ME/2; б) Докажите, что АМЕС – параллелограмм и ME = АС, т. е. КЕ = АС/2.

Вариант 2

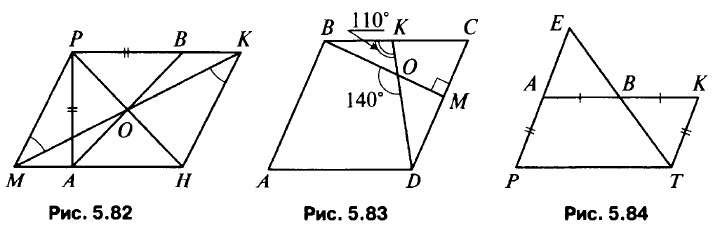
1. (рис. 5.82) а) Докажите, что МРКН – параллелограмм и МО = ОК. б) Докажите, что ΔMОА = ΔКОВ и АО = ОВ. в) Докажите, что РО⊥АВ и PH⊥АВ.
2. (рис. 5.83) ∠KDC = 50°, ∠MCB = 60°, ∠CBM = 30° (объясните). СМ = ВС/2; МС : AD = 1 : 2; ∠C = ∠A = 60°, ∠B = ∠D = 120°.
3. (рис. 5.84) а) Докажите, что РАКТ – параллелограмм и РЕ || КТ. б) Докажите, что ΔАЕВ = ΔКТВ и АЕ = КТ = РА, т. е. А – середина РЕ.

Вы смотрели: Геометрия 8 класс (УМК Атанасян и др. — Просвещение). Урок 4. Самостоятельная работа № 2 «Параллелограмм» с ответами (3 уровня сложности по 2 варианта в каждом). Геометрия 8 Атанасян Самостоятельная 2. Ориентировано на работу с базовым учебником: «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение». В учебных целях использованы цитаты из пособия «Поурочные разработки по геометрии. 7 класс / Гаврилова Н.Ф. — М.: ВАКО».

Видео:2017 на окружности по разные стороны от диаметра AB взяты Точки M и NСкачать

В четырехугольнике abcd на диагонали ac взяты точки

Видео:№382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать

Разделы

Видео:№383 На диагонали BD параллелограмма ABCD отмечены две точки Р и Q так, что PB=QD. ДокажитеСкачать

Дополнительно

Задача по математике — 6314

Пусть $K$, $L$, $M$, $N$ — середины сторон $AB$, $BC$, $CD$, $AD$ выпуклого четырёхугольника $ABCD$; отрезки $KM$ и $LN$ пересекаются в точке $O$. Докажите, что

Задача по математике — 6315

На сторонах $AB$ и $CD$ четырёхугольника $ABCD$ взяты точки $M$ и $N$ так, что $AM:MB=CN:ND$. Отрезки $AN$ и $DM$ пересекаются в точке $K$, а отрезки $BN$ и $CM$ — в точке $L$. Докажите, что $S_=S_+S_$.

Задача по математике — 6316

На стороне $AB$ четырёхугольника $ABCD$ взяты точки $A_$ и $B_$, а на стороне $CD$ — точки $C_$ и $D_$, причём $AA_=BB_=pAB$ и $CC_=DD_=pCD$, где $pltfrac$. Докажите, что $frac<S_<A_B_C_D_>><S_>=1-2p$.

Задача по математике — 6317

Каждая из сторон выпуклого четырёхугольника разделена на пять равных частей, и соответствующие точки противоположных сторон соединены. Докажите, что площадь среднего (заштрихованного) четырёхугольника в 25 раз меньше площади исходного.

Задача по математике — 6318

Точка $O$, лежащая внутри правильного шестиугольника, соединена с вершинами. Возникшие при этом шесть треугольников раскрашены попеременно в красный и синий цвет. Докажите, что сумма площадей красных треугольников равна сумме площадей синих.

Задача по математике — 6319

В треугольнике $ABC$ известно, что $AB=c$, $BC=a$, $AC=b$. В каком отношении центр вписанной окружности треугольника делит биссектрису $CD$?

Задача по математике — 6320

В треугольнике $ABC$ известно, что $AB=c$, $BC=a$, $AC=b$; $O$ — центр окружности, касающейся стороны $AB$ и продолжений сторон $AC$ и $BC$, $D$ — точка пересечения луча $CO$ со стороной $AB$. Найдите отношение $frac$.

Задача по математике — 6321

На сторонах $AB$ и $AC$ треугольника $ABC$ расположены точки $K$ и $L$, причём $AK:KB=4:7$ и $AL:LC=3:2$. Прямая $KL$ пересекает продолжение стороны $BC$ в точке $M$. Найдите отношение $CM:BC$.

Задача по математике — 6322

Точки $M$ и $N$ расположены соответственно на сторонах $BC$ и $AB$ треугольника $ABC$, причём $CM:MB=1:5$ и $BN:AN=1:3$. Прямая $MN$ пересекает продолжение стороны $AC$ в точке $K$. Найдите отношение $CK:AC$.

Задача по математике — 6323

На боковых сторонах $AB$ и $CD$ трапеции $ABCD$ расположены точки $M$ и $N$ соответственно, причём $BM:AM=CN:ND=3:5$. Найдите $MN$, если $BC=a$ и $AD=b$.

Задача по математике — 6324

На диагоналях $AC$ и $BD$ трапеции $ABCD$ с основаниями $BC=a$ и $AD=b$ расположены точки $K$ и $L$ соответственно, причём $CK:KA=BL:LD=7:4$. Найдите $KL$.

Задача по математике — 6325

Точки $P$ и $Q$ расположены соответственно на диагоналях $AC$ и $BD$ трапеции $ABCD$, причём $CP:AP=BQ:DQ=5:2$. Найдите $PQ$, если известно, что основания $AD$ и $BC$ трапеции равны $a$ и $b$ соответственно.

Задача по математике — 6326

Точки $M$ и $N$ расположены соответственно на диагоналях $BD$ и $AC$ трапеции $ABCD$, причём $BM:MD=CN:NA=1:8$. Найдите $MN$, если известно, что основания $AD$ и $BC$ трапеции равны $a$ и $b$ соответственно.

Задача по математике — 6327

На сторонах $AB$ и $BC$ параллелограмма $ABCD$ расположены точки $N$ и $M$ соответственно, причём $AN:NB=3:2$, $BM:MC=2:5$. Прямые $AM$ и $DN$ пересекаются в точке $O$. Найдите отношения $OM:OA$ и $ON:OD$.

Задача по математике — 6328

На сторонах $AD$ и $CD$ параллелограмма $ABCD$ расположены точки $M$ и $N$ соответственно, причём $AM:MD=2:7$, $CN:ND=3:5$. Прямые $CM$ и $BN$ пересекаются в точке $O$. Найдите отношения $ON:OB$ и $OC:OM$.

📸 Видео

#6warmup. Разбор шестой разминкиСкачать

Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC = 12, AB = 7. Найдите DO.Скачать

Геометрия В выпуклом четырёхугольнике ABCD известны стороны и диагональ: AB = 3, BC = CD = 5, AD = 8Скачать

№1039. Диагонали квадрата ABCD пересекаются в точке О. Найдите угол между векторами: а) АВ и АССкачать

Параллелограмм. Практическая часть - решение задачи. 8 класс.Скачать

Геометрия Диагонали четырёхугольника ABCD, вершины которого расположены на окружности, пересекаютсяСкачать

№437. На диагонали АС квадрата ABCD взята точка М так, что AM =АВ. Через точку М проведена прямаяСкачать

Геометрия Через середину диагонали AC параллелограмма ABCD проведена прямая, пересекающая стороныСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

Геометрия На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что угол NBAСкачать

8 класс, 4 урок, ПараллелограммСкачать

№403. В прямоугольнике ABCD диагонали пересекаются в точке О. Найдите периметрСкачать

Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать