Физический смысл градиента вектора (4 видео)

Градиент скалярного поля и его физический смысл

В заключение рассмотрим меру скалярного поля, называемую градиентом, что в переводе с латинского означает шагающий или растущий. Термин впервые появился в метеорологии, а в математику и физику был введен Джеймсом Максвеллом, который предложил его обозначение в виде — grad.

Градиент — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой физической величины, значение которой меняется от одной точки скалярного поля к другой, а по величине (модулю) равный быстроте роста этой величины в этом направлении.

Для раскрытия физического смысла градиента, рассмотрим пример скалярного поля, в котором изменяется один параметр — высота поверхности земли над уровнем моря (см. рис. 2.7). Тогда градиент в каждой точке поверхности будет показывать «направление самого крутого подъема», и своей величиной характеризовать крутизну склона.

Рисунок 2.7 — Пример скалярного поля и его градиента.

Из рисунка видно, что операция градиента преобразует холм (слева), если смотреть на него сверху, в поле векторов (справа). Видно, что векторы направлены «в горку» и тем длиннее, чем круче наклон.

С математической точки зрения градиент — это производная скалярной функции, определенной на векторном пространстве. Для случая трехмерного пространства градиентом скалярной функции

Использовав в качестве единичных векторов векторы (орты) еЛЛ- 110 осям прямоугольных декартовых координат, получаем

В общем, размерность вектора градиента определяется размерностью пространства (или многообразия), на котором задано скалярное поле, о градиенте которого идет речь.

Математический смысл градиента любой скалярной функции/в том, что его скалярное произведение с бесконечно малым вектором перемещения dx дает полный дифференциал этой функции при соответствующем изменении координат в пространстве, на котором определена/, то есть линейную часть изменения / при смещении на dx. Применяя одну и ту же букву для обозначения функции от вектора и соответствующей функции от его координат, можно написать:

Стоит здесь заметить, что поскольку формула полного дифференциала не зависит от вида координат лт.е. от природы параметров х вообще, то полученный дифференциал является инвариантом, то есть скаляром, при любых преобразованиях координат. В тоже время dx — это вектор, то градиент, вычисленный обычным образом, оказывается ковариантным вектором, т.е. вектором, представленным в дуальном базисе, какой только и может дать скаляр при простом суммировании произведений координат обычного (контравариантного) вектора, т.е. вектором, записанным в обычном базисе.

В различных отраслях физики используется понятие градиента различных физических полей. Например, напряженность электростатического поля есть минус градиент электрического потенциала, напряженность гравитационного поля (ускорение свободного падения) в классической теории гравитации есть минус градиент гравитационного потенциала. Консервативная сила в классической механике есть минус градиент потенциальной энергии.

Видео:Оператор набла (оператор Гамильтона) и оператор ЛапласаСкачать

Градиент

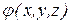
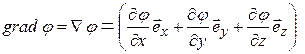
По определению градиентом скалярной функции называется вектор

. (13.01)

Следует помнить о том, что градиента векторной функции не существует, в силу того, что он просто не определен. Можно рассматривать градиент модуля вектора, но модуль – это скалярная величина.

Физический смысл градиента функции заключается в том, что это вектор, направленный в сторону скорейшего возрастания функции, а по модулю равный производной, взятой вдоль направления скорейшего возрастания.

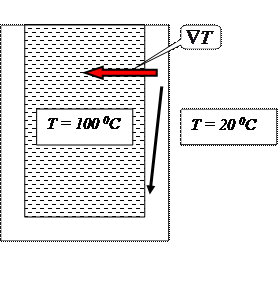
НАПРИМЕР, если в стакан налит кипяток, то, очевидно, что в стенках стакана устанавливается градиент температуры. Поскольку градиент направлен в сторону скорейшего возрастания величины, то градиент температуры перпендикулярен стенкам стакана. Температура изменяется и вдоль направления черной стрелки, но направление СКОРЕЙШЕГО возрастания задается, очевидно, красной.

Величину градиента грубо можно оценить, разделив известное изменение величины на расстояние на котором оно происходит, если это расстояние в направлении скорейшего изменения.

Пока стенки не прогрелись по толщине, можно считать, что на внутренней поверхности температура 100 0 С, а на внешней – в соответствии с температурой окружающей среды – 20 0 С. Если толщина стенок 1 мм, то градиент по модулю равен 80 0 С/мм = 8 10 4 0 С/м. По мере прогревания стенок температура воды в стакане немного упадет, но на внешней поверхности – сильно возрастет. Разница температур уменьшится и градиент по модулю тоже.

Сравним понятия градиент и скорость. Когда мы говорим «скорость изменения некоторой величины равна…», то обычно подразумеваем, что речь о быстроте изменения величины во времени. Говоря о том, что градиент некоторой величины составляет столько-то, мы говорим о быстроте изменения величины в пространстве, т.е. при изменении пространственных координат.

Дата добавления: 2015-09-14 ; просмотров: 3624 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:ДивергенцияСкачать

Электронная библиотека

Полем называется область пространства, каждой точке Р которой поставлена в однозначное соответствие некоторая величина Q(p).

Если величина Q(p) является физической, то поле называется физическим. В зависимости от природы функции Q(p), поля разделяются на скалярные и векторные. Примерами скалярных физических полей могут быть поля температуры, атмосферного давления, плотности воздуха, электрического потенциала, массы и т.д. К векторным величинам относятся: поля силы тяжести, скорости частиц текущей жидкости (газа), сдвига точек упругого тела, магнитной индукции и др.

Если функция Q(p) не изменяется с течением времени, то поле называется стационарным или установившимся, в противном случае – нестационарным.

Для получения общих результатов, справедливых для любых конкретных физических полей, всякому полю ставится в соответствие его математическая модель. Математическая теория поля изучает свойства векторных и скалярных полей, которые выявляются практическими задачами из физики, электротехники, математики и других наук.

Для успешного овладения теорией поля необходим математический аппарат, в который входит векторная алгебра и векторный анализ, элементы дифференциального и интегрального исчисления. Отметим, что в перспективе обобщением теории скалярных и векторных полей является теория тензорных полей, которая играют важную роль в теории упругости, теории относительности и др.

Для задания скалярного поля надо задать скалярную функцию . Введем понятие поверхности (линии) равного уровня скалярного поля.

Определение. Поверхностью равного уровня скалярного поля называется такая поверхность, на которой функция имеет постоянное значение.

Уравнение поверхности уровня:

где С – постоянная. Если функция , то говорят о линии равного уровня: .

При различных значениях С получаем семейство поверхностей (линий) уровня. Примерами поверхностей уровня являются поверхности: равных температур в некотором теле; равного потенциала V в электрическом поле .

Совокупность поверхностей (линий) уровня дает наглядное представление конкретного поля, что облегчает его изучение.

Найти поверхность уровня поля , проходящую через точку .

Решение. Уравнение поверхности уровня: U = C:

Очевидно, . Поверхностями уровня служит семейство сфер с центром в начале координат. Чтобы выбрать нужную сферу, проходящую через , требуется подставить координаты этой точки в уравнение поверхностей уровня:

Уравнение искомой поверхности уровня:

описывает сферу радиуса R = 3 с центром в начале координат.

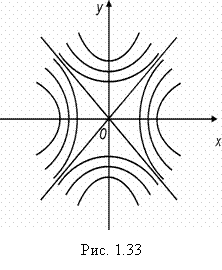
Найти линии уровня поля .

При С > 0 линии уровня есть равнобочные гиперболы с вершинами на оси Ох; при С = 0 – прямые – асимптоты этих гипербол (сопряженных) (рис. 1.33).

Понятие скалярного поля тесно связано с важным понятием производной скалярной функции по заданному направлению (в математическом анализе этого не было).

Теорема: если функция дифференцируема в точке Р, то производная в точке Р по любому направлению существует и равна (обозначается ):

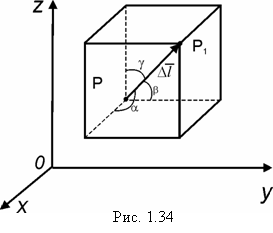
Доказательство. Как известно из математического анализа [6], если функция дифференцируема, то её приращение (рис.

Разделим на обе части последнего равенства, получим:

Переходя к пределу при , и учитывая, что

получим формулу (1.91). Если , то поле возрастает; при – убывает и – дает скорость изменения поля в направлении .

Найти производную от функции по направлению от точки Р(1; 1; 1) к точке Р₁(2; 3; 4).

Формула (1.91) ставит задачу: найти то направление, которое доставляет максимальное значение для . Оказывается, такое направление дается понятием градиента скалярного поля.

Определение. Градиентом скалярного поля (обозначается grad U) называется вектор, проекции которого на оси декартовой системы координат есть , , , т.е.

Вывод: градиент скалярного поля есть вектор.

Имеется связь между производной по направлению и градиентом (рис. 1.35).

Найдем скалярное произведение :

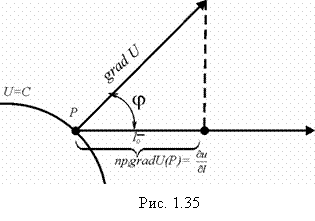
Таким образом, левая часть полученного равенства есть .

При изменении будет меняться и . Очевидно, эта проекция будет максимальной, когда направление совпадает с . Учитывая физический смысл производной по направлению и формулу (1.94) убеждаемся в том, что: вектор grad U по величине и направлению есть наибольшая скорость возрастания . В этом состоит физический смысл градиента. Это широко используется в практике.

Покажем, что направлен по нормали к поверхности (линии) уровня скалярного поля , проходящей через точку Р.

Уравнение поверхности уровня: . Уравнение нормали к поверхности уровня:

где X, Y, Z – текущие координаты нормали; x, y, z – координаты поверхности, в которой проведена нормаль. Видим, что проекции направляющего вектора нормали те же, что и градиента.

Найти наибольшую скорость возрастания скалярного поля в точке Р(1; 2; 3).

Решение. Согласно (1.92) имеем:

Поверхность уровня поля U, проходящая через точку Р(1; 2; 3) – сфера: . Наибольшая скорость возрастания функции U будет в направлении радиуса этой сферы, проходящего через данную точку Р(1; 2; 3).

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00