В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.
Введем некоторые определения.
Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:
e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )
Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.
Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.
Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.
Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.
Переставив местами в исходной системе другие векторы, получим еще один базис.
Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.
Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.
Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.
Рассмотрим применение данной теории на конкретных примерах.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 )
Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.
Решение
Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.
A = 3 2 3 — 2 1 — 1 1 2 — 2 A = 3 — 2 1 2 1 2 3 — 1 — 2 = 3 · 1 · ( — 2 ) + ( — 2 ) · 2 · 3 + 1 · 2 · ( — 1 ) — 1 · 1 · 3 — ( — 2 ) · 2 · ( — 2 ) — 3 · 2 · ( — 1 ) = = — 25 ≠ 0 ⇒ R a n k ( A ) = 3
Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.
Ответ: указанные векторы являются базисом векторного пространства.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 ) d = ( 0 , 1 , 2 )
Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.
Решение
Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , — 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , — 1 , — 2 ) является базисом.
Ответ: указанная система векторов не является базисом.
Исходные данные: векторы
a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )
Могут ли они являться базисом четырехмерного пространства?
Решение
Cоставим матрицу, используя в качестве строк координаты заданных векторов
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
По методу Гаусса определим ранг матрицы:
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
1 2 3 3 0 1 0 2 0 1 — 1 1 0 1 — 2 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 — 2 — 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4
Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.
Ответ: заданные векторы являются базисом четырехмерного пространства.
Исходные данные: векторы
a ( 1 ) = ( 1 , 2 , — 1 , — 2 ) a ( 2 ) = ( 0 , 2 , 1 , — 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )
Составляют ли они базис пространства размерностью 4?
Решение
Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.
Ответ: нет, не составляют.
- Разложение вектора по базису
- Связь между базисами
- Учебное пособие: Методические указания для студентов 1 курса Одесса 2008
- Ортогональный и ортонормированный базисы евклидова пространства
- Выражение скалярного произведения через координаты сомножителей
- Преимущества ортонормированного базиса
- Изменение матрицы Грама при переходе от одного базиса к другому
- Свойства определителя Грама
- Изоморфизм евклидовых пространств
- 🎦 Видео
Видео:Линейная оболочка. Базис и размерностьСкачать

Разложение вектора по базису
Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.
Таким образом, мы пришли к формулировке важнейшей теоремы:
Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.
Докажем эту теорему:
зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :
x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.
Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:
Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:
1 — x 1 ) · e ( 1 ) + ( x
2 — x 2 ) · e ( 2 ) + . . . ( x
Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x
2 — x 2 ) , . . . , ( x
n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x
n . И это доказывает единственный вариант разложения вектора по базису.
При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .
Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.
Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .
Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.
Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x
Вектор x → будет представлен следующим образом:
2 · e ( 2 ) + . . . + x
Запишем это выражение в координатной форме:
( x 1 , x 2 , . . . , x n ) = x
1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x
2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x
n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x
2 e 1 ( 2 ) + . . . + x
2 e 2 ( 2 ) + + . . . + x
n e 2 ( n ) , . . . , x
2 e n ( 2 ) + . . . + x
Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x
n e 2 n ⋮ x n = x
Матрица этой системы будет иметь следующий вид:
e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )
Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x
n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .
Применим рассмотренную теорию на конкретном примере.
Исходные данные: в базисе трехмерного пространства заданы векторы
e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )
Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.
Решение
Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .
Используем метод Гаусса:
A = 1 — 1 1 3 2 — 5 2 1 — 3
1 — 1 1 0 5 — 8 0 3 — 5
1 — 1 1 0 5 — 8 0 0 — 1 5
R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.
Пусть в базисе вектор x → имеет координаты x
3 . Связь этих координат определяется уравнением:
3 e 1 ( 3 ) x 2 = x
3 e 2 ( 3 ) x 3 = x
Применим значения согласно условиям задачи:
Решим систему уравнений методом Крамера:
∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x
1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x
1 ∆ = — 1 — 1 = 1 ∆ x
2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x
2 ∆ = — 1 — 1 = 1 ∆ x
3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x
Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x
Ответ: x = ( 1 , 1 , 1 )
Видео:Процесс ортогонализации Грама-Шмидта. ПримерСкачать

Связь между базисами
Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:
c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
Указанные системы являются также базисами заданного пространства.
n ( 1 ) — координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:
1 ( 1 ) e 1 ( 1 ) + c
2 ( 1 ) e 1 ( 2 ) + . . . + c
n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c
1 ( 1 ) e 2 ( 1 ) + c
2 ( 1 ) e 2 ( 2 ) + . . . + c
n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c
1 ( 1 ) e n ( 1 ) + c
2 ( 1 ) e n ( 2 ) + . . . + c
В виде матрицы систему можно отобразить так:
( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c
n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Сделаем по аналогии такую же запись для вектора c ( 2 ) :
( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c
n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
И, далее действуя по тому же принципу, получаем:
( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c
n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Матричные равенства объединим в одно выражение:
c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c
n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )
Оно и будет определять связь векторов двух различных базисов.
Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :
e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e
n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )
Дадим следующие определения:
n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )
к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .
n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )
к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .
Видео:Как разложить вектор по базису - bezbotvyСкачать

Учебное пособие: Методические указания для студентов 1 курса Одесса 2008
| Название: Методические указания для студентов 1 курса Одесса 2008 Раздел: Остальные рефераты Тип: учебное пособие Добавлен 17:40:19 17 сентября 2011 Похожие работы Просмотров: 2273 Комментариев: 8 Оценило: 1 человек Средний балл: 2 Оценка: неизвестно Скачать |
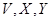 — произвольные пространства над некоторым полем
— произвольные пространства над некоторым полем 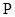 ;
;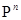 — пространство
— пространство 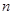 — мерных строк (столбцов) с элементами из поля
— мерных строк (столбцов) с элементами из поля 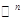 — действительное
— действительное 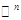 — комплексное
— комплексное 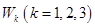 — пространства геометрических векторов (прямой, плоскости, пространства);
— пространства геометрических векторов (прямой, плоскости, пространства);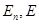 — евклидовы пространства (с указанием размерности или без него);
— евклидовы пространства (с указанием размерности или без него);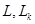 — подпространства данного пространства (
— подпространства данного пространства (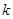 — индекс, не связанный с размерностью);
— индекс, не связанный с размерностью);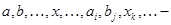 векторы рассматриваемого пространства;
векторы рассматриваемого пространства; 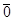 — нулевой вектор;
— нулевой вектор;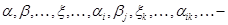 скаляры из данного поля,
скаляры из данного поля,  — нуль этого поля;
— нуль этого поля;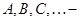 линейные операторы, в отдельных случаях – матрицы;
линейные операторы, в отдельных случаях – матрицы;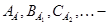 матрицы линейных операторов в базисах соответственно
матрицы линейных операторов в базисах соответственно 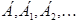 ;
;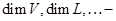 размерности пространств
размерности пространств 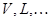 ;
;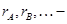 ранги операторов (матриц)
ранги операторов (матриц) 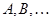 ;
; скалярное произведение в данном пространстве;
скалярное произведение в данном пространстве; векторное произведение в данном пространстве
векторное произведение в данном пространстве  .
. векторов пространства
векторов пространства 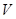 над полем
над полем 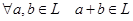 ,
,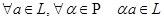 .
.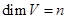 , а
, а 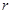 условий специального вида, то есть основания ожидать, что
условий специального вида, то есть основания ожидать, что 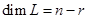 .
.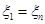 , поэтому
, поэтому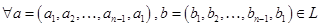
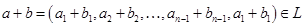 ,
,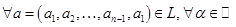
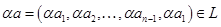 .
.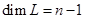 . Для этого рассмотрим векторы стандартного базиса
. Для этого рассмотрим векторы стандартного базиса 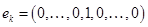
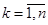 . Векторы
. Векторы 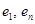 не принадлежат
не принадлежат 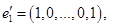
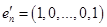 . Рассмотрим систему векторов
. Рассмотрим систему векторов 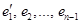 . Она образует базис
. Она образует базис 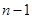 , то и
, то и 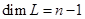 . Итак, наше предположение оказалось верным.
. Итак, наше предположение оказалось верным.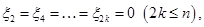 поэтому следует ожидать, что
поэтому следует ожидать, что 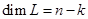 , где
, где 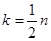 , если
, если 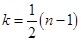 , если
, если 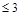 (
(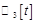 ).
).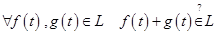 .
.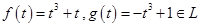 , тогда
, тогда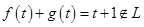 ,
,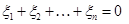 .
.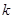 . Однако, замена на векторах
. Однако, замена на векторах 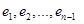 последнего нуля числом (-1) дает нам векторы из
последнего нуля числом (-1) дает нам векторы из 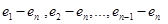
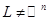 и, следовательно,
и, следовательно, 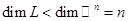 .
.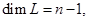
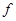 — неотрицательная квадратичная форма от
— неотрицательная квадратичная форма от 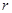 . Доказать, что все решения уравнения
. Доказать, что все решения уравнения 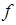 =0 образуют
=0 образуют 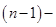 мерное линейное подпространство пространства
мерное линейное подпространство пространства 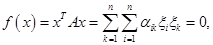
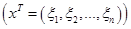 , никак не указывают на способ решения задачи.
, никак не указывают на способ решения задачи.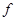 . Нормальный вид такой формы
. Нормальный вид такой формы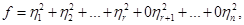 (1)
(1)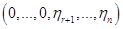 , (2)
, (2)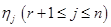 — произвольные числа из
— произвольные числа из 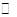 . Имеющийся опыт (задача 1.2) подсказывает, что множество векторов такого вида есть (
. Имеющийся опыт (задача 1.2) подсказывает, что множество векторов такого вида есть (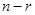 )-мерное подпространство пространства
)-мерное подпространство пространства 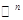 . Но данная нам форма не обязательно нормальная. И здесь мы вспоминаем, что каждая неотрицательно определенная форма ранга
. Но данная нам форма не обязательно нормальная. И здесь мы вспоминаем, что каждая неотрицательно определенная форма ранга 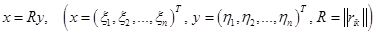 , приводящее форму
, приводящее форму 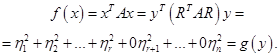
 состоит из векторов
состоит из векторов 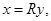 где
где 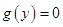 , то есть из векторов
, то есть из векторов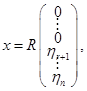
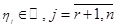 .
.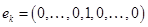 (1 на
(1 на 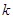 — ой позиции) и докажем, что множество
— ой позиции) и докажем, что множество 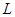 решений уравнения
решений уравнения 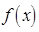 =0 есть линейная оболочка системы векторов
=0 есть линейная оболочка системы векторов 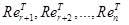
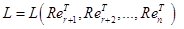 .
.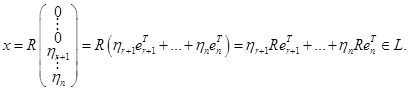
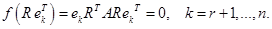
 линейно независима (проверяется непосредственно). Составляем линейную комбинацию
линейно независима (проверяется непосредственно). Составляем линейную комбинацию 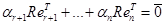 . Получаем
. Получаем 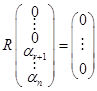 . Мы пришли к матричному уравнению, которое имеет единственное решение, так как матрица
. Мы пришли к матричному уравнению, которое имеет единственное решение, так как матрица 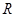 является невырожденной.
является невырожденной.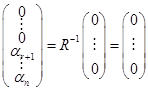 .
.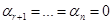 . Тем самым мы показали, что система
. Тем самым мы показали, что система 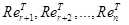 является линейно независимой. Следовательно,
является линейно независимой. Следовательно, 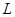 — линейное пространство (по построению) и его размерность
— линейное пространство (по построению) и его размерность 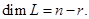
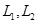 — данные подпространства пространства. Обычно их задают в виде линейных оболочек систем векторов или как множества решений некоторых однородных систем линейных уравнений, а сами векторы- координатными строками в некотором базисе. Вычисление
— данные подпространства пространства. Обычно их задают в виде линейных оболочек систем векторов или как множества решений некоторых однородных систем линейных уравнений, а сами векторы- координатными строками в некотором базисе. Вычисление 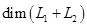 не составляет особого труда: это ранг объединения базисов или порождающих систем подпространств
не составляет особого труда: это ранг объединения базисов или порождающих систем подпространств 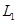 и
и 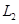 .
. 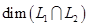 находится по формуле
находится по формуле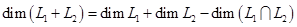 . (3)
. (3)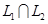 . В общем виде этот вопрос рассматривается в задаче №1319 [4]. Здесь же мы укажем, как найти решения конкретных задач (№№ 1320-1322 [4]). Задачу 1.6 мы решим двумя способами, второй — с помощью схемы Штифеля (предполагаем, что №1319 вы уже разобрали).
. В общем виде этот вопрос рассматривается в задаче №1319 [4]. Здесь же мы укажем, как найти решения конкретных задач (№№ 1320-1322 [4]). Задачу 1.6 мы решим двумя способами, второй — с помощью схемы Штифеля (предполагаем, что №1319 вы уже разобрали).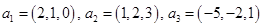 и
и 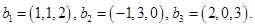
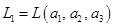 ,
, 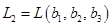 . Будем считать, что координаты векторов заданы в единичном базисе
. Будем считать, что координаты векторов заданы в единичном базисе 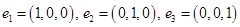 .
.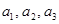 ,
, 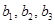 . Его построение сводится к вычислению ранга матрицы, строками которой являются координаты векторов последней системы. Кроме того, базис суммы можно получить, добавляя к базису первого подпространства некоторые из векторов базиса второго подпространства.
. Его построение сводится к вычислению ранга матрицы, строками которой являются координаты векторов последней системы. Кроме того, базис суммы можно получить, добавляя к базису первого подпространства некоторые из векторов базиса второго подпространства.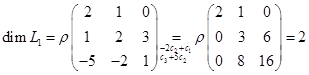 . Базис
. Базис  составляют
составляют 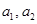 .
.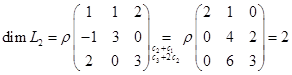 . Базис
. Базис 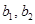 .
.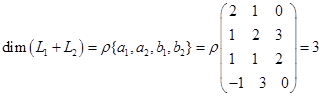 .
.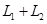 составляют
составляют 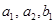 . По формуле (3) получаем
. По формуле (3) получаем 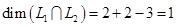 . Базис пересечения будем искать из условия
. Базис пересечения будем искать из условия 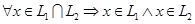 . Значит,
. Значит, 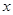 представим в виде
представим в виде 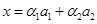 и
и 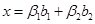 . Приравниваем правые части
. Приравниваем правые части 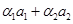
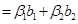 . Это равенство эквивалентно системе трех линейных однородных уравнений с четырьмя неизвестными. Нужно решить эту систему и построить ФСР. Тогда
. Это равенство эквивалентно системе трех линейных однородных уравнений с четырьмя неизвестными. Нужно решить эту систему и построить ФСР. Тогда 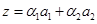
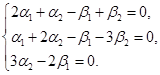
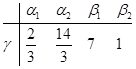
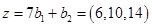 образует базис
образует базис 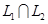 .
.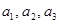 ,
, 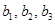 и перебрасываем наверх сначала векторы
и перебрасываем наверх сначала векторы 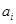 , пока это возможно (квадратиками выделены разрешающие элементы). Векторы
, пока это возможно (квадратиками выделены разрешающие элементы). Векторы 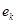 , переходящие налево, не пишем и их координаты не вычисляем.
, переходящие налево, не пишем и их координаты не вычисляем.















