Теоретическая механика:
Центр тяжести

Смотрите также решения задач по нахождению центра тяжести в онлайн решебниках Яблонского (С.8) и Мещерского (§ 9).

Центр тяжести – точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил (Е. М. Никитин, § 42). Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
x_c = (∑ G_ix_i) / ∑ G_i;
(1) y_c = (∑ G_iy_i) / ∑ G_i;
z_c = (∑ G_iz_i) / ∑ G_i.

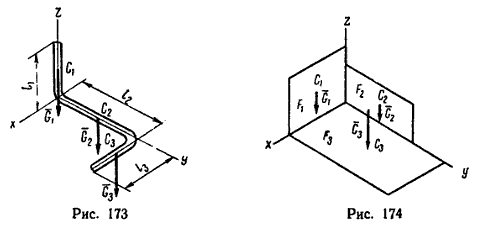
Если тело, центр тяжести которого нужно определить, можно отождествить с фигурой, составленной из линий (например, замкнутый или незамкнутый контур, изготовленный из проволоки, как на рис. 173), то вес G_i каждого отрезка l_i можно представить в виде произведения
G_i = l_id,
где d – постоянный для всей фигуры вес единицы длины материала.

После подстановки в формулы (1) вместо G_i их значений l_id постоянный множитель d в каждом слагаемом числителя и знаменателя можно вынести за скобки (за знак суммы) и сократить. Таким образом, формулы для определения координат центра тяжести фигуры, составленной из отрезков линий , примут вид:
x_c = (∑ l_ix_i) / ∑ l_i;
(2) y_c = (∑ l_iy_i) / ∑ l_i;
z_c = (∑ l_iz_i) / ∑ l_i.

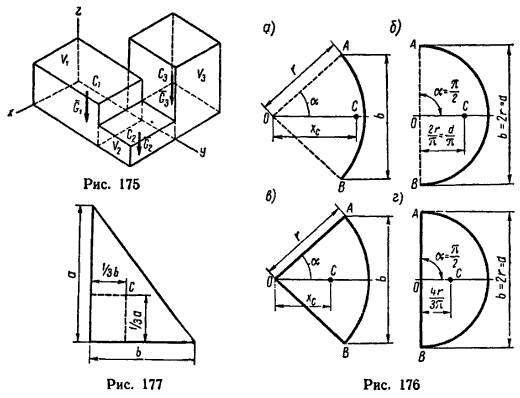
Если тело имеет вид фигуры, составленной из расположенных различным образом плоскостей или кривых поверхностей (рис. 174), то вес каждой плоскости (поверхности) можно представить так:
G_i = F_ip,
где F_i – площади каждой поверхности, а p – вес единицы площади фигуры.

После подстановки этого значения G_i в формулы (1) получаем формулы координат центра тяжести фигуры, составленной из площадей :
x_c = (∑ F_ix_i) / ∑ F_i;
(3) y_c = (∑ F_iy_i) / ∑ F_i;
z_c = (∑ F_iz_i) / ∑ F_i.

Если же однородное тело можно разделить на простые части определенной геометрической формы (рис. 175), то вес каждой части
G_i = V_iγ,
где V_i – объем каждой части, а γ – вес единицы объема тела.

После подстановки значений G_i в формулы (1) получаем формулы для определения координат центра тяжести тела, составленного из однородных объемов :
x_c = (∑ V_ix_i) / ∑ V_i;
(4) y_c = (∑ V_iy_i) / ∑ V_i;
z_c = (∑ V_iz_i) / ∑ V_i.

При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.

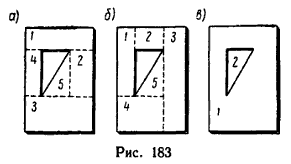
Если известен радиус дуги r и центральный угол 2α, стягиваемый дугой и выраженный в радианах, то положение центра тяжести C (рис. 176, а) относительно центра дуги O определится формулой:
(5) x_c = (r sin α)/α.

Если же задана хорда AB=b дуги, то в формуле (5) можно произвести замену
sin α = b/(2r)
и тогда
(5а) x_c = b/(2α).

В частном случае для полуокружности обе формулы примут вид (рис. 176, б):
(5б) x_c = OC = 2r/π = d/π.

Положение центра тяжести кругового сектора, если задан его радиус r (рис. 176, в), определяется при помощи формулы:
(6) x_c = (2r sin α)/(3α).

Если же задана хорда сектора, то:
(6а) x_c = b/(3α).

В частном случае для полукруга обе последние формулы примут вид (рис. 176, г)
(6б) x_c = OC = 4r/(3π) = 2d/(3π).

Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты.

У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 177).

При решении задач на определение положения центра тяжести любого однородного тела, составленного либо из тонких стержней (линий), либо из пластинок (площадей), либо из объемов, целесообразно придерживаться следующего порядка:

1) выполнить рисунок тела, положение центра тяжести которого нужно определить. Так как все размеры тела обычно известны, при этом следует соблюдать масштаб;

2) разбить тело на составные части (отрезки линий или площади, или объемы), положение центров тяжести которых определяется исходя из размеров тела;

3) определить или длины, или площади, или объемы составных частей;

4) выбрать расположение осей координат;

5) определить координаты центров тяжести составных частей;

6) найденные значения длин или площадей, или объемов отдельных частей, а также координат их центров тяжести подставить в соответствующие формулы и вычислить координаты центра тяжести всего тела;

7) по найденным координатам указать на рисунке положение центра тяжести тела.

Видео:координаты центра тяжести треугольникаСкачать

§ 23. Определение положения центра тяжести тела, составленного из тонких однородных стержней

Видео:Центр тяжести треугольникаСкачать

§ 24. Определение положения центра тяжести фигур, составленных из пластинок

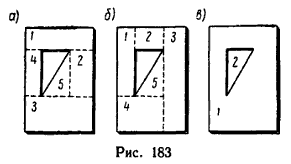
В последней задаче, а также в задачах, приведенных в предыдущем параграфе, расчленение фигур на составные части не вызывает особых затруднений. Но иногда фигура имеет такой вид, который позволяет разделить ее на составные части несколькими способами, например тонкую пластинку прямоугольной формы с треугольным вырезом (рис. 183). При определении положения центра тяжести такой пластинки ее площадь можно разделить на четыре прямоугольника (1, 2, 3 и 4) и один прямоугольный треугольник 5 – несколькими способами. Два варианта показаны на рис. 183, а и б.

Наиболее рациональным является тот способ деления фигуры на составные части, при котором образуется наименьшее их число. Если в фигуре есть вырезы, то их можно также включать в число составных частей фигуры, но площадь вырезанной части считать отрицательной. Поэтому такое деление получило название способа отрицательных площадей.

Пластинка на рис. 183, в делится при помощи этого способа всего на две части: прямоугольник 1 с площадью всей пластинки, как будто она целая, и треугольник 2 с площадью, которую считаем отрицательной.

Видео:Центры тяжести прямоугольных треугольниковСкачать

§ 25. Определение положения центра тяжести сечений, составленных из профилей стандартного проката

При решении задач, приведенных в этом параграфе, нужно пользоваться таблицами из ГОСТа на прокатную сталь: ГОСТ 8509–57, ГОСТ 8510–57, ГОСТ 8239–56, ГОСТ 8240–56.

Эти таблицы для каждого профиля содержат их размеры и площадь, а для уголков и швеллера, кроме того, – координаты центров тяжести.

Видео:Определение центра тяжести сложной фигуры. СопроматСкачать

§ 26. Определение положения центра тяжести тела, составленного из частей, имеющих простую геометрическую форму

Чтобы решать задачи на определение положения центра тяжести тела, составленного из частей, имеющих простую геометрическую форму, необходимо иметь навыки определения координат центра тяжести фигур, составленных из линий или площадей.

Видео:Найдите центр тяжестиСкачать

Как найти центр тяжести?

Опубликовано 21 Окт 2013
Рубрика: Механика | 3 комментария

В инженерной практике случается, что возникает необходимость вычислить координаты центра тяжести сложной плоской фигуры, состоящей из простых элементов, для которых расположение центра тяжести известно. Такая задача является частью задачи определения.

. геометрических характеристик составных поперечных сечений балок и стержней. Часто с подобными вопросами приходится сталкиваться инженерам-конструкторам вырубных штампов при определении координат центра давления, разработчикам схем погрузки различного транспорта при размещении грузов, проектировщикам строительных металлических конструкций при подборе сечений элементов и, конечно, студентам при изучении дисциплин «Теоретическая механика» и «Сопротивление материалов».

Видео:Видеоурок 3. Определение центра тяжести.Скачать

Библиотека элементарных фигур.

Для симметричных плоских фигур центр тяжести совпадает с центром симметрии. К симметричной группе элементарных объектов относятся: круг, прямоугольник (в том числе квадрат), параллелограмм (в том числе ромб), правильный многоугольник.

Из десяти фигур, представленных на рисунке выше, только две являются базовыми. То есть, используя треугольники и сектора кругов, можно скомбинировать почти любую фигуру, имеющую практический интерес. Любые произвольные кривые можно, разбив на участки, заменить дугами окружностей.

Оставшиеся восемь фигур являются самыми распространенными, поэтому они и были включены в эту своеобразную библиотеку. В нашей классификации эти элементы не являются базовыми. Прямоугольник, параллелограмм и трапецию можно составить из двух треугольников. Шестиугольник – это сумма из четырех треугольников. Сегмент круга — это разность сектора круга и треугольника. Кольцевой сектор круга — разность двух секторов. Круг – это сектор круга с углом α=2*π=360˚. Полукруг – это, соответственно, сектор круга с углом α=π=180˚.

Видео:Центр тяжести трапецииСкачать

Расчет в Excel координат центра тяжести составной фигуры.

Передавать и воспринимать информацию, рассматривая пример, всегда легче, чем изучать вопрос на чисто теоретических выкладках. Рассмотрим решение задачи «Как найти центр тяжести?» на примере составной фигуры, изображенной на рисунке, расположенном ниже этого текста.

Составное сечение представляет собой прямоугольник (с размерами a1 =80 мм, b1 =40 мм), к которому слева сверху добавили равнобедренный треугольник (с размером основания a2 =24 мм и высотой h2 =42 мм) и из которого справа сверху вырезали полукруг (с центром в точке с координатами x03 =50 мм и y03 =40 мм, радиусом r3 =26 мм).

В помощь для выполнения расчета привлечем программу MS Excel или программу OOo Calc. Любая из них легко справится с нашей задачей!

В ячейках со светло-желтой заливкой считаем результаты .

Начинаем решение задачи – начинаем поиск координат центра тяжести сечения.

Исходные данные:

1. Названия элементарных фигур, образующих составное сечение впишем соответственно

в ячейку D3: Прямоугольник

в ячейку E3: Треугольник

в ячейку F3: Полукруг

2. Пользуясь представленной в этой статье «Библиотекой элементарных фигур», определим координаты центров тяжести элементов составного сечения xci и yci в мм относительно произвольно выбранных осей 0x и 0y и запишем

в ячейку D4: =80/2=40,000

xc 1 = a 1 /2

в ячейку D5: =40/2=20,000

yc 1 = b 1 /2

в ячейку E4: =24/2=12,000

xc 2 = a 2 /2

в ячейку E5: =40+42/3=54,000

yc 2 = b 1 + h 2 /3

в ячейку F4: =50=50,000

xc 3 = x03

в ячейку F5: =40-4*26/3/ПИ()=28,965

yc 3 = y 03 -4* r3 /3/π

3. Рассчитаем площади элементов F 1 , F 2 , F3 в мм2, воспользовавшись вновь формулами из раздела «Библиотека элементарных фигур»

в ячейке D6: =40*80=3200

в ячейке E6: =24*42/2=504

в ячейке F6: =-ПИ()/2*26^2=-1062

F3 = -π/2* r3 ^2

Площадь третьего элемента – полукруга – отрицательная потому, что это вырез – пустое место!

Расчет координат центра тяжести:

4. Определим общую площадь итоговой фигуры F0 в мм2

в объединенной ячейке D8E8F8: =D6+E6+F6=2642

5. Вычислим статические моменты составной фигуры Sx и Sy в мм3 относительно выбранных осей 0x и 0y

в объединенной ячейке D9E9F9: =D5*D6+E5*E6+F5*F6=60459

в объединенной ячейке D10E10F10: =D4*D6+E4*E6+F4*F6=80955

6. И в завершение рассчитаем координаты центра тяжести составного сечения Xc и Yc в мм в выбранной системе координат 0x — 0y

в объединенной ячейке D11E11F11: =D10/D8=30,640

в объединенной ячейке D12E12F12: =D9/D8=22,883

Задача решена, расчет в Excel выполнен — найдены координаты центра тяжести сечения, составленного при использовании трех простых элементов!

Видео:Центр тяжестиСкачать

Заключение.

Пример в статье был выбран очень простым для того, чтобы легче было разобраться в методологии расчетов центра тяжести сложного сечения. Метод заключается в том, что любую сложную фигуру следует разбить на простые элементы с известными местами расположения центров тяжести и произвести итоговые вычисления для всего сечения.

Если сечение составлено из прокатных профилей – уголков и швеллеров, то их нет необходимости разбивать на прямоугольники и квадраты с вырезанными круговыми «π/2»- секторами. Координаты центров тяжести этих профилей приведены в таблицах ГОСТов, то есть и уголок и швеллер будут в ваших расчетах составных сечений базовыми элементарными элементами (о двутаврах, трубах, прутках и шестигранниках говорить нет смысла – это центрально симметричные сечения).

Расположение осей координат на положение центра тяжести фигуры, конечно, не влияет! Поэтому выбирайте систему координат, упрощающую вам расчеты. Если, например, я развернул бы в нашем примере систему координат на 45˚ по часовой стрелке, то вычисление координат центров тяжести прямоугольника, треугольника и полукруга превратилось бы в еще один отдельный и громоздкий этап расчетов, который «в уме» не выполнишь.

Представленный ниже расчетный файл Excel в данном случае программой не является. Скорее – это набросок калькулятора, алгоритм, шаблон по которому следует в каждом конкретном случае составлять свою последовательность формул для ячеек с яркой желтой заливкой.

Итак, как найти центр тяжести любого сечения вы теперь знаете! Полный расчет всех геометрических характеристик произвольных сложных составных сечений будет рассмотрен в одной из ближайших статей в рубрике «Механика». Следите за новостями на блоге.

Для получения информации о выходе новых статей и для скачивания рабочих файлов программ прошу вас подписаться на анонсы в окне, расположенном в конце статьи или в окне вверху страницы.

После ввода адреса своей электронной почты и нажатия на кнопку «Получать анонсы статей» НЕ ЗАБЫВАЙТЕ ПОДТВЕРЖДАТЬ ПОДПИСКУ кликом по ссылке в письме, которое тут же придет к вам на указанную почту (иногда — в папку «Спам»)!

Несколько слов о бокале, монете и двух вилках, которые изображены на «значке-иллюстрации» в самом начале статьи. Многим из вас, безусловно, знаком этот «трюк», вызывающий восхищенные взгляды детей и непосвященных взрослых. Тема этой статьи – центр тяжести. Именно он и точка опоры, играя с нашим сознанием и опытом, попросту дурачат наш разум!

Центр тяжести системы «вилки+монета» всегда располагается на фиксированном расстоянии по вертикали вниз от края монеты, который в свою очередь является точкой опоры. Это положение устойчивого равновесия! Если покачать вилки, то сразу становится очевидным, что система стремится занять свое прежнее устойчивое положение! Представьте маятник – точка закрепления (=точка опоры монеты на кромку бокала), стержень-ось маятника (=в нашем случае ось виртуальная, так как масса двух вилок разведена в разные стороны пространства) и груз внизу оси (=центр тяжести всей системы «вилки+монета»). Если начать отклонять маятник от вертикали в любую сторону (вперед, назад, налево, направо), то он неизбежно под действием силы тяжести будет возвращаться в исходное устойчивое состояние равновесия (это же самое происходит и с нашими вилками и монетой)!

Кто не понял, но хочет понять – разберитесь самостоятельно. Это ведь очень интересно «доходить» самому! Добавлю, что этот же принцип использования устойчивого равновесия реализован и в игрушке ванька–встань-ка. Только центр тяжести у этой игрушки расположен выше точки опоры, но ниже центра полусферы опорной поверхности.

Всегда рад вашим комментариям, уважаемые читатели.

Прошу, УВАЖАЯ труд автора, скачивать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.

Ссылка на скачивание файла: raschet-tsentra-tyazhesti (xls 17,0KB).

Видео:Практическая №5 Определение центра тяжести сложной фигурыСкачать

Центр тяжести простых геометрических фигур

Центр тяжести составных плоских фигур.

Иногда плоская пластина имеет такой вид, который позволяет разделить ее на составные части несколькими способами, например тонкую пластинку прямоугольной формы с треугольным вырезом (рис. 183). При определении положения центра тяжести такой пластинки ее площадь можно разделить на четыре прямоугольника (1, 2, 3 и 4) и один прямоугольный треугольник 5 – несколькими способами. Два варианта показаны на рис. 183, а и б.

Наиболее рациональным является тот способ деления фигуры на составные части, при котором образуется наименьшее их число. Если в фигуре есть вырезы, то их можно также включать в число составных частей фигуры, но площадь вырезанной части считать отрицательной. Поэтому такое деление получило название способа отрицательных площадей.

Пластинка на рис. 183, в делится при помощи этого способа всего на две части: прямоугольник 1 с площадью всей пластинки, как будто она целая, и треугольник 2 с площадью, которую считаем отрицательной.

Вес отдельной плоской фигуры можно представить так:
G_i = F_ip,
где F_i – площади каждой поверхности, а p – вес единицы площади фигуры, т.е. удельный вес.

После подстановки этого значения G_i в формулы

Центр тяжести простых геометрических фигур

.Центр тяжести – точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
x_c = (∑ G_ix_i) / ∑ G_i;
(1) y_c = (∑ G_iy_i) / ∑ G_i;
z_c = (∑ G_iz_i) / ∑ G_i.

При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.

Если известен радиус дуги r и центральный угол 2α, стягиваемый дугой и выраженный в радианах, то положение центра тяжести C (рис. 176, а) относительно центра дуги O определится формулой:
(5) x_c = (r sin α)/α.

Если же задана хорда AB=b дуги, то в формуле (5) можно произвести замену
sin α = b/(2r)
и тогда
(5а) x_c = b/(2α).

В частном случае для полуокружности обе формулы примут вид (рис. 176, б):
(5б) x_c = OC = 2r/π = d/π.

Положение центра тяжести кругового сектора, если задан его радиус r (рис. 176, в), определяется при помощи формулы:
(6) x_c = (2r sin α)/(3α).

Если же задана хорда сектора, то:
(6а) x_c = b/(3α).

В частном случае для полукруга обе последние формулы примут вид (рис. 176, г)
(6б) x_c = OC = 4r/(3π) = 2d/(3π).

Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты. У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 177).

10.Главные оси и главные центральные мом. инерции.

Оси, проходящие через центр тяжести сечения, называют центральными.Если фигура имеет ось симметрии, то последняя всегда проходит через центр тяжести фигуры, т. е. оси симметрии одновременно являются и центральными осями.Если элементарные площадки, выделенные в пределах рассматриваемого сечения, будем умножать на квадраты расстояний до оси, то получим осевые моменты инерции площадок. Суммируя моменты инерции всех площадок, найдем осевые моменты фигуры в целом:

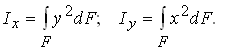Составляя интеграл, в котором подынтегральное выражение представляет собой произведение элемента площади на квадрат расстояния до начала координат (рис. 9.17), получим полярный момент инерции:

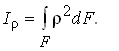Рис. 9.17. Схема к определению моментов инерции и моментов сопротивления.

Отметим еще одну характеристику, в которой площадка dF умножается на произведение координат

Эту величину называют центробежным моментом инерции. Приведенные моменты инерции измеряются в единицах длины» взятой в четвертой степени ( , ).
Осевые и полярные моменты инерции фигуры — величины положительные и не могут быть равными нулю. Центробежный момент инерции в зависимости от положения осей может быть положительным или отрицательным, а также равным нулю. Две взаимно перпендикулярные оси, относительно которых центробежный момент инерции равен нулю, называют главными осями инерции и обозначаются . Для симметричной фигуры ось симметрии является и главной осью.
Осевые моменты инерции, определенные относительно главных осей, имеют максимальное и минимальное значения. Момент инерции сложной фигуры равен сумме моментов инерции образующих ее фигур. Подчеркнем, что сказанное справедливо в том случае, когда все моменты инерции вычисляются относительно одной и той же оси.
Для моментов инерции существует еще одно правило, часто используемое в расчетах. Применительно к осевым моментам оно «формулируется следующим образом: момент инерции фигуры относительно оси, параллельной центральной, равен моменту инерции относительно центральной оси плюс произведение площади фигуры, на квадрат расстояния между осями (рис. 9.18):

Рис. 9.18. Схема к определению моментов инерции относительно разных осей координат.

Для центробежных моментов инерции соответствующее правило в аналитическом виде выглядит так:

🎬 Видео

97 Медианы и центр тяжести треугольникаСкачать

Определение центра тяжести сложных сечений. Фигуры из ГОСТ.Скачать

Центр тяжести. ЭкспериментСкачать

Урок 79. Центр масс тела и методы определения его положенияСкачать

Найти центр кругаСкачать

Определение центра тяжести плоской фигуры. Подробное объяснение. Сопромат для чайниковСкачать

Определение центра тяжестиСкачать

Как найти центр тяжести любой фигуры?Скачать

Центр тяжести Метод дополненияСкачать

Центр тяжести тела. Условия равновесия тел | Физика 7 класс #46 | ИнфоурокСкачать

Центр массСкачать