2. Плоская система сил.
2.2 Главный вектор и главный момент плоской системы сил.
Приведение к простейшему виду.
2.2.1. Определить главный вектор плоской системы сил, если заданы его проекции на координатные оси Rx = 300Н, Rу = 400Н. (Ответ 500)
2.2.2. Определить главный момент системы двух сил относительно точки А, если силы G = 1Н, F = 5Н, расстояние l = 0,2 м, угол φ = 60°. (Ответ -0,916)
2.2.3. К вершинам квадрата приложены четыре силы F1 = F2 = F3 = F4 = 1Н. Определить модуль равнодействующей этой системы сил. (Ответ 2,0)
2.2.4. За центр приведения данной системы сил выбрана точка, расположенная на оси Оу, в которой главный момент равен нулю. Определить ординату этой точки, если силы
F1 = F2 = F3 = 1Н, F4 = 2Н, радиус r = 1 м. (Ответ -1,0)
2.2.5. К вершинам равностороннего треугольника приложены силы F1 = F2 = F3 = 1Н.
Определить модуль равнодействующей этой системы сил. (Ответ 1,0)
2.2.6. Заданы силы F1 = F2 = F3 = 12H, F4 = 14Н. Определить главный момент заданной плоской системы сил относительно точки О, если радиус r = 0,2 м. (Ответ 0,233)
2.2.7. К вершинам прямоугольного треугольника приложены три силы.
Определить значение угла α в градусах, при котором главный момент данной системы си л
М 0 = -2 кН•м, если сила F2=4 кН, расстояние l = 1 м. (Ответ 30,0)
2.2.8. К вершинам прямоугольного треугольника приложены силы F1 = 3Н, F2 = 6Н, F3 = 14Н. Определить значение угла а в градусах, при котором главный вектор данной системы сил параллелен оси Ох (Ответ 30,0)
2.2.9. К прямоугольнику приложены четыре силы по 10Н каждая. Определить модуль главного вектора заданной системы сил, если угол α = 60°. (Ответ 22,4)
2.2.10. К квадрату приложены шесть сил по 6Н каждая. Определить главный момент заданной плоской системы сил относительно точки А, если расстояние l = 0,5 м. (Ответ 8,48)
2.2.11. К вершинам квадрата приложены шесть сил по 4Н каждая. Определить главный момент заданной плоской системы сил относительно точки B, если расстояние l = 0,4 м. (Ответ 4,99)
2.2.12. К вершинам прямоугольного треугольника приложены силы F1 = 12Н, F2 = 4Н, F3 = 2Н. Определить значение угла α в градусах, при котором главный вектор данной системы сил параллелен оси Оу. (Ответ 60,0)
2.2.13. К прямоугольнику приложены силы F1 = 4Н, F2 = 5Н, F3 = 8Н, F4 = 2Н. Определить главный момент заданной системы сил относительно точки А, если расстояние l = 1 м, угол α = 30°. (Ответ 6,89)
2.2.14. К правильному шестиугольнику приложены пять равных по модулю сил. Определить в градусах угол между главным вектором этой системы сил и осью Ох. (Ответ 180)
2.2.15. Задана плоская система сил F1 = F2 = F3 = 2H, F4 = 10Н. Определить главный момент лой системы сил относительно точки А, если радиус r = 1 м. (Ответ 11,3)
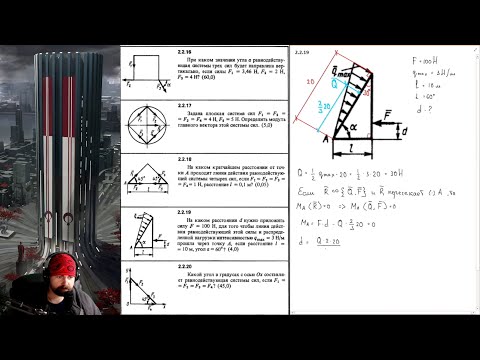
2.2.16. При каком значении угла α равнодействующая системы трех сил будет направлена вертикально, если силы F1 = 3,46Н, F2 = 2Н, F3 = 4Н? (Ответ 60,0)
2.2.17. Задана плоская система сил F1 = F2 = F3= F4 = 4Н, F5 = 5Н. Определить модуль главного вектора этой системы сил. (Ответ 5,0)
2.2.18. На каком кратчайшем расстоянии oт точки А проходит линия действия равнодействующей системы четырех сил, если F1 = F2 =F3 = F4 = 1H, расстояние l = 0,1 м? (Ответ 0.05)
2.2.19. На каком расстоянии d нужно приложить силу F = 100Н, для того чтобы линия
действия равнодействующей этой силы и распределенной нагрузки интенсивностью
qmax = 3 Н/м прошла через точку А, если расстояние l = 10м, угол α = 60°? (Ответ 4,0)
2.2.20. Какой угол в градусах с осью Ох составляет равнодействующая системы сил,
если F1 = F2 = F3 = F4? (Ответ 45,0)
2.2.21. К квадрату приложена система четырех сил, причем силы F1 = F2 = F3 = 1Н.
Определить модуль силы F4, при которой равнодействующая системы R = 2Н. (Ответ 1,0)
- Тема 1.4. Плоская система произвольно расположенных сил
- Задание на расчетно-графическую работу №2. Фрагмент методички с заданиями, которые задают где-то на Дальнем Востоке. Задания не являются оригинальными и взяты из другой методички. Образцы оформления здесь
- Гарантии (в плюсиках тоже есть текст)
- 💡 Видео
Видео:2.2. Главный вектор и главный момент плоской системы сил. Приведение к простейшему видуСкачать
Тема 1.4. Плоская система произвольно расположенных сил
Знатьтеорему Пуансо о приведении силы к точке.
Уметь приводить произвольную плоскую систему сил к точке, определяя величины главного вектора и главного момента системы.
Знатьтри формы уравнений равновесия и уметь ими пользоваться при определении реакций в опорах балочных систем.
Основные формулы и предпосылки расчета.
Виды опор балок и их реакции (рис. П2.1)
Моменты пары сил и силы относительно точки (рис. П 2.2)
Главный вектор
Главный момент
Условия равновесия
Упражнения при подготовке к самостоятельной работе
1. Перенести силу F в точку А, используя теорему Пуансо (рис. П2.3).
F = 20кН; АВ = 6м; ВС = 2м.
2. Система сил находится в равновесии. Определить величину момента пары m (рис. П2.5).
3. Нанести реакции в опорах балок 1 и 2 (рис. П2.6).
4. Определить величину реакции в опоре А. Приложена распределенная нагрузка интенсивностью q = 5 кH/м (рис. П2.7).
Определение величин реакции в опорах балочных систем под действием сосредоточенных и распределенных нагрузок
Задание 3. Определить величины реакций в шарнирных опорах балки. Провести проверку правильности решения.
 |  |
 |  |
 |  |
| Параметр | Варианты | ||||||||||||||
 F, кН F, кН | |||||||||||||||
 q, кН/м q, кН/м | |||||||||||||||
| м, кНм | |||||||||||||||
| а, м. | |||||||||||||||
| Рис. | а | б | в | г | д | е | е | е | в | д | б | д | б | б | в |
| Параметр | Варианты | ||||||||||||||
 F, кН F, кН | |||||||||||||||
 q, кН/м q, кН/м | |||||||||||||||
| м, кНм | |||||||||||||||
| а, м. | |||||||||||||||
| Рис. | а | б | в | г | д | е | е | е | в | д | б | д | б | б | в |
ТЕСТ ДЛЯ САМОКОНТРОЛЯ:
ТЕМА: 1.4. Статика
Произвольная плоская система сил.
| Вопросы | Ответы | Код |
1. Найти главный вектор системы сил, если:  Fl = 2кН, F2 = 3кН, F3 = 5кН, F4=Fs=8KH; диаметр колеса 0,8 м. Fl = 2кН, F2 = 3кН, F3 = 5кН, F4=Fs=8KH; диаметр колеса 0,8 м. | 5кН | |
| l1KH | ||
| 12кН | ||
| 16кН | ||
2. Найдите главный момент системы. Центр приведения находится в точке С.  | 49,14кН·м | |
| 52,32 кН·м | ||
| 54,14кH·M | ||
| 64,14кН·м | ||
3. Приводится уравнение равновесия, для определения реакции в опоре А. Определите, какого члена уравнения не хватает: RyA ·8 + Fl·5 — m + F3·1 + . = 0.  | F2 cos60˚ | |
| F2 cos30˚ | ||
| - F2 sin60˚ | ||
| -F2 ·2 sin60˚ | ||
4. Найти главный вектор системы сил.  | 2 кН | |
| 4 кН | ||
| 6 кН | ||
| 8 кН |
Тема 1.6. Центр тяжести.
Знать методы определения Центра тяжести тела и плоских сечении, формулы для определения положения ЦТ плоских сечении.
Уметь определять положение Центра тяжести сложных геометрических фигур, определять положение Центра тяжести фигур, составленных из стандартных профилей.
Основные формулы и предпосылки расчета
Центры тяжести простейших сечении (рис. П3.1)
Геометрические характеристики стандартных прокатных профилей в задачниках или учебниках по «Технической механике».
Методы расчета:
1) метод симметрии;
2) метод разделения на простые части;
3) метод отрицательных площадей.
Координаты центров тяжести сложных и составных сечений:
где Ak — площади частей сечения; Xk; Yk — координаты ЦТ частей сечения; А — суммарная площаль сечения,
Видео:Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

Задание на расчетно-графическую работу №2. Фрагмент методички с заданиями, которые задают где-то на Дальнем Востоке. Задания не являются оригинальными и взяты из другой методички. Образцы оформления здесь
Задача 1. Пример
Для балок построить эпюры поперечных сил и изгибающих моментов. Данные для задачи своего варианта взять из таблицы 5
Задача 2. Пример
Определить аналитическим способ усиления в стержнях АВ и ВС заданной стержневой системы (рис. 2). Исходные данные для задачи своего варианта взять из таблицы 2
Задача 3. Пример
Определить реакции опор балки нагруженной как показано на схеме (рис. 5). Исходные данные приведены в таблице 3
Задача 3. Схемы. Пример
Определить реакции опор балки нагруженной как показано на схеме (рис. 5). Исходные данные приведены в таблице 3
Задача 4. Пример
Определить положение центра тяжести сложной фигуры, ее сечение имеет вид (см. рис. 8). Данные для задачи своего варианта взять из таблицы 4
Задание №18. Пример
1. Определить положение расчетного центра тяжести фигуры, размеры указаны в мм.
2. Вырезать фигуру из плотной бумаги.
3. Методом подвешивания определить опытное положение центра тяжести.
4. Сравнить полученные результаты
4.4. Пример
Чему равно наибольшее касательное напряжение в толстой части ступенчатого вала, если в тонкой части оно 135 МПа?
Ответ: τmax2=80 МПа
10. Поезд весом 3000 кН идет со скоростью 36 км/ч. Сила сопротивления движению составляет 0,005 веса поезда. Определить полезную мощность тепловоза. Движение прямолинейное по горизонтальному пути
Вариант 5 Пример
Определить проекцию равнодействующей системы сил на ось 0у F1=10 кН F2=8 кН F =20 кН
Как направлен вектор равнодействующей силы, если известны величины его проекции? 11Н 23,59 Н Определить αx
Какой вектор силового многоугольника является равнодействующей силой?
Груз F находится в равновесии. Указать, какой из силовых треугольников для шарнира В построен верно.
Груз F находится в равновесии. Указать, какие условия для точки равновесия В записаны верно
5.4.7 Пример
В центре приведения О главный вектор R=5 Н и главный момент МO=25 Нм. Определить значение главного момента в центре приведенияя А, если ОА=1 м
5.4.8 Пример
При приведении системы сил к центру О получены главный вектор R=10 Н и главный момент М0=20 Нм. Определить модуль главного момента в центре приведения А, если расстояние ОА=2 м
ЗАДАЧА №12. Пример
Стержень AB длиной 60 см скользит своими концами и по сторонам угла. Определить скорости точек В и С, а также угловую скорость стержня, если скорость точки А равна 10 см/с
ЗАДАЧА 8. Пример
Для изображенной на схеме передачи определить вращающий момент Т2 на ведомом валу. Исходные данные: мощность на ведущем валу Р1=8 кВт; угловая скорость ведущего вала ω1=40 рад/с; коэффициент полезного действия передачи η=0,97; передаточное число передачи u=4
Промежуточная контрольная работа по Технической механике. Вариант 10. Пример
• Задание №1. Груз подвешен на стержнях и находится в равновесии. Определить усилия в стержнях.
• Задание №2. Груз подвешен на стержнях и канатах находится в равновесии. Определить усилия в стержнях.
• Задание №3. Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом
ВАРИАНТ 6. Задача 1 Пример
Определить реакции стержней кронштейна АВС, изображенного на схеме (рис.5), если сила F направлена вертикально вниз.
Стержни АВ и ВС считать жесткими, невесомыми. Точки А, В, С — цилиндрические шарниры.
Значение силы F, углы α, β сведены в таблице
2. Пример
В соединениях 1 и 2 кронштейн закреплен на колонне болтами, установленными в отверстиях с зазором. Какой из вариантов, при прочих равных условиях, рациональнее, если в качестве критерия рациональности принять нагрузочную способность
Задание 3.
К тормозному колесу диаметром 370 мм, жестко посаженному на вал двигателя, прижимают с помощью рычага тормозную колодку силой F=180 Н.
Вал вращается при этом равномерно и делает 1950 об/мин.
Коэффициент трения между колесом и колодкой 035. Опрсдедкть мощность (в кВт и л.с.) развиваемую двигателем, если потери на трение и нем составляют 15%
Колесный трактор имеет двигатель, развивающий максимальную Мощность 62.5 кВт КПД трансмиссии трактора 0.72 масса трактора вместе с перевозимым грузом 2250 кг.
Определить наибольшую скорость движения в км/ч, с которой может двигаться трактор по асфальтированной дороге, коэффициент трения равен 0.18
КОНТРОЛЬНАЯ РАБОТА № 1. Вариант 3
Задача 1. Пример Определить реакции стержней, удерживающих грузы F1 и F2 . Массой стержней пренебречь. F1=0,6 кН F2=0,4 кН
Задача 2. Пример Определить реакции опор двухопорной балки. q=10 Н/м F=16 Н М=14 Нм
Задача 3. Пример Определить центр тяжести плоской фигуры
Задача 4. Пример Скорость самолёта при отрыве от взлётной полосы должна быть 300 км/ч. Определить минимальную длину взлётной полосы, необходимую для того, чтобы лётчик при разгоне испытывал перегрузку, не превышающую его утроенный вес.
Задача 5. Пример Определить реакции опор балки. F=18 Н q=2 Н/м
Вариант 1 Пример
1. Определить проекции силы F=14 Н на оси координат.
2. Определить моменты сил относительно указанной точки. Дано: F1=25 Н, F2=14 Н, F3=28 Н, а=20 см, b=50 см.
3. Чему равено модуль силы Р, если её проекции Px=9 Н, Py=-12 Н.
4. Найти моменты сил относительно осей
Тест l-го уровня. Сдвиг, срез, смятие Пример
Во всех заданиях выбрать номер правильною ответа
Задание 1. Если в поперечных сечениях элемента возникает, внутренний силовой фактор — поперечная сила, то такой вид деформации называется: растяжением сдвигом смятием
Задание 2. Поперечная сила действует: в плоскости поперечного сечения бруса перпендикулярно плоскости поперечного сечения бруса вдоль продольной оси бруса
Задание 3. Единица измерения напряжения 1 Па составляет: Н/мм 2 кг/см 2 Н/м 2 (модуль сдвига)
Тест l-го уровня. Сдвиг, срез, смятие Пример
Задание 4. Болт нагружен растягивающей силой F. Рассчитать величину площади смятия, если d=20 мм, h=14 мм, D=36 мм 468 224 1331 703 мм 2
Задание 5. Из условия прочности болта на смятие определить величину допускаемой нагрузки F, если [τср.]=100 МПа, [σсм]=240 МПа, используя данные задания 4 22,4 кН 84.3 кН 168,7 кН 70,3 кН
Задание 6. Установить соответствие в формуле зависимости между тремя упругими постоянными материала: G = E/2(1-μ) Коэффициент Пуассона Модулем упругости 1-го рода Модулем упругости 2-го рода (модуль сдвига)
Тест. Эпюры балок. Очертания контуров эпюр Пример
Указать соответствие между схемой балки и эпюрами Q и М. Схема ответа
Тест. Эпюры простых балок
Установить соответствие между схемой балки и эпюрами поперечных сил Q и изгибающих моментов М. Схема ответа Q — а) М — б)
Гарантии (в плюсиках тоже есть текст)
Посмотрите на мой сайт. Все виды связи, почта и группа 
Клиент, довольный работой, возвращается еще, приводит друга, заказывает для товарища. Причем чем быстрее он получит качественную работу, тем выше вероятность повторного заказа. Это правило проверено многолетней практикой. Не сомневайтесь. Мой бизнес строится на репутации.
💡 Видео
определение реакций в стержнях от действия грузовСкачать

Видеоурок 1. Определение реакций жёстких стержней.Скачать

Система сходящихся силСкачать
5.3. Главный момент произвольной пространственной системы силСкачать

Система сходящихся сил. Решение задач по МещерскомуСкачать

Произвольная плоская система сил. Задача 1Скачать

Приведение системы сил к простейшему видуСкачать

§4.3. Главный вектор и главный момент сил инерцииСкачать

Практика_№7_Равновесие_пространственной_системы_сил_2_часаСкачать

3.2. Равновесие статически определимой системы тел под действием плоской системы сил (2 из 3)Скачать

2.4. Равновесие произвольной плоской системы сил (1 из 4)Скачать

2.4. Равновесие произвольной плоской системы сил (3 из 4)Скачать

Определение реакций опор в балке. Сопромат.Скачать

Теоретическая механика. Нахождение реакций связей на при плоской системе сил. Задача 1, часть 1Скачать

Термех. Статика. Расчётно-графическая работа по статике №2. Задание 1 и решениеСкачать

Определение реакций опор простой рамыСкачать

Термех. Статика. Равновесие плоской произвольной системы силСкачать

1.2. Равновесие плоской системы сходящихся сил (1 из 2)Скачать



































