Видео:Координаты вектора в пространстве. 11 класс.Скачать
ABCDA1B1C1D1 — параллелепипед, М — точка пересечения DC1 и –D1C, (АВ) ⃗ = a ⃗, (AD) ⃗ = Ь ⃗, (АА1) ⃗ = с ⃗. Разложите вектор (AM)
Видео:№786. Отрезки AA1, ВВ1 и СС1 — медианы треугольника ABC. Выразите векторы AA1, BB1, СС1Скачать
Ваш ответ
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать
решение вопроса
Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,921
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:№364. Точка К—середина ребра В1С1 куба ABCDA1B1C1D1. Разложите вектор АК по векторам а = АВ,Скачать
Смешанное, векторное и скалярное произведение векторов
Задача:
Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).
Найти:
Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5). Решение:
- а) Объем параллелепипеда будем искать через смешанное произведение векторов (AB AD AA1). Мы знаем, что модуль смешанного произведения векторов равен объему параллелепипеда, построенному на этих векторах.
| (AB AD AA1) | = |
| = | 20 — 18 + 0 — 0 — 30 + 16 | = | -12 | . |
|---|
Мы нашли смешанное произведение, ещё надо его взять по модулю и найдём объем параллелепипеда:
VABCDA1B1C1D1=12.
б) Площадь, как мы уже знаем, можно искать через векторное произведение векторов. Грань ABCD построена на векторах AB и AD, найдём их векторное произведение. SABCD= |[AB AD]|.
| [AB AD] | = |
| = | 6i — 8j — 2k | , |
|---|
Теперь найдём модуль этого вектора:
| SABCD= |[AB AD]|=√ | (36+64+4) | =2√(26). |
|---|
| [AD AA1] | = |
| = | 9i — 16j — k | , |
|---|
SADD1A1= |[AD AA1]|=√(81+256+1)=13√2.
| h | = |
| = |
| = |
| = |
| . |
|---|
| cos(λ1) | = |
| . |
|---|
Координаты вектора AB мы имеем, от вектор B1D надо найти. Для этого используем следующую формулу:
B1D = B1A1 + A1A + AD = — AB — AA1 + AD1 = — (4, 3, 0) — (-3, -2, 5) + (2, 1, 2); (Не забывайте, что всё это векторы, надо сложить их соответствующие координаты. )
Сделав вычисления по этой формуле, мы найдём, что вектор B1D имеет координаты (1, 0, -3). Теперь надо найти длину векторов AB и B1D:
|AB|=√(16+9+0)=5, |B1D|=√(1+0+9)=√(10).
Найдём скалярное произведение векторов AB и B1D, (AB B1D)=4*1 + 3*0 + 0*(-3)=4.
Теперь, имея все данные мы можем подставить их в нашу формулу:
| cos(λ1) | = |
| = |
| . |
|---|
д) Что бы найти cos(λ2), мы используем то, что угол между двумя плоскостями равен углу между перпендикулярами до этих плоскостей. А как мы знаем, векторное произведение — это и есть перпендикуляр до плоскости перемножаемых векторов. Поэтому в роле перпендикуляра к плоскости ADD1A1 мы можем взять вектор [AD AA1], который мы нашли в пункте б), и знаем, что его координаты (9, -16, -1), точно также и для плоскости ABCD — вектор [AB AD] с координатами (6, -8, -2).
Теперь нам остаётся, как в предыдущем варианте найти только косинус угла между двумя векторами, координаты которых нам известны.
| cos(λ2) | = |
| = |
| . |
|---|
Вот таким не хитрым способом мы и нашли косинус угла между гранями ABCD и ADD1A1.
Видео:№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать
Найдите вектор ав аа1 с1в1
4.6. Задачи с решениями
1. В параллелепипеде обозначим . Выразить через векторы a, b, с диагонали параллелепипеда и диагонали граней.
Решение. Сделаем чертёж. Пользуясь правилом сложения векторов, получаем:
AC = AB + AD = b + с, AC1 = AA1 + AC = a + b + с .
Из того же треугольника AA1C получаем: A1C = AC — AA1 = b + с — a.
Чтобы найти B1C, заметим, что B1C = A1D, так как у этих векторов совпадают и длины, и направления. Поэтому B1C = A1D = AD — AA1 = с — a.
Аналогично: DC1 = AB1 = AA1 + AB = a + b .
2. Найти длину и направляющие косинусы вектора AB, если его начало и конец находятся в точках A(7, 6), B(2 — 6).
Решение. Так как каждая точка задана двумя координатами, то рассматривается вектор на плоскости. Находим его координаты, вычитая из координат точки B (конца вектора) координаты точки A (начала вектора): AB = (2 — 7, —6 — 6) = (—5, —12). Находим длину: |AB | = 13, направляющие косинусы: .
3. Найти координату z вектора a = (1, —3, z), если известно, что она отрицательна, а модуль |a| = . Где окажется конец вектора a, если его отложить из точки M(5, —2, 1)?
Решение. По условию, . поэтому ZN = —8.
4. Найти расстояние между точками A(5, —2, 4) и B( —1, 0, 6).
Решение. Расстояние равно длине вектора AB. Найдём:
5. При каких p, q векторы a = (2,p, — 1), b = qi + 9j + 3k будут коллинеарными?
🌟 Видео
№330. Нарисуйте параллелепипед ABCDA1B1C1D1 и обозначьте векторы C1D1, BA1Скачать
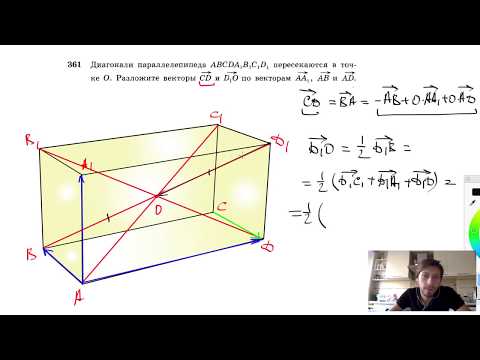
№361. Диагонали параллелепипеда ABCDA1B1C1D1 пересекаются в точке О. Разложите векторыСкачать
№359. Дан параллелепипед ABCDA1B1C1D1. а) Разложите вектор BD1 по векторам ВА, ВС и ВВ1.Скачать
Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать
№336. Даны точки A, В, С и D. Представьте вектор АВ в виде алгебраической суммы следующихСкачать
18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать
Единичный векторСкачать
№327. На рисунке 97 изображен параллелепипед ABCDA1B1C1D1. Назовите вектор, нСкачать
Как находить угол между векторамиСкачать
8 класс, 40 урок, Понятие вектораСкачать
ЗАДАЧА - ЧУДО! Победи мастера, найди угол альфа!Скачать
1. Векторы и параллелограмм задачи №1Скачать
№934. Найдите координаты вектора АВ, зная координаты его начала и конца: а) А (2; 7), B (-2; 7);Скачать
