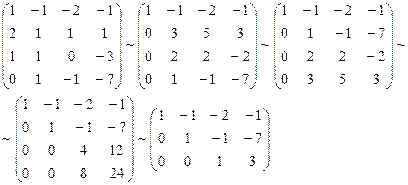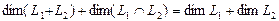Найдите размерность линейной оболочки данных четырех векторов (2 видео)

Линейные оболочки и подпространства

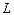
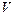
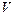
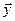
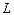
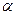
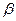
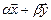
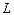
Определение. Подпространством линейного пространства называется множество векторов из такое, что для любых двух векторови из и любых двух вещественных чисел и линейная комбинация также принадлежит .

Утверждение. Подпространство само является линейным пространством.

Определение. Линейной оболочкой системы векторов называется множество всех линейных комбинаций векторов . Обозначается .

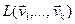
Утверждение. Линейная оболочка системы векторов является подпространством.

Определение. Пересечением двух подпространств и называется множество всех векторов, принадлежащих одновременно и ,и . Обозначается .

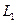
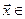
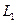
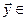
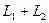
Определение. Суммой двух подпространств и называется множество всех векторов , представимых в виде , где , . Обозначается .

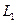
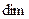
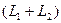
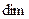
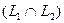
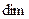
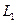
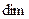
Утверждение. Сумма и пересечение подпространств и являются линейными пространствами, и их размерности связаны равенством

+ = + .

Определение. Сумма двух подпространств называется прямой суммой, если пересечение этих подпространств состоит только из нулевого вектора.

Примеры

1. Найти размерность и какой-нибудь базис суммы и пересечения подпространств, порождённых векторами .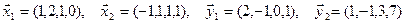

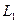
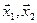
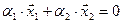
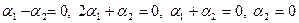
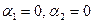
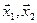
Решение. Вычислим вначале размерность подпространств. С этой целью установим, являются ли линейно независимыми векторы, порождающие данные подпространства. Для подпространства , порождённого векторами , равенство нулю линейной комбинации , эквивалентное системе уравнений , достигается лишь при условии . Следовательно, векторы линейно

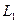
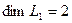
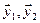
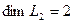
независимы и размерность подпространства равна 2: . Для подпространства , порождённого векторами , проводя аналогичный анализ, получим .

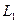
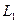
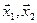
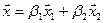
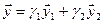
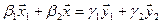
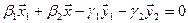
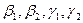
Вычислим теперь размерность пересечения подпространств и . По определению векторы, составляющие пересечение, принадлежат одновременно обоим подпространствам. Произвольный вектор подпространства является линейной комбинацией базисных векторов : . Аналогично для подпространства имеем , тогда условие принадлежности пересечению есть или .

Это условие представляет собой систему уравнений относительно коэффициентов . Составим матрицу системы и упростим её с помощью элементарных преобразований:

Как видно ранг системы равен 3. Значит ФСР состоит из одного линейно независимого вектора. Найдём его, решив систему уравнений, соответствующих последней матрице, получим ,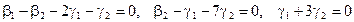

откуда .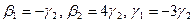

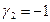
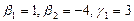
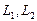
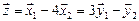
Полагая свободное неизвестное , для остальных имеем

. Итак, пересечение подпространств имеет один базисный вектор

Размерность пересечения 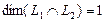. Следовательно, в соответствии с равенством

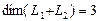
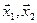
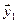
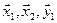
размерность суммы подпространств . В качестве базиса суммы подпространств можно взять, например, векторы , дополненные вектором . В линейной независимости векторов убедиться нетрудно.

Задачи

3.39. Найти размерность и какой-нибудь базис подпространства, порожденного векторами , , , , .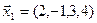

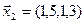
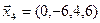
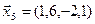
3.40. Найти размерность и какой-либо базис линейной оболочки векторов , , , , .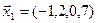

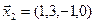
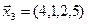
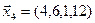
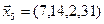
3.41. Является ли подпространством в указанном пространстве множество

а) векторов, выходящих из начала координат и заканчивающихся на фиксированной прямой, в пространстве R 2 ;

б) бесконечно малых числовых последовательностей в пространстве сходящихся последовательностей;

в) сходящихся к числу последовательностей в пространстве сходящихся последовательностей;

г) диагональных матриц в пространстве квадратных матриц того же порядка;

д) невырожденных матриц в пространстве симметричных матриц того же порядка;

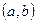
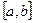
е) дифференцируемых на интервале функций в пространстве функций, непрерывных на отрезке .

3.42. Почему не является подпространством в указанном пространстве множество

а) векторов, каждый из которых лежит на одной из координатных плоскостей, в пространстве R 3 ;

б) векторов из пространства R n , координаты которых удовлетворяют уравнению ;

в) расходящихся числовых последовательностей в пространстве ограниченных последовательностей;

г) вырожденных матриц в пространстве квадратных матриц того же порядка;

д) монотонно возрастающих и ограниченных на множестве 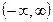функций в пространстве функций, ограниченных на том же множестве.

3.43. Найти размерность и какой-либо базис подпространства решений однородной системы:

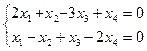
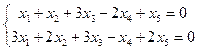
а) ; б) ;

в) .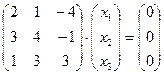

3.44. Доказать, что данное множество является подпространством в R n , найти его размерность и какой-либо базис:

а) все n-мерные векторы, координаты которых удовлетворяют уравнению ;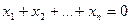

б) все n-мерные векторы, у которых первая координата равна нулю;

в) все n-мерные векторы, у которых первая и последняя координаты равны между собой;

г) все n-мерные векторы, у которых координаты с четными номерами равны нулю;

д) все n-мерные векторы, у которых координаты с нечетными номерами равны между собой.

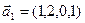
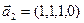
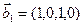
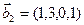
3.45. Найти размерность суммы и пересечения подпространств, порожденных векторами , и , . Является ли эта сумма прямой суммой?

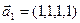
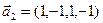
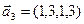
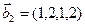
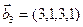
3.46. Найти размерность суммы и пересечения линейных оболочек векторов , , и , , . Является ли их cумма прямой?

3.47. Найти базис суммы и пересечения двух подпространств, порожденных соответственно векторами и , если

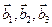
а) , , , , , ;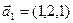

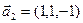
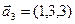
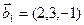
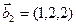
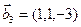
б) , , , , , .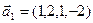

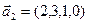
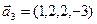
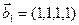
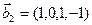
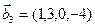
3.48. Найти базис суммы и пересечения линейных оболочек и , если

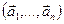
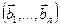
а) , , , ;

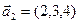
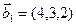
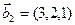
б) , , , , , .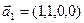

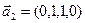
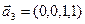
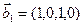
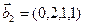
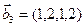
Является ли прямой сумма этих подпространств?

Содержание

Линейная алгебра Лабораторные работы 8 -13 (стр. 1 )
Лабораторная работа 8
ЛИНЕЙНОЕ ПРОСТРАНСТВО. ПОДПРОСТРАНСТВО.
БАЗИС И РАЗМЕРНОСТЬ
Лабораторная работа 9
МАТРИЦА ПЕРЕХОДА. КООРДИНАТЫ ВЕКТОРОВ
🎥 Видео

Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

Линейная алгебра Лабораторные работы 8 -13 (стр. 1 )

Найдите размерность линейной оболочки данных четырех векторов

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОУ ВПО «Пермский государственный университет»

Кафедра дискретной математики
и информатики

Лабораторные работы 8 -13

Линейная алгебра: лабораторные работы 8-13 / сост. , , ; Перм. ун-т.– Пермь, 2006. – 39 с.

Приводится 13-14 вариантов лабораторных работ по шести темам курса линейной алгебры. Для проверки готовности перед каждой работой предложены вопросы для самоконтроля. Тексты лабораторных работ могут быть использованы также в качестве индивидуальных заданий.

Лабораторные работы предназначены для студентов всех специальностей механико-математического факультета.

Печатается по решению методической комиссии механико-математического факультета Пермского университета.

L(a1,…,as) – линейная оболочка системы векторов а1,…аs.

An – n-мерное пространство векторов-строк (арифметическое пространство).

Mn – пространство матриц n-го порядка.

Pn – пространство многочленов степени не выше n.

V3 – пространство трехмерных векторов-отрезков.

– прямая сумма.

Видео:Линейная зависимость и линейная независимость векторов.Скачать

Лабораторная работа 8

Видео:Линейная оболочка. Базис и размерностьСкачать

ЛИНЕЙНОЕ ПРОСТРАНСТВО. ПОДПРОСТРАНСТВО.

Видео:Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

БАЗИС И РАЗМЕРНОСТЬ

Вопросы для самоконтроля:

1.Какое множество называется линейным пространством?

2.Какие операции определены в линейном пространстве?

3.Что такое подпространство?

4.Выполнение каких условий достаточно проверить для того, чтобы убедиться, что некоторое подмножество линейного пространства является его подпространством?

5.Что называется линейной оболочкой конечной системы векторов?

6.Что такое базис линейного пространства?

7.Что такое размерность линейного пространства?

8.Какое линейное пространство называется конечномерным?

9.Как найти базис линейной оболочки?

1.Является ли линейным пространством множество всех радиус-векторов точек первой четверти прямоугольной декартовой системы координат?

2.Доказать, что множество A= составляет подпространство пространства A4. Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов
a1=(5,2,-3,1), a2=(4,1,-2,3), a3=(1,1,-1,-2), a4=(3,4,-1,2).

1.Является ли линейным пространством множество всех радиус-векторов точек, некоторой прямой. Найти его базис и размерность.

2.Доказать, что множество A= составляет подпространство пространства A4. Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов a1, a2, a3, a4, a5, где a1=1+2x+3×2–4×3, a2=2+3x–4×2+x3, a3=2–5x+8×2–3×3, a4=5+26x–9×2–12×3, a5=3–4x+x2+2×3.

1.Является ли линейным пространством множество всех векторов плоскости за исключением векторов, параллельных заданной прямой.

2.Доказать, что множество A= составляет подпространство пространства Pn. Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов

, , , , .

1.Составляет ли линейное пространство множество многочленов A=? Найти его размерность и базис.

2.Доказать, что множество A= составляет подпространство пространства A5. Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов a1=e1+2e2+3e3+4e4, a2=2e1+3e2+4e3+5e4, a3=3e1+4e2+5e3+6e4, a4=4e1+5e2+6e3+7e4; e1, e2, e3, e4 – базис линейного пространства L.

1.Образует ли линейное пространство множество многочленов A=? Указать его базис и размерность.

2.Доказать, что множество всех решений однородной системы линейных уравнений с n неизвестными образует подпространство пространства An. Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов
a1=2–x+3×2–2×3+4×4, a2=7×4+x3+5×2–2x+4, a3=2+x2–x+8×3+2×4.

1.Во множестве S= введены операции сложения x+y=(α1,…)+(β1,…)=(α1+β1,…) и умножения на действительное число k: kx=k(α1,α2,…)=(kα1,kα2,…). Является ли S линейным пространством, если αiÎR, i=1,2,3,…? Указать его базис и размерность.

2.Образует ли подпространство пространства V2 множество радиус-векторов точек некоторой прямой? Указать его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов

, , , .

1.Образуют ли линейное пространство множество матриц M? Указать его базис и размерность.

2.Составляет ли подпространство пространства P5 множество A=? Указать его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов a1=x5+x4+x+1, a2= –1, a3=2×2+5x, a4=2×3–2.

1.Является ли множество матриц M линейным пространством? Найти его базис и размерность.

2.Доказать, что множество 6-мерных векторов A= составляет подпространство пространства A6. Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов
a1, a2, a3, a4, где a1=e1+e2+e3+e4, a2= – e5 – e4 – e3+e2+e1, a3=2e1+2e2 – e5, a4=2e5+5e4+5e3+e2+e1, a5= – e3 – e2+e1;

e1, …, e5 – базис линейного пространства.

1.Составляет ли линейное пространство множество двумерных векторов A2= с операциями сложения x+y=(α,β)+(γ,δ)=(α+γ,β+δ) и умножения на действительное число k kx=k(α,β)=(kα,kβ)? Найти его базис и размерность.

2.Доказать, что множество матриц A составляет подпространство пространства M3. Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов
a1=3–x+3×2+2×3+5×4, a2=5–3x+2×2+3×3+4×4,

1.Доказать, что множество M2 образует линейное пространство. Найти его базис и размерность.

2.Образует ли подпространство пространства An множество A=? Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов
a1=(4,3,-5,2,3), a2=(8,6,-7,4,2),a3=(4,3,-8,2,7),a4=(4,3,1,2,-5).

1.Составляет ли линейное пространство множество векторов:

2.Составляет ли множество многочленов A= подпространство пространства Pn? Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов
a1=e1–e2+e3, a2=e1+e2+e4, a3=2e1+e3+e4; e1, e2, e3, e4 – базис линейного пространства L.

1.Составляет ли линейное пространство множество матриц A? Найти его базис и размерность.

2.Доказать, что множество A составляет подпространство пространства An. Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов a1=x+2×2+3×3–2×4+x5, a2=3×5–4×4+5×3+6×2+3x,

1.Составляет ли множество многочленов A= линейное пространство? Найти его базис и размерность.

2.Составляет ли множество матриц A подпространство пространства M2? Найти его базис и размерность.

3.Найти базис и размерность линейной оболочки векторов
a1=1–x+x2–x3+x4, a2=7×4–x3+x2+x+3, a3=1+x+3×4, a4=2×4+x3–x2+2x.

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Лабораторная работа 9

Видео:Образуют ли данные векторы базисСкачать

МАТРИЦА ПЕРЕХОДА. КООРДИНАТЫ ВЕКТОРОВ

Вопросы для самоконтроля:

1.Что называется столбцом координат (координатами) вектора в некотором базисе?

2.Дайте определение матрицы перехода от одного базиса к другому в линейном пространстве?

3.При составлении матрицы перехода координаты векторов нового базиса в старом надо располагать в строки или столбцы этой матрицы?

4.Если T – матрица перехода от первого базиса ко второму, то какой будет матрица перехода от второго базиса к первому?

5.Как связаны координаты одного и того же вектора в разных базисах?

1.Матрица M является матрицей перехода от базиса e1, e2, e3 к базису a1, a2, a3. Найти координаты векторов e1, e2, e3 и вектора x = 2e1–e3 в базисе a1, a2, a3.

2.В пространстве многочленов, степени которых не превосходят 3, найти матрицу перехода от базиса 1, x, x2, x3 к базису 3, 3x+5, (x+3)2, (x–4)3.

3.Найти связь координат одного и того же вектора в двух базисах e1=1–x, e2=2 и a1=3+2x, a2=4+3x.

1.Убедиться, что a1=(1,2,-3), a2=(4,2,-8), a3=(1,4,-1) образуют базис линейного пространства A3. Найти координаты вектора b=(7,-1,-2) в базисе a1, a2, a3.