Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Колесо радиусом 50 см вращается с частотой 60 об/мин. Какова линейная скорость вращения точек колеса, наиболее удалённых от оси вращения?
Тело движется по окружности с постоянной по модулю скоростью. Вектор импульса тела в точке А сонаправлен вектору
На рис. А показаны направления скорости и ускорения в инерциальной системе отсчёта в определённый момент времени. Какая из стрелок (1–4) на рис. Б соответствует направлению равнодействующей всех сил, действующих на тело в этот момент времени?
Космический корабль, движущийся по круговой орбите вокруг Земли, сместился на другую круговую орбиту, меньшего радиуса. Как при этом изменились сила тяготения, действующая на корабль, и модуль скорости корабля?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается 2) уменьшается 3) не изменяется
Маленькая шайба движется без трения по гладкой горке, изображённой на рисунке, не отрываясь от нее. В верхней точке A горки ускорение шайбы направлено
вниз ( ↓ )
На рисунке изображены векторы скорости и ускорения движущегося тела в некоторый момент времени. Вектор импульса тела в этот момент времени сонаправлен вектору
Космический корабль, движущийся по круговой орбите вокруг Земли, сместился на другую круговую орбиту, большего радиуса. Как при этом изменились сила тяготения, действующая на корабль со стороны Земли, и период обращения корабля вокруг Земли?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается 2) уменьшается 3) не изменяется
Направление ускорения при равномерном движении тела по окружности
всегда совпадает с направлением скорости тела
всегда совпадает с направлением перемещения тела
всегда совпадает с направлением равнодействующей силы
совпадает с направлением либо скорости тела, либо силы
На рис. А показаны направления скорости и ускорения относительно Земли в определённый момент времени. Какая из стрелок (1–4) на рис. Б соответствует направлению равнодействующей всех сил, действующих на тело в этот момент времени?
Материальная точка движется по окружности со скоростью 2 м/с. Модуль скорости точки изменился и стал равен 4 м/с. При этом
1) частота обращения точки увеличилась в 2 раза
2) частота обращения точки уменьшилась в 2 раза
3) период обращения точки увеличился в 2 раза
4) период обращения точки уменьшился в 4 раза
Скорость тела, равномерно движущегося по окружности, в любой момент времени направлена по отношению к окружности
1) по радиусу к центру
2) под углом 90º к касательной
3) по радиусу от центра
4) по касательной
На рисунке изображены векторы скорости и ускорения движущегося тела в некоторый момент времени. Вектор импульса тела в этот момент времени сонаправлен вектору
Линейная скорость движения тела по окружности увеличилась в 2 раза при неизменном радиусе окружности. Как изменилось центростремительное ускорение тела?
1) увеличилось в 2 раза
2) увеличилось в 4 раза
3) уменьшилось в 2 раза
4) уменьшилось в 4 раза
Тело движется по окружности вокруг точки О с постоянной по модулю скоростью. Какая из стрелок 1, 2, 3 или 4 указывает направление ускорения этого тела в точке А?
На рис. А показаны направления скорости и ускорения в инерциальной системе отсчёта в определённый момент времени. Какая из стрелок (1–4) на рис. Б соответствует направлению импульса тела в этот момент времени?
Радиус движения тела по окружности уменьшили в 2 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?
1) увеличилось в 2 раза
2) увеличилось в 4 раза
3) уменьшилось в 2 раза
4) уменьшилось в 4 раза
Если при движении тела по окружности модуль скорости тела не изменяется, то ускорение тела направлено
1) по радиусу окружности к её центру
2) по радиусу окружности от её центра
3) под некоторым острым углом к вектору скорости
4) по касательной к окружности
На рисунке изображены векторы скорости и силы , действующей на тело, в некоторый момент времени. Вектор импульса тела в этот момент времени сонаправлен вектору
Жук переместился на равномерно вращающемся диске из точки А в точку В. Как при этом изменились скорость вращающегося жука и частота его вращения?
Для каждой величины определите соответствующий характер изменения:
3) не изменяется
Тело равномерно движется по окружности. Куда может быть направлен вектор ускорения тела в точке 1?
4) может быть направлен произвольным образом
На рис. А показаны направления скорости и ускорения в определённый момент времени в некоей инерциальной системе отсчёта. Какая из стрелок (1–4) на рис. Б соответствует направлению равнодействующей всех сил, действующих на тело в этот момент времени?
Линейная скорость движения тела по окружности уменьшилась в 2 раза при неизменном радиусе окружности. Как изменилось центростремительное ускорение тела?
1) увеличилось в 2 раза
2) увеличилось в 4 раза
3) уменьшилось в 2 раза
4) уменьшилось в 4 раза
Тело равномерно движется по окружности. Куда может быть направлен вектор скорости тела в точке 1?
4) может быть направлен произвольным образом
На рисунке изображены векторы скорости и силы , действующей на тело, в некоторый момент времени. Вектор импульса тела в этот момент времени сонаправлен вектору
Жук переместился на равномерно вращающемся диске из точки А в точку В. Как после перемещения изменятся скорость жука и частота его вращения на диске?
Для каждой величины определите соответствующий характер изменения:
3) не изменяется
Искусственный спутник Земли равномерно движется по круговой орбите. Вектор его ускорения в любой точке
1) сонаправлен вектору скорости
2) сонаправлен вектору силы тяготения
3) сонаправлен вектору перемещения
На рис. А показаны направления скорости и ускорения тела относительно Земли в определённый момент времени. Какая из стрелок (1–4) на рис. Б соответствует направлению равнодействующей всех сил, действующих на тело в этот момент времени?
Космический корабль, движущийся по круговой орбите вокруг Земли, сместился на другую круговую орбиту, меньшего радиуса. Как после этого изменятся модуль скорости корабля и период обращения корабля вокруг Земли?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается 2) уменьшается 3) не изменяется
Маленькая шайба соскальзывает без трения по жёлобу, изображённому на рисунке. В нижней точке A жёлоба ускорение шайбы направлено
На рисунке изображены векторы скорости и ускорения движущегося тела в некоторый момент времени. Вектор силы, действующей на тело в этот момент времени, сонаправлен вектору
- Краткое описание документа:
- Дистанционное обучение как современный формат преподавания
- Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Авторская разработка онлайн-курса
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Текстовые задачи на итоговой аттестации по математике: на движение по окружности; на нахождение длины движущегося объекта; на нахождение средней скорости
- Задание №4 ОГЭ по физике
- Движение по окружности. Простые механизмы. Колебания и волны. Движение тела под действием силы тяжести.
- Теория к заданию №4 ОГЭ по физике
- Равномерное движение по окружности
- Блоки
- Условие равновесия тела (правило моментов)
- Движение тела по вертикали
- Период колебания маятника
- Волны
- Разбор типовых вариантов заданий №4 ОГЭ по физике
- Демонстрационный вариант 2018
- Первый вариант (Камзеева, № 3)
- Второй вариант (Камзеева, № 7)
- Третий вариант (Камзеева, № 11)
- 📺 Видео
Краткое описание документа:
Каждый из 10 вариантов состоит из трех заданий. Все задания взяты из банка заданий ОГЭ на сайте ФИПИ.
Структура любого варианта однотипная:
- 1-е задание — зависимость линейной и угловой скоростей от радиуса окружности; зависимость силы и ускорения в данной точке орбиты от ее линейной скорости и радиуса орбиты;
- 2-е задание — направления скорости, ускорения, равнодействующей силы, импульса для указанной точки;
- 3-е задание — нахождение направлений импульса и силы по заданным направлениям скорости и ускорения.
Один вариант помещен на листе А5, поэтому при распечатке на одном листе А4 окажутся два варианта. Всего на 10 вариантов расходуется 5 листов формата А4.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 1008 человек из 79 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Курс добавлен 23.11.2021
- Сейчас обучается 61 человек из 29 регионов
Курс повышения квалификации
Авторская разработка онлайн-курса
- Курс добавлен 02.12.2021
- Сейчас обучается 80 человек из 38 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Разбор задач на движение по окружности. ОГЭ физика 9 классСкачать

Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 530 418 материалов в базе
Другие материалы
- 04.12.2018
- 203
- 0
- 04.12.2018
- 245
- 1
- 04.12.2018
- 669
- 2
- 04.12.2018
- 285
- 0
- 04.12.2018
- 227
- 0
- 04.12.2018
- 704
- 0
- 04.12.2018
- 1250
- 27
- 04.12.2018
- 199
- 1
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 04.12.2018 4679
- DOCX 86.2 кбайт
- 18 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Холодова Мирослава Львовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 3 года и 1 месяц
- Подписчики: 0
- Всего просмотров: 4963
- Всего материалов: 2
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Физика - движение по окружностиСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Студенты на Северном Кавказе бесплатно подготовят к ЕГЭ сельских школьников
Время чтения: 1 минута
В Тюменской области школы и колледжи перевели на дистанционное обучение
Время чтения: 1 минута
В Курганской области школьников переведут на дистанционное обучение с 4 февраля
Время чтения: 1 минута
В Ингушетии школьников переведут на дистанционное обучение с 3 по 5 февраля
Время чтения: 1 минута
В Свердловской области школьников со 2 по 8 класс и студентов переводят на удаленку
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:🔴 Курс ОГЭ-2024 по физике. Урок №5. Движение по окружности. Вращательное движение | Бегунов М.И.Скачать

Текстовые задачи на итоговой аттестации по математике: на движение по окружности; на нахождение длины движущегося объекта; на нахождение средней скорости
Разделы: Математика
В статье рассмотрены задачи в помощь учащимся: для отработки навыков решения текстовых задач при подготовке к ЕГЭ, при обучении решению задач на составление математической модели реальных ситуаций во всех параллелях основной и старшей школы. В ней представлены задачи: на движение по окружности; на нахождение длины движущегося объекта; на нахождение средней скорости.
I. Задачи на движение по окружности.
Задачи на движение по окружности оказались сложными для многих школьников. Решаются они почти так же, как и обычные задачи на движение. В них также применяется формула 
Задача 1. Из пункта А круговой трассы выехал велосипедист, а через 30 мин следом за ним отправился мотоциклист. Через 10 мин после отправления он догнал велосипедиста в первый раз, а еще через 30 мин после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
Решение. Скорости участников примем за х км/ч и у км/ч. В первый раз мотоциклист обогнал велосипедиста через 10 мин, то есть через 



| Участник движения | v (км/ч.) | t(ч) | s(км) |
| велосипедист | х |  |  |
| мотоциклист | у |  |  |
Мотоциклист затем второй раз обогнал велосипедиста. Произошло это через 30 мин, то есть через 
на который надо обратить внимание. Один круг – это длина трассы, Она равна 30 км. Составим другую таблицу.
| Участник движения | v(км/ч.) | t(ч) | s(км) |
| велосипедист | х |  |  |
| мотоциклист | у |  |  |
Получим второе уравнение: 



Задачи (самостоятельно).
I.1.1. Из пункта “А” круговой трассы выехал велосипедист, а через 40 мин следом за ним отправился мотоциклист. Через 10 мин после отправления он догнал велосипедиста в первый раз, а еще через 36 мин после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 36 км. Ответ дайте в км/ч.
I.1. 2. Из пункта “А” круговой трассы выехал велосипедист, а через 30 мин следом за ним отправился мотоциклист. Через 8 мин после отправления он догнал велосипедиста в первый раз, а еще через 12 мин после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 15 км. Ответ дайте в км/ч.
I.1. 3. Из пункта “А” круговой трассы выехал велосипедист, а через 50 мин следом за ним отправился мотоциклист. Через 10 мин после отправления он догнал велосипедиста в первый раз, а еще через 18 мин после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 15 км. Ответ дайте в км/ч.
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой 20 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 15 км/ч больше скорости другого?
При одновременном старте мотоциклист, стартовавший из “А”, проехал на полкруга больше, стартовавший из “В”. То есть на 10 км. При движении двух мотоциклистов в одном направлении скорость удаления v = 



10:
Задачи (самостоятельно).
I.2.1. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой 27 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 27 км/ч больше скорости другого?
I.2.2. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой 6 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 9 км/ч больше скорости другого?
Из одной точки круговой трассы, длина которой равна 8 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 89 км/ч, и через 16 мин после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
16 мин =

х км/ч – скорость второго автомобиля.
(89 – х) км/ч – скорость удаления.
8 км – длина круговой трассы.
Уравнение.
(89 – х)
= 8,
Задачи (самостоятельно).
I.3.1. Из одной точки круговой трассы, длина которой равна 12 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 103 км/ч, и через 48 мин после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
I.3.2 . Из одной точки круговой трассы, длина которой равна 6 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 114 км/ч, и через 9 мин после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
I.3.3. Из одной точки круговой трассы, длина которой равна 20 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 105 км/ч, и через 48 мин после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
I.3.4. Из одной точки круговой трассы, длина которой равна 9 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 93 км/ч, и через 15 мин после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Часы со стрелками показывают 8 ч 00 мин. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?
Решение. Предполагаем, что экспериментально не решаем задачу.
За один час минутная стрелка проходит один круг, а часовая 

Минутная стрелка пройдет на 
1 

Значит, в первый раз стрелки поравняются через
Пусть во второй раз стрелки поравняются через время z. Минутная стрелка пройдет расстояние 1·z, а часовая 
1· z — 
Решив его, получим, что 
Итак, через 


Следовательно, если старт был в 8.00., то в четвертый раз стрелки поравняются через
4ч = 60 * 4 мин = 240 мин.
Ответ: 240 минут.
Задачи (самостоятельно).
I.4.1.Часы со стрелками показывают 4 ч 45 мин. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?
I.4.2.Часы со стрелками показывают 2 ч ровно. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?
I.4.3. Часы со стрелками показывают 8 ч 20 мин. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой? 
II. Задачи на нахождение длины движущегося объекта.
Поезд, двигаясь равномерно со скоростью 80км/ч, проезжает мимо придорожного столба за 36 с. Найдите длину состава поезда в метрах.
Решение. Так как скорость поезда указана в часах, то переведем секунды в часы.
1) 36 сек =
2) найдем длину состава поезда в километрах.
80·
Задачи (самостоятельно).
II. 2.Поезд, двигаясь равномерно со скоростью 60км/ч, проезжает мимо придорожного столба за 69 с. Найдите длину поезда в метрах. Ответ: 1150м.
II. 3. Поезд, двигаясь равномерно со скоростью 60км/ч, проезжает мимо лесополосы, длина которой 200 м, за 1мин 21 с. Найдите длину поезда в метрах. Ответ: 1150м.
III. Задачи на среднюю скорость.
На экзамене по математике может встретиться задача о нахождении средней скорости. Надо запомнить, что средняя скорость не равна среднему арифметическому скоростей. Средняя скорость находится по специальной формуле:


Если участков пути было два, то
Расстояние между двумя селами 18 км. Велосипедист ехал из одного села в другое 2ч, а возвращался по той же дороге 3ч. Какова средняя скорость движения велосипедиста на всем участке пути?
Решение:
2 ч+3 ч = 5 ч — затратил на всё движение,

Ответ: 
Турист шел со скоростью 4км/ч, потом точно такое же время со скоростью 5 км/ч. Какова средняя скорость движения туриста на всем участке пути?
Пусть турист шел t ч со скоростью 4 км/ч и t ч со скоростью 5 км/ч. Тогда за 2t ч он прошел 4t + 5t = 9t (км). Средняя скорость движения туриста равна 
Замечаем, средняя скорость движения туриста оказалась равной среднему арифметическому двух данных скоростей. Можно убедиться в том, что если время движения на двух участках пути одинаково, то средняя скорость движения равна среднему арифметическому двух данных скоростей. Для этого решим эту же задачу в общем виде.
Турист шел со скоростью 

Пусть турист шел t ч со скоростью 






Некоторое расстояние автомобиль преодолел в гору со скоростью 42 км/ч, а с горы – со скоростью 56 км/ч.
Какова средняя скорость движения автомобиля на всем участке пути?
Пусть длина участка пути равна s км. Тогда в оба конца автомобиль проехал 2 s км, затратив на весь путь 
Средняя скорость движения равна 2 s: 
Некоторое расстояние автомобиль преодолел в гору со скоростью 

Какова средняя скорость движения автомобиля на всем участке пути?
Пусть длина участка пути равна s км. Тогда в оба конца автомобиль проехал 2 s км, затратив на весь путь 
Средняя скорость движения равна 2 s: 
Ответ:
Рассмотрим задачу, в которой средняя скорость задана, а одну из скоростей нужно определить. Потребуется применение уравнения.
В гору велосипедист ехал со скоростью 10 км/ч, а с горы – с некоторой другой постоянной скоростью. Как он подсчитал, средняя скорость движения оказалась равной 12 км/ч.
С какой скоростью велосипедист ехал с горы?
Пусть в гору и с горы велосипедист проехал по s км, всего 2s км. Так как средняя скорость равна 12 км/ч, то на путь туда и обратно затрачено 



Разделим обе части уравнения на s (s 
Велосипедист ехал с горы со скоростью 15 км/ч.
Задачи (самостоятельно).
III. 1. Расстояние между двумя пунктами 45 км. Мотоциклист проехал это расстояние в одном направлении (в гору) со скоростью 40 км/ч, а в другом направлении (с горы) со скоростью 60 км/ч. Какова средняя скорость движения мотоциклиста на всем участке пути?
III. 2. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 60 км/ч, а вторую половину времени – со скоростью 46 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
III. 3.На пути из одного поселка в другой автомобиль некоторое время шел со скоростью 60 км/ч, потом точно такое же время со скоростью 40км/ч, потом точно такое же время со скоростью, равной средней скорости движения на двух первых участках пути. Какова средняя скорость движения на всем пути из одного поселка в другой?
III. 4. Велосипедист едет от дома до места работы со средней скоростью 10 км/ч, а обратно – со средней скоростью 15 км/ч, поскольку дорога идет немного под уклон. Найдите среднюю скорость движения велосипедиста на всем пути от дома до места работы и обратно.
III. 5. Автомобиль ехал из пункта А в пункт В порожняком с постоянной скоростью, а возвращался по той же дороге с грузом со скоростью 60 км/ч. С какой скоростью он ехал порожняком, если средняя скорость движения оказалась равной 70 км/ч?
III. 6. Первые 100 км автомобиль ехал со скоростью 50 км/ч, следующие 120 км – со скоростью 90 км/ч, а затем 120 км – со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
III. 7. Первые 100 км автомобиль ехал со скоростью 50 км/ч, следующие 140 км – со скоростью 80 км/ч, а затем 150 км – со скоростью 120 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
III. 8. Первые 150 км автомобиль ехал со скоростью 50 км/ч, следующие 130 км – со скоростью 60 км/ч, а затем 120 км – со скоростью 80 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
III. 9. Первые 140 км автомобиль ехал со скоростью 70 км/ч, следующие 120 км – со скоростью 80 км/ч, а затем 180 км – со скоростью 120 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Видео:Задание 21 ОГЭ. Текстовая задача. Движение по окружностиСкачать

Задание №4 ОГЭ по физике
Видео:Кинематика. Решение задач на движение по окружности. Урок 5Скачать

Движение по окружности. Простые механизмы. Колебания и волны. Движение тела под действием силы тяжести.
Для успешного решения задания №4 необходимо знание тем и разделов, приведенных в заглавии. Т.е. это материалы частично из раздела динамики (криволинейное движение, силы в природе), частично из раздела статики. Кроме того, для решения может потребоваться понимание колебательных процессов. Полезные сведения даны в разделе теории.
Теория к заданию №4 ОГЭ по физике
Равномерное движение по окружности
Движение тела по окружности можно свести к движению по очень коротким прямым линиям (хордам), которые складываются в замкнутую криволинейную траекторию. Такой подход позволяет рассматривать движение в каждый момент времени как прямолинейное и говорить о перемещении, скорости и ускорении такого движения в привычном их понимании.
В каждой точке окружности тело имеет мгновенную скорость, вектор которой совпадает с вектором перемещения в этой точке и, следовательно, направлен по касательной к окружности. При этом модуль скорости не изменяется, что и делает движение равномерным.
Ускорение в каждой точке окружности направлено к ее центру. Т.е. при движении по окружности с постоянной скоростью тело испытывает ускорение. В этом особенность такого движения, которая и обеспечивает соответствующую траекторию. Связана она с тем, что векторы скорости и ускорения имеют между собой прямой угол, и их результирующая (определяемая по правилу треугольника) удерживает тело от движения по касательной, заставляя его смещаться и держаться на одинаковом расстоянии от центра окружности.
Центростремительное ускорение может быть вычислено по формуле: 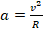
Блоки
Блок в физике – это простой механизм, обеспечивающий возможность регулирования силы, действующей на связанные с ним тела. Блок представляет собой колесо некоторой толщины с выемкой (желобом) по своей окружности. Обязательное условие для блока – возможность вращаться вокруг своей оси. По желобу проходит ремень (цепь, канат, веревка и т.д.), контакт с которым и обеспечивает вращение блока.
Блок может быть неподвижным и подвижным. Первый имеет неподвижную (зафиксированную) ось вращения, второй – подвижную.
Всякий блок – это рычаг, причем неподвижный является равноплечим рычагом, а подвижный имеет плечи, длины которых относятся между собой как 1:2. Из того, что блоки это рычаги, следует, что для них справедливо правило: проигрыш в расстоянии обеспечивает равную величину выигрыша в усилии (т.е. в силе).
Условие равновесия тела (правило моментов)
Если тело имеет неподвижную ось вращения, то оно находится в равновесии при условии, что сумма (алгебраическая) всех моментов сил, приложенных к телу, равна нулю относительно данной неподвижной оси.
Математическое выражение условия равновесия:
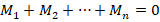
Момент силы при этом можно вычислить по формуле:
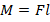
где F – приложенная сила, l – плечо силы (кратчайшее расстояния от прямой, на которой находится 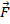
Движение тела по вертикали
Речь в данном случае идет о движении тел, брошенных вертикально вверх или опускающихся вертикально вниз. И в первом, и во втором случае имеется в виду, что на тела действует только сила тяжести, а сопротивление воздуха отсутствует.
Если тела движутся исключительно под действием силы тяжести, то это движение является равноускоренным, причем ускорение всегда одинаково. Это – ускорение своб.падения g. Величина ускорения для Земли: 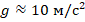
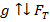
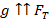
При таком движении тела скорость и высота могут быть найдены по формулам: 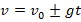
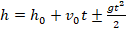
Знак «–» в формулах перед g соответствует ситуации, когда тело движется вверх, поскольку в этом случае направления векторов скорости и ускорения противоположны.
Движение тела вниз под действием силы тяжести без начальной скорости (т.е. в ситуации, когда его просто отпускают, а не бросают), называют свободным падением.
Период колебания маятника
В механике различают маятники математические и пружинные. Разница между ними заключается в том, что в первом случае тело скреплено с пружиной, а во втором – подвешено на тонкой неупругой нити. Соответственно, в пружинном маятнике тело колеблется по прямой линии, то удаляясь от положения равновесия, то возвращаясь в него, а в математическом – колеблется по дуге влево и вправо от положения равновесия.
Период колебания в пружинном маятнике вычисляется так: 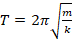
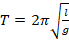
где l – длина нити, на которой подвешено тело.
Волны
В самом общем случае под волной понимают распространение колебаний от частицы к частице и от точки к точке. Различают волны механические, звуковые и др. Параметрами, описывающими характер распространения волны, являются ее длина (λ), частота ( 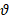
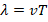
Разбор типовых вариантов заданий №4 ОГЭ по физике
Демонстрационный вариант 2018
Тело массой m, брошенное с поверхности земли вертикально вверх с начальной скоростью υ0, поднялось на максимальную высоту h0. Сопротивление воздуха пренебрежимо мало. Полная механическая энергия тела на некоторой промежуточной высоте h равна
Алгоритм решения:
- Записываем уравнение з-на сохранения энергии. Используя его, анализируем его и определяем полную энергию в граничных точках – в момент броска и при достижении телом максимальной высоты.
- Определяем полную энергию для тела в произвольный промежуточный момент времени, т.е. после того, как тело уже подброшено, но еще не достигло максимальной высоты.
- Записываем ответ.
Решение:
- Поскольку в условии есть оговорка о том, что сопротивлением воздуха можно пренебречь, то можно использовать з-н сохранения энергии. Полная энергия тела в любой момент времени, согласно закону, равна:
. Т.к. изначально тело бросают с поверхности земли с ненулевой скоростью (по условию – со скоростью v0), то в нач.момент времени
, т.е. имеет максимальную кинетич.энергию и равную нулю потенциальную. Когда тело достигает максимальной высоты, это значит, что его движение остановилось (
) и тело находится в покое на некоторой высоте над землей. В этот момент тело имеет максимальную потенц.энергию при нулевой кинетической:
.
- В процессе подъема тело одновременно находится в движении (его скорость уже не равна v0, а имеет меньшее значение v) и в то же время является телом, поднятым над землей на некую высоту h. Это значит, что полная энергия на промежуточной высоте должна быть выражена уравнением:
. Такого варианта ответа среди предложенных нет. Однако среди них есть вариант 2:
. Он содержит выражение для полной энергии в момент максимального подъема тела. Поскольку по з-ну сохранения энергии ее значение одинаково в любой момент времени, то это значит, что вариант 2 хотя и не содержит подробной расчетной формулы для вычисления полной энергии на высоте h, но отражает ее правильное количественное значение. А следовательно, именно вариант 2 является единственно правильным в данном случае.
Ответ: 2
Первый вариант (Камзеева, № 3)
Алгоритм решения:
- Переведем в СИ величины ОВ и ВА.
- Записываем ур-ние равновесия рычага.
- Записываем формулу для вычисления момента. Преобразуем ее для М1 и М2.
- Находим искомое отношение сил, используя ур-ние равновесия рычага (1).
- Записываем ответ.
Решение:
- Переведем в СИ данные в условии расстояния: ОВ=4 см=0,04 м; ВА=5 см=0,05 м.
- Согласно условию равновесия, имеем:
. Здесь М1 и М2 – соответственно моменты для F1 и F2. Примем, что положительным будет момент, направленный по часовой стрелке. Тогда получаем, что
(можно и наоборот).
- Момент силы определяется по формуле:
. Т.к.
, то
.
- Подставим выражения для моментов в (1). Получим:
. Отсюда:
.
Ответ: 2
Второй вариант (Камзеева, № 7)
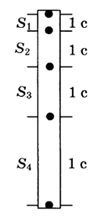
Для тела, свободно падающего из состояния покоя у поверхности некоторой планеты, измерялись расстояния, проходимые телом за последовательные равные промежутки времени (см. рис.). Чему равно ускорение свободного падения на планете, если S2=30 м? Сопротивление атмосферы пренебрежимо мало.
- 5 м/с 2
- 10 м/с 2
- 20 м/с 2
- 40 м/с 2
Алгоритм решения:
- Выражаем S1 через S2. Находим S1.
- Записываем формулу для S1 через ускорение. Выражаем из нее искомое ускорение. Вычисляем ускорение.
- Записываем ответ.
Решение:
- Известно, что при равноускоренном движении пути, проходимые телом за одинаковые временные промежутки относятся как ряд нечетных натуральных чисел, а именно:
. Исходя из этого:
.
- Поскольку тела начинает двигаться из состояния покоя (
), то
. Отсюда:
. Т.к. S1 – это путь за первую секунду, то t=1c. Тогда получаем:
.
Третий вариант (Камзеева, № 11)
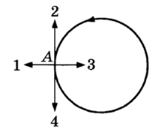
Тело движется равномерно по окружности против часовой стрелки (см. рис.). Какое направление имеет вектор ускорения в точке А?
Алгоритм решения:
- Анализируем условие. Определяем
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Решение:
Поскольку имеет место равномерное движение тела по окружности, то оно испытывает единственное ускорение – центростремительное. Его вектор всегда направлен к центру окружности. Следовательно, в т.А правильное направление – под номером 3.
📺 Видео
Физика | Равномерное движение по окружностиСкачать

🔴 ОГЭ-2022 по физике. Урок №13. Движение по окружности. Относительность движенияСкачать

ДВИЖЕНИЕ ПО ОКРУЖНОСТИ 9 класс физика ПерышкинСкачать

Урок 2. Два бегуна. Движение по окружности. ОГЭ №21. ЕГЭ №21.Скачать

Задачи на движение по окружности | Часть 11 I Физика ОГЭСкачать

Как решать задачи на движение по окружности || Задание №11 ЕГЭ 2021 || Задание №21 ОГЭ 2021Скачать

Вся физика для ОГЭ за 5 часов! | Физика ОГЭ 2023 | УмскулСкачать

⭐️ Вся кинематика для ОГЭ за 5 часов | Физика ОГЭ 2024 | УмскулСкачать

Задачи на движение | Математика TutorOnlineСкачать

ОГЭ Задание 22 Движение по кругуСкачать

Физика 9 класс. Движение по окружностиСкачать

ВСЯ МЕХАНИКА 8 ЧАСОВ I Физика ОГЭ ЕГЭ 2024 I Эмиль Исмаилов - Global_EEСкачать

ЕГЭ 2021 по физике. Движение по окружности: это надо знать всемСкачать

Кинематика. Движение по окружности. Урок 4Скачать

Насколько хорошо ты знаешь физику? #global_ee #егэфизика #огэфизикаСкачать



























 = 8,
= 8,















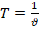
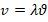
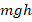
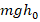
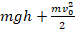
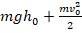
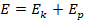 . Т.к. изначально тело бросают с поверхности земли с ненулевой скоростью (по условию – со скоростью v0), то в нач.момент времени
. Т.к. изначально тело бросают с поверхности земли с ненулевой скоростью (по условию – со скоростью v0), то в нач.момент времени 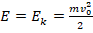 , т.е. имеет максимальную кинетич.энергию и равную нулю потенциальную. Когда тело достигает максимальной высоты, это значит, что его движение остановилось (
, т.е. имеет максимальную кинетич.энергию и равную нулю потенциальную. Когда тело достигает максимальной высоты, это значит, что его движение остановилось ( 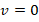 ) и тело находится в покое на некоторой высоте над землей. В этот момент тело имеет максимальную потенц.энергию при нулевой кинетической:
) и тело находится в покое на некоторой высоте над землей. В этот момент тело имеет максимальную потенц.энергию при нулевой кинетической: 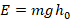 .
.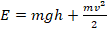 . Такого варианта ответа среди предложенных нет. Однако среди них есть вариант 2:
. Такого варианта ответа среди предложенных нет. Однако среди них есть вариант 2: 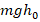 . Он содержит выражение для полной энергии в момент максимального подъема тела. Поскольку по з-ну сохранения энергии ее значение одинаково в любой момент времени, то это значит, что вариант 2 хотя и не содержит подробной расчетной формулы для вычисления полной энергии на высоте h, но отражает ее правильное количественное значение. А следовательно, именно вариант 2 является единственно правильным в данном случае.
. Он содержит выражение для полной энергии в момент максимального подъема тела. Поскольку по з-ну сохранения энергии ее значение одинаково в любой момент времени, то это значит, что вариант 2 хотя и не содержит подробной расчетной формулы для вычисления полной энергии на высоте h, но отражает ее правильное количественное значение. А следовательно, именно вариант 2 является единственно правильным в данном случае.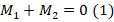 . Здесь М1 и М2 – соответственно моменты для F1 и F2. Примем, что положительным будет момент, направленный по часовой стрелке. Тогда получаем, что
. Здесь М1 и М2 – соответственно моменты для F1 и F2. Примем, что положительным будет момент, направленный по часовой стрелке. Тогда получаем, что 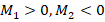 (можно и наоборот).
(можно и наоборот).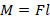 . Т.к.
. Т.к. 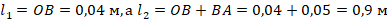 , то
, то 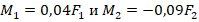 .
.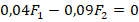 . Отсюда:
. Отсюда: 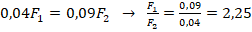 .
.
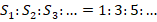 . Исходя из этого:
. Исходя из этого: 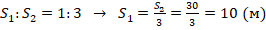 .
.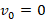 ), то
), то 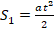 . Отсюда:
. Отсюда: 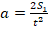 . Т.к. S1 – это путь за первую секунду, то t=1c. Тогда получаем:
. Т.к. S1 – это путь за первую секунду, то t=1c. Тогда получаем: 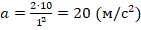 .
.