Найдите площадь четырехугольника вершинами которого являются середины ребер ad bc dd1 cc1 (6 видео)

Найдите площадь четырехугольника вершинами которого являются середины ребер ad bc dd1 cc1

Найдите площадь четырехугольника, вершины которого имеют координаты

Это задание ещё не решено, приводим решение прототипа.

Найдите площадь четырехугольника, вершины которого имеют координаты (1; 7), (8; 2), (8; 4), (1; 9).

Площадь параллелограмма равна произведению основания на высоту. Поэтому

Содержание

13. Стереометрическая задача
Решение №2665 Основание пирамиды SABC — прямоугольный треугольник АВС с прямым углом при вершине С.
Решение №2584 В правильной призме ABCDA1B1C1D1 с основанием ABCD боковое ребро равно 2, а сторона основания равна √6.
Решение №2567 В правильной призме ABCDA1B1C1D1 с основанием ABCD боковое ребро равно √3 …
Решение №2482 В правильной треугольной призме АВСА1В1С1 на рёбрах АС и ВС отмечены соответственно точки М и N так, что AM:МС = CN:BN = 2:1.
Решение №2465 Найдите площадь сечения призмы АВСА1В1С1 плоскостью MNB1, если АВ = 6, АA1 = √3.
Решение №2351 В правильной четырёхугольной пирамиде SABCD сторона основания AD равна 10, высота SH равна 12.
Решение №2312 Дана правильная треугольная пирамида SABC, сторона основания AB = 16, высота SH = 10, точка K – середина бокового ребра SА.
Решение №2045 На рёбрах CD и BB1 куба ABCDA1B1C1D1 с ребром 12 отмечены точки P и Q соответственно, причём DP = 4, а B1Q = 3. Плоскость APQ пересекает ребро CC1 в точке M.
🌟 Видео

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

13. Стереометрическая задача

Видео:Диагонали четырехугольника равны 4 и 5.Скачать

Решение №2665 Основание пирамиды SABC — прямоугольный треугольник АВС с прямым углом при вершине С.

Основание пирамиды SABC — прямоугольный треугольник АВС с прямым углом при вершине С. Высота пирамиды проходит через точку В. а) Докажите, что середина ребра SA равноудалена от вершин В и С. б) Найдите угол между плоскостью SBC и прямой, проходящей через середины рёбер ВС и SA, если известно, что BS = 2AC.

Запись опубликована: 26.12.2021
Рубрика записи13. Стереометрическая задача
Комментарии к записи:0 комментариев

Видео:№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

Решение №2584 В правильной призме ABCDA1B1C1D1 с основанием ABCD боковое ребро равно 2, а сторона основания равна √6.

В правильной призме ABCDA1B1C1D1 с основанием ABCD боковое ребро равно 2, а сторона основания равна √6. Через точку А1 перпендикулярно плоскости AB1D1 проведена прямая l. а) Докажите, что прямая l пересекает отрезок АС и делит его в отношении 2:1. б) Найдите угол между прямыми l и СD1.

Запись опубликована: 02.12.2021
Рубрика записи13. Стереометрическая задача
Комментарии к записи:0 комментариев

Видео:Найдите площадь четырёхугольникаСкачать

Решение №2567 В правильной призме ABCDA1B1C1D1 с основанием ABCD боковое ребро равно √3 …

В правильной призме ABCDA1B1C1D1 с основанием ABCD боковое ребро равно √3 , а сторона основания равна 2. Через точку А1 перпендикулярно плоскости AB1D1 проведена прямая l. а) Докажите, что прямая l пересекает отрезок АС и делит его в отношении 3:1. б) Найдите угол между прямыми l и СВ1.

Запись опубликована: 28.11.2021
Рубрика записи13. Стереометрическая задача
Комментарии к записи:0 комментариев

Видео:Найдите площадь четырёхугольникаСкачать

Решение №2482 В правильной треугольной призме АВСА1В1С1 на рёбрах АС и ВС отмечены соответственно точки М и N так, что AM:МС = CN:BN = 2:1.

В правильной треугольной призме АВСА1В1С1 на рёбрах АС и ВС отмечены соответственно точки М и N так, что AM:МС = CN:BN = 2:1. Точка К – середина ребра A1C1. а) Докажите, что плоскость MNK проходит через вершину В1. б) Найдите расстояние от точки С до плоскости KMN, если АВ = 6, АА1 = 2,4.

Запись опубликована: 10.11.2021
Рубрика записи13. Стереометрическая задача
Комментарии к записи:0 комментариев

Видео:Найдите площадь четырёхугольникаСкачать

Решение №2465 Найдите площадь сечения призмы АВСА1В1С1 плоскостью MNB1, если АВ = 6, АA1 = √3.

В правильной треугольной призме АВСА1В1С1 на рёбрах АС и ВС отмечены соответственно точки М и N так, что AM:МС = CN:BN = 2:1. а) Докажите, что плоскость MNB1 проходит через середину ребра A1C1. б) Найдите площадь сечения призмы АВСА1В1С1 плоскостью MNB1, если АВ = 6, АA1 = √3.

Запись опубликована: 08.11.2021
Рубрика записи13. Стереометрическая задача
Комментарии к записи:0 комментариев

Видео:Задача 6 №27436 ЕГЭ по математике. Урок 50Скачать

Решение №2351 В правильной четырёхугольной пирамиде SABCD сторона основания AD равна 10, высота SH равна 12.

В правильной четырёхугольной пирамиде SABCD сторона основания AD равна 10, высота SH равна 12. Точка К – середина бокового ребра SD. Плоскость АКВ пересекает боковое ребро SC в точке Р. а) Докажите, что площадь четырёхугольника CDKP составляет 3/4 площади треугольника SCD. б) Найдите объем пирамиды ACDKP.

Запись опубликована: 25.10.2021
Рубрика записи13. Стереометрическая задача
Комментарии к записи:0 комментариев

Видео:Стереометрия, номер 10.1Скачать

Решение №2312 Дана правильная треугольная пирамида SABC, сторона основания AB = 16, высота SH = 10, точка K – середина бокового ребра SА.

Дана правильная треугольная пирамида SABC, сторона основания AB = 16, высота SH = 10, точка K – середина бокового ребра SА. Плоскость, параллельная плоскости АВС, проходит через точку K и пересекает ребра SB и SC в точках Q и P соответственно. а) Докажите, что площадь четырёхугольника BCPQ составляет 3/4 площади треугольника SBC б) Найдите объем пирамиды KBCPQ.

Запись опубликована: 15.10.2021
Рубрика записи13. Стереометрическая задача
Комментарии к записи:0 комментариев

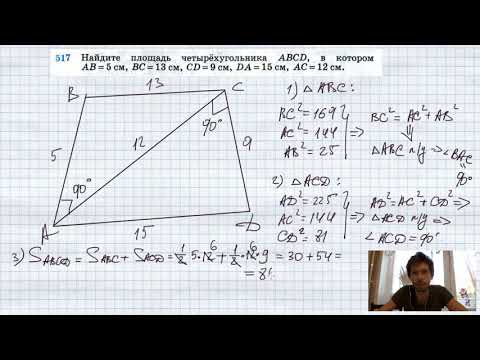
Видео:№517. Найдите площадь четырехугольника ABCD, в котором АВ = 5 см, ВС = 13 см, CD = 9 см, DA =15 смСкачать

Решение №2045 На рёбрах CD и BB1 куба ABCDA1B1C1D1 с ребром 12 отмечены точки P и Q соответственно, причём DP = 4, а B1Q = 3. Плоскость APQ пересекает ребро CC1 в точке M.

На рёбрах CD и BB1 куба ABCDA1B1C1D1 с ребром 12 отмечены точки P и Q соответственно, причём DP = 4, а B1Q = 3. Плоскость APQ пересекает ребро CC1 в точке M. а) Докажите, что точка M является серединой ребра CC1 . б) Найдите расстояние от точки C до плоскости APQ.