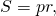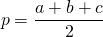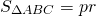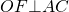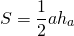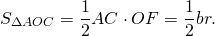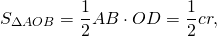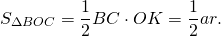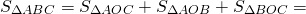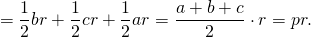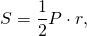Площадь треугольника одна вторая периметра на радиус вписанной окружности

Видео:Задание 24 Площадь описанного треугольникаСкачать

Определение площади треугольника

Площадь треугольника — это величина, которая
показывает какие размеры у треугольника.

Сейчас, на примере покажем, что такое площадь,
а также, как можно найти площадь треугольника.

Площадь треугольника, можно очень легко объяснить
на примере прямоугольного треугольника в клеточном поле.
Площадь, в нашем случае, будет равна количеству клеток.

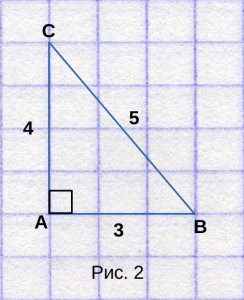
Для наглядности, нарисуем прямоугольный треугольник
ABC, со длинами сторон 3, 4 и 5, как на рисунке 2. Отметим, что он прямоугольный.

Посчитаем количество клеток, которые занимает треугольник.
3 полных клетки, и 4 неполных клетки, но для того, чтобы узнать
площадь треугольника в клеточном поле нам нужно узнать количество
полных клеток, которые занимает весь треугольник. Наша задача в том,
чтобы неполные клетки преобразовать в полные.

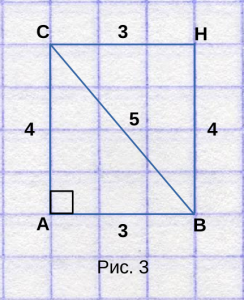
Для этого нарисуем второй треугольник, так,
чтобы получился прямоугольник, как на рисунке 3.

Как видим, весь прямоугольник занимает 12 полных клеток.

Формула площади прямоугольника равна произведению
одной стороны на другую — ​ ( S = ab ) ​,
поэтому площадь прямоугольника равна 3 * 4 = 12 клеткам.

Площадь треугольника, из которого состоит прямоугольник,
можно найти по другой формуле: ​ ( S = frac2 ab ) ​.
Подставив значения длин сторон, получаем — S = 0.5 * 3 * 4,
из чего следует, что S = 6 клетками, или же квадратным сантиметрам.

Прямоугольник можно условно разделить
на два треугольника, поэтому площадь треугольника
равна половине площади прямоугольника.

Формула площади треугольника — это формула,
по которой можно найти площадь треугольника.

Формулы площади треугольника применяют, только,
и только тогда, когда невозможно узнать площадь
треугольника, глядя на рисунок, или просто посчитав клетки.

Видео:Задача 6 №27624 ЕГЭ по математике. Урок 71Скачать

Формулы площади треугольника

Ⅰ. Через высоту и основание

a — сторона, на которую падает высота,
b — высота.

Самая известная формула площади треугольника.
Зная только высоту и сторону, на которую падает
эта высота, можно найти площадь треугольника.

Ⅱ. Через все стороны и периметр

p — полупериметр, вычисляется по формуле: ​ ( p = frac ) ​,
a, b, c — стороны треугольника.

Это формулу, нужно использовать когда известны
все три стороны треугольника. Зная три стороны
треугольника можно найти периметр, а дальше
найти и площадь заданного треугольника.

Эту формулу площади также называют формулой Герона.

Ⅲ. Через две стороны и угол между ними

[ S = frac a cdot b cdot sin β ]

a, b — стороны между которыми расположен угол β,
sin β — синус угла β.

Формула применяется, когда известен
один из углов, и две стороны, образующие
этот угол. В некоторых задачах площадь
треугольника можно найти только по этой формуле.

Ⅳ. Через периметр и радиус вписанной окружности

[ S = r cdot frac

2 ]

r — радиус вписанной окружности,
P — периметр треугольника.

Тут даже не обязательно знать все стороны треугольника,
достаточно знать периметр и радиус описанной окружности.

Ⅴ. Через все стороны и радиус описанной окружности

abc — произведение всех сторон треугольника,
R — радиус описанной окружности.

Пожалуй, единственная формула, где площадь
треугольника можно найти только через радиус
описанной окружности и произведение трех сторон.

Ⅵ. Через сторону и два прилежащих к ней угла

a — сторона треугольника,
sin α — синус угла α,
sin β — синус угла β.

Готов поспорить, вы даже ни разу не видели этой формулы.
Эта очередная формула площади треугольника, применяется
в крайне редких случаях — когда известны два угла и сторона,
к которой эти углы примыкают.

Видео:Площадь треугольника через радиус вписанной окружностиСкачать

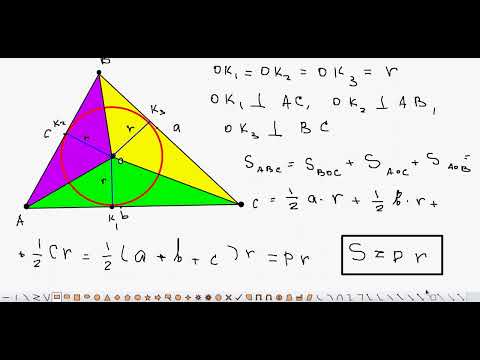
Площадь треугольника через радиус вписанной окружности

Как найти площадь треугольника через радиус вписанной окружности?

Площадь треугольника равна произведению радиуса вписанной в этот треугольник окружности на на его полупериметр.

Формула для нахождения площади треугольника через радиус вписанной окружности:

окружность (O; r) — вписанная,

Рассмотрим треугольник AOC.

(как радиус, проведенный в точку касания).

Следовательно, OF — высота треугольника AOC.

Так как площадь треугольника ABC равна сумме площадей этих треугольников, то

Что и требовалось доказать.

Если требуется найти площадь треугольника через его периметр, формулу записывают так:

где P — периметр треугольника, r — радиус вписанной в этот треугольник окружности.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

2 Comments

Полезно, вспомнить курс школьной геометрии.
Разработчики сайта дерзайте дальше.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.

Видео:Геометрия Периметр треугольника равен 32 см а радиус вписанной окружности 1,5 см Найдите площадьСкачать

Если треугольник прямоугольный

То есть один из его углов равен 90 градусам.

Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Видео:Площадь квадрата. Как найти площадь квадрата?Скачать

Если он равнобедренный

То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Если он равносторонний

То есть все три стороны равны. Ваши действия такие:

1. Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
2. Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
3. Поделите все на 4.

Видео:Уравнение годаСкачать

Если известна сторона и высота

Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.

Видео:Формулы площади треугольника. Вписаная и описаная окружностьСкачать

Если известны две стороны и градус угла между ними

Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Видео:Площадь треугольника и вписанная окружностьСкачать

Если известны длины трех сторон

1. Найдите периметр. Для этого сложите все три стороны.
2. Найдите полупериметр – разделите периметр на два. Запомните значение.
3. Отнимите от полупериметра длину первой стороны. Запомните.
4. Отнимите от полупериметра длину второй стороны. Тоже запомните.
5. Отнимите от полупериметра длину третьей стороны. И ее запомните.
6. Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
7. Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.

Видео:Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Если известны три стороны и радиус описанной окружности

Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Видео:Формулы площади треугольникаСкачать

Если известны три стороны и радиус вписанной окружности

Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.

Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.

🎦 Видео

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Геометрия Доказательство Площадь треугольника равна произведению его полупериметра и радиусаСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Формулы равностороннего треугольника #shortsСкачать

Геометрия Площадь треугольника равна 84 см2 а его периметр 72 см Найдите радиус окружности вписаннойСкачать

Секретные формулы площади треугольникаСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать