Вписанная в треугольник авс окружность с центром о касается

Задание. Окружность с центром О, вписанная в треугольник АВС, касается его сторон АВ, АС и ВС в точках С₁, В₁ и А₁ соответственно. Биссектриса угла А пересекает эту окружность в точке Q, лежащей внутри треугольника АВ₁С₁.

а) Докажите, что С₁Q – биссектриса угла АС₁В₁.

б) Найдите расстояние от точки О до центра окружности, вписанной в треугольник АС₁В₁, если известно, что ВС = 15, АВ = 13, АС = 14.

Решение:

Угол ∠QB₁C₁ – вписанный в окружность угол, он равен половине дуги, на которую он опирается, т. е.

Так как АВ – касательная к окружности и QC₁ – хорда окружности, то угол между хордой и касательной окружности, проведенной через конец хорды, равен половине дуги, лежащей внутри этого угла, т. е.

б) Найдите расстояние от точки О до центра окружности, вписанной в треугольник АС₁В₁, если известно, что ВС = 15, АВ = 13, АС = 14.

Так как AQ и C₁Q – биссектрисы треугольника ∆AB₁C₁, тогда точка пересечения биссектрис Q – центр вписанной в треугольник ∆AB₁C₁ окружности. Точка Q – точка пересечения биссектрисы AQ и окружности с центром О, то расстоянием от точки О до точки Q – центра окружности, вписанной в треугольник ∆AB₁C₁ является OQ – радиус окружности с центром О, вписанный в треугольник ∆АВС.

P = 13 + 15 + 14 = 42

Площадь треугольника ∆АВС найдем по формуле Герона:

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

В треугольник АВС вписана окружность с центром О, которая касается его сторон АВ, ВС и АС соответственно в точках М, N и K. Найдите:

Видео:№16 Профильный ЕГЭ. Окружность с центром О, вписанная в прямоугольный треугольник ABC касаетсяСкачать

Ваш ответ

Видео:Урок 3. №23 ОГЭ. Касательная. Окружность с центром на стороне AC касается АВ в точке В.Скачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,044
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Геометрия 8 Бутузов КР-1

Геометрия 8 Бутузов КР-1. Контрольная работа по геометрии 8 класс с ответами по учебнику Бутузова «Геометрия 8 класс» п/р Садовничего. Цитаты из пособия «Геометрия. Дидактические материалы. 8 класс / Бутузов и др. — М. : Просвещение» использованы в учебных целях.

Видео:Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

Контрольная работа 1 по геометрии
(8 класс, УМК Бутузов и др.)

КР-1. ВАРИАНТ 1

1. Могут ли две стороны треугольника быть параллельными одной прямой?
2. На сторонах АВ и ВС треугольника АВС отмечены точки М и N так, что MN || АС. Найдите угол CNM, если ∠C = 70°.
3. Окружность, вписанная в треугольник АВС, касается стороны ВС в точке D. Докажите, что если отрезок AD — медиана треугольника, то АВ = АС.
4. Точка О — центр окружности, описанной около остроугольного треугольника АВС. Найдите углы треугольника, если ∠BAO = 20° и ∠CAO = 30°.

КР-1. ВАРИАНТ 2

1. Прямая параллельна стороне АВ угла АВС. Пересекает ли она прямую ВС?
2. Угол АВС равен 64°. Прямая, проходящая через точку А параллельно прямой ВС, пересекает биссектрису угла АВС в точке D. Найдите углы треугольника ABD.
3. Окружность, вписанная в треугольник АВС, касается стороны ВС в точке D. Докажите, что если луч AD — биссектриса угла треугольника, то АВ = АС.
4. Точка О — центр окружности, описанной около остроугольного треугольника АВС. Найдите углы ВАО и САО, если ∠A = 60° и ∠B = 40°.

КР-1. ВАРИАНТ 3

1. Внешние углы треугольника АВС с вершинами А и В равны 130° и 140°. На сторонах АС и ВС отмечены точки М и N так, что MN || АВ. Найдите углы треугольника CMN.
2. Окружность касается сторон АВ, ВС и СА треугольника АВС в точках К, L и М соответственно, причём МК = ML. Докажите, что луч КМ — биссектриса угла AKL.
3. Прямая пересекает боковую сторону АС, основание ВС и продолжение боковой стороны АВ (за точку В) равнобедренного треугольника АВС в точках К, L и М соответственно. Найдите угол А, если известно, что треугольники BML и CKL равнобедренные.
4. Вписанная в треугольник АВС окружность касается его сторон в точках L, М и N. Докажите, что треугольник LMN остроугольный.

КР-1. ВАРИАНТ 4

1. На медиане ВМ равнобедренного треугольника АВС с основанием АС отмечена точка Е и через неё проведены прямые, параллельные сторонам АВ и ВС. Эти прямые пересекают отрезки AM и СМ в точках F и G соответственно. Докажите, что AF = CG.
2. Окружность касается сторон АВ, ВС и СА треугольника АВС в точках К, L и М соответственно, причём луч КМ — биссектриса угла AKL. Докажите, что АВ = ВС.
3. Прямая пересекает боковую сторону АС, основание ВС и продолжение боковой стороны АВ (за точку В) равнобедренного треугольника АВС в точках К, L и М соответственно. Найдите угол МВС, если известно, что треугольники BML и CKL равнобедренные.
4. Вписанная в треугольник АВС окружность касается сторон АВ, ВС и АС в точках L, М и N. Найдите угол LMN, если ∠А = 80°.

Ответы на контрольную работу:

ОТВЕТЫ с указанием как решать задания

Геометрия 8 Бутузов КР-1. Контрольная работа по геометрии 8 класс с ответами по учебнику Бутузова «Геометрия 8 класс» п/р Садовничего (МГУ школе).

Добавить комментарий Отменить ответ

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

💥 Видео

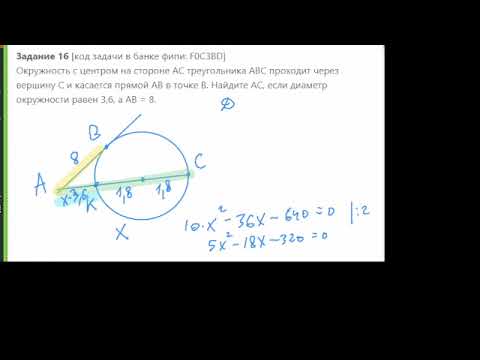
Окружность с центром на стороне AС треугольника ABC проходит через вершину С и касается прямой AB вСкачать

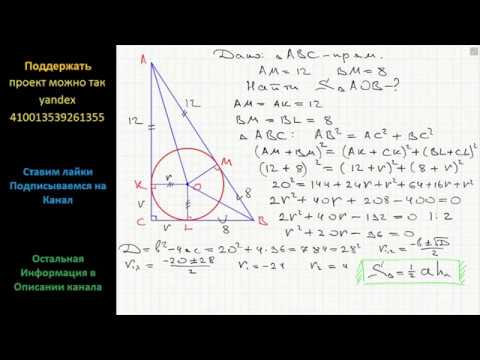
Геометрия Окружность с центром О вписана в прямоугольный треугольник АВС. Она касается гипотенузы АВСкачать

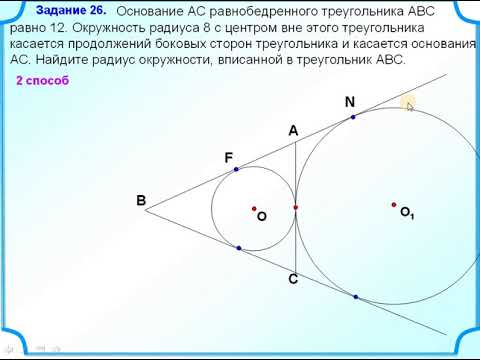
Окружность, вписанная в треугольник. Как найти центр и радиус. Геометрия 7-8 классСкачать

ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Вневписанная окружностьСкачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

[ОГЭ] Найдите боковую сторону АВ трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120Скачать

2034 треугольник ABC вписан в окружность с центром в точке O точки O и C лежат в одной полуплоскостиСкачать

ОГЭ Задание 25 Демонстрационный вариант 2022, математикаСкачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

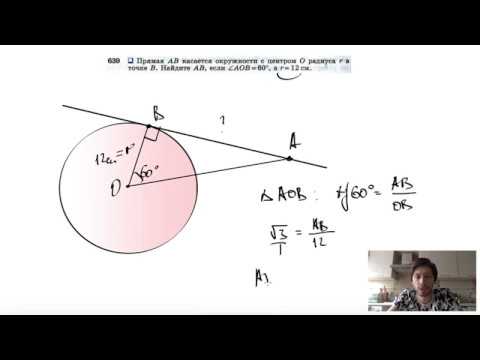
№639. Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВСкачать

Треугольник ABC вписан в окружность с центром O Угол BAC равен 32°Скачать

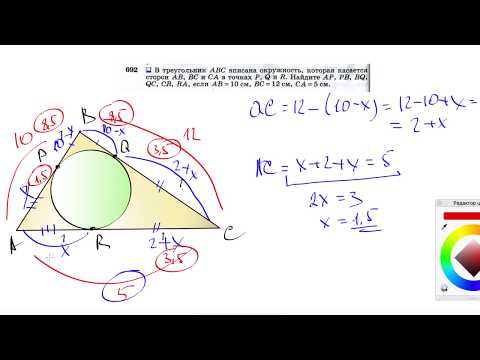
№692. В треугольник ABC вписана окружность, которая касается сторон АВ, ВС и СА в точках Р, Q и RСкачать

Окружность вписанная в прямоугольный треугольник АВС касается катетов АС и ВС в точках М и N соответСкачать

№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать