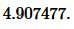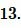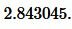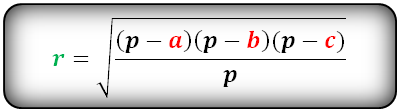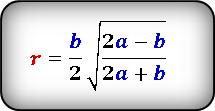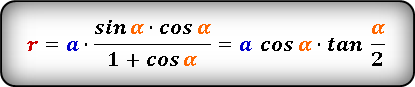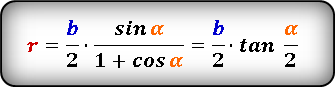С помощю этого онлайн калькулятора можно найти радиус вписанной в любой треугольник окружности, в том числе радиус вписанной в равносторонний треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
- 1. Радиус вписанной в равносторонний треугольник окружности, если известна сторона треугольника
- 2. Радиус вписанной в равносторонний треугольник окружности, если известна высота треугольника
- 3. Радиус вписанной в равносторонний треугольник окружности, если известна площадь треугольника
- Треугольник вписанный в окружность
- Определение
- Формулы
- Радиус вписанной окружности в треугольник
- Радиус описанной окружности около треугольника
- Площадь треугольника
- Периметр треугольника
- Сторона треугольника
- Средняя линия треугольника
- Высота треугольника
- Свойства
- Доказательство
- Все формулы для радиуса вписанной окружности
- Радиус вписанной окружности в треугольник
- Радиус вписанной окружности в равносторонний треугольник
- Радиус вписанной окружности равнобедренный треугольник
- 🎬 Видео
Видео:ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

1. Радиус вписанной в равносторонний треугольник окружности, если известна сторона треугольника
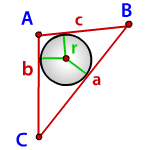
Пусть известна сторона a равностороннего треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной в треугольник окружности.
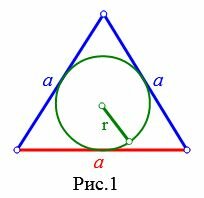 |
Радиус вписанной в равнобедренный треугольник окружности через основание a и боковую сторону b вычисляется из следующей формулы:
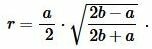 | (1) |
Учитывая, что у равностороннего треугольника все стороны равны (( small a=b )), имеем:
| ( small r=frac cdot sqrt<frac> ) ( small =frac cdot sqrt<frac> ) ( small =frac<large 2 cdot sqrt> ) |
| ( small r=frac<large 2 cdot sqrt> ) | (2) |
или, умножив числитель и знаменатель на ( small sqrt ):
| ( small r=frac<large sqrt> cdot a ) | (3) |
Пример 1. Известна сторона a=17 равностороннего треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся одним из формул (2) и (3). Подставим значения ( small a=17 ) в (3):
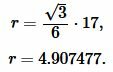 |
Ответ:
Видео:Окружность вписана в равносторонний треугольник, найти радиусСкачать

2. Радиус вписанной в равносторонний треугольник окружности, если известна высота треугольника
Пусть известна высота h равностороннего треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
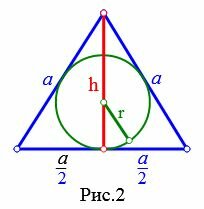 |
Выведем формулу стороны равностороннего треугольника через высоту. Из Теоремы Пифагора имеем:
| ( small h^2+left( frac right) ^2=a^2.) |
| ( small h^2+ frac =a^2; ; ) ( small fraca^2 =h^2; ; ) ( small a^2=frac.) |
| ( small a= frac<large sqrt> .) | (4) |
Формула радиуса вписанной в равнобедренный треугольник окружности по основанию и высоте вычисляется из формулы
| ( small r= large frac<a+sqrt> ) | (5) |
Подставляя (4) в (5), получим:
| ( small r= large frac<frac<large sqrt>><frac<large sqrt>+sqrt<frac+4h^2>> ) ( small = large frac<frac<large sqrt>><frac<large sqrt>+sqrt<frac>> ) ( small = large frac<frac<large sqrt>><frac<large sqrt>+frac<large sqrt>> ) ( small = large fracsmall =large frac small cdot h ) |
То есть, радиус вписанной в равносторонний треугольник окружности по высоте вычисляется из формулы:
| ( small r = large frac small cdot h ) | (6) |
Пример 2. Известна высота ( small h=39 ) равностороннего треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значение ( small h=39 ) в (6):
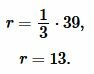 |
Ответ:
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

3. Радиус вписанной в равносторонний треугольник окружности, если известна площадь треугольника
Пусть известна площадь S равностороннего треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
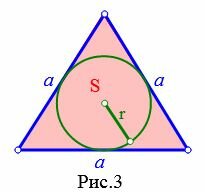 |
Площадь равностороннего треугольника по радиусу вписанной окружности вычисляется из следующей формулы:
| ( small S= 3cdot sqrtr^2.) |
| ( small r^2= large frac |
| ( small r= large frac <sqrt[4]> small cdot sqrt | (7) |
Пример 3. Известна площадь равностороннего треугольника: ( small S=42 . ) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (7). Подставим значение ( small S=42 ) в (7):
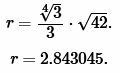 |
Ответ:
Видео:Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать

Треугольник вписанный в окружность
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:
Площадь треугольника
S — площадь треугольника.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:
Площадь треугольника вписанного в окружность,
если известен полупериметр:
Площадь треугольника вписанного в окружность,
если известен высота и основание:
Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:
Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:
[ S = fracab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:
Сторона треугольника
a — сторона треугольника.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:
Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:
Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:
[ h = b cdot sin alpha ]
Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:
Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Видео:Равносторонний треугольник в окружностиСкачать

Доказательство
Около любого треугольника, можно
описать окружность притом только одну.
окружность и треугольник,
которые изображены на рисунке 2.
окружность описана
около треугольника.
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
Видео:Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

Все формулы для радиуса вписанной окружности
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Радиус вписанной окружности в треугольник
a , b , c — стороны треугольника
p — полупериметр, p=( a + b + c )/2
Формула радиуса вписанной окружности в треугольник ( r ):
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Радиус вписанной окружности в равносторонний треугольник
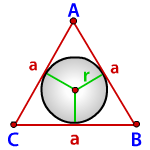
a — сторона треугольника
r — радиус вписанной окружности
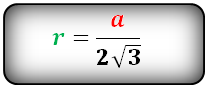
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):
Видео:Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать

Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
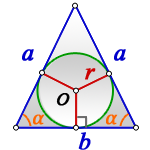
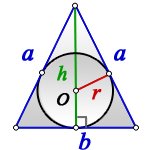
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
α — угол при основании
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :
🎬 Видео
Равносторонний треугольник вписан в окружность. Найти площадь меньшего сегмента.Скачать

Равносторонний треугольник. Описанная окружностьСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

№693. В прямоугольный треугольник вписана окружность радиуса r. Найдите периметр треугольника,Скачать
Всё про углы в окружности. Геометрия | МатематикаСкачать

Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать

15 задание треугольники огэ по математике / маттаймСкачать