Найдите объем призмы если в ее основании лежит четырехугольник площадь 5 а боковые (8 видео)

Найдите объем призмы если в ее основании лежит четырехугольник площадь 5 а боковые

Задание 8. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны 2√3 и наклонены к плоскости основания под углом 30°.

Объем призмы вычислим как произведение площади основания на ее высоту

В основании призмы лежит правильный шестиугольник со сторонами 2. Его площадь равна площади 6 равносторонним треугольникам со сторонами 2 (см. рисунок ниже).

Площадь одного такого треугольника можно найти как

и площадь основания равна

Так как ребра призмы наклонены под 30° к основанию, то высота призмы будет равна

Таким образом, объем призмы равен

Содержание

Как найти объём прямой призмы, основанием которой служит данный четырёхугольник, а боковое ребро равно 5 см?
Ваш ответ
решение вопроса
Похожие вопросы
Объём и площадь поверхности правильной четырёхугольной призмы
Как выглядит призма
Площадь поверхности и объём
Нахождение элементов призмы
Примеры задач с решениями
🎥 Видео

Видео:Площадь поверхности призмы. 11 класс.Скачать

Как найти объём прямой призмы, основанием которой служит данный четырёхугольник, а боковое ребро равно 5 см?

Видео:КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

Ваш ответ

Видео:🔴 В основании прямой призмы лежит прямоугольный ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

решение вопроса

Видео:ЕГЭ математика задача 2 вариант 8Скачать

Объём и площадь поверхности правильной четырёхугольной призмы

В школьной программе по курсу стереометрии изучение объёмных фигур обычно начинается с простого геометрического тела — многогранника призмы. Роль её оснований выполняют 2 равных многоугольника, лежащих в параллельных плоскостях. Частным случаем является правильная четырёхугольная призма. Её основами являются 2 одинаковых правильных четырёхугольника, к которым перпендикулярны боковые стороны, имеющие форму параллелограммов (или прямоугольников, если призма не наклонная).

Видео:11 класс, 31 урок, Объем прямой призмыСкачать

Как выглядит призма

Правильной четырёхугольной призмой называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками. Иное название для этой геометрической фигуры — прямой параллелепипед.

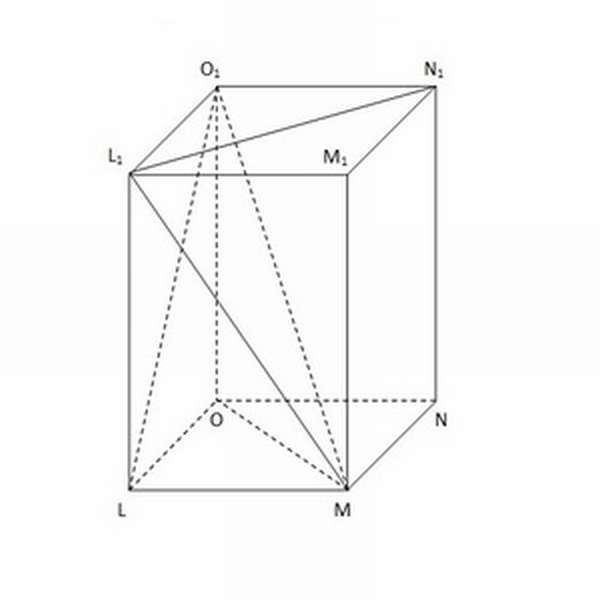
Рисунок, на котором изображена четырёхугольная призма, показан ниже.

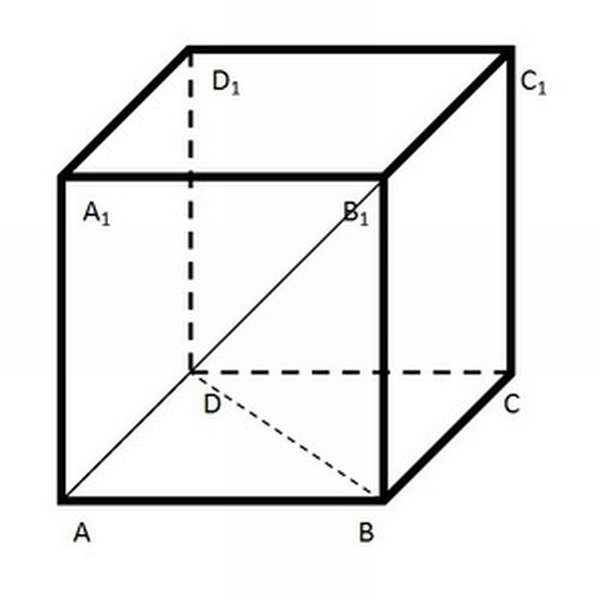
На картинке также можно увидеть важнейшие элементы, из которых состоит геометрическое тело. К ним принято относить:

Основы призмы — квадраты LMNO и L₁M₁N₁O₁.
Боковые грани — прямоугольники MM₁L₁L, LL₁O₁O, NN₁O₁O и MM₁N₁N, расположенные под прямым углом к основаниям.
Боковые рёбра — отрезки, расположенные на стыке между двумя боковыми гранями: M₁M, N₁N, O₁O и L₁L. Также выполняют роль высоты (поскольку лежат в параллельной основаниям плоскости). В призме боковые рёбра всегда равны между собой — это одно из важнейших свойств этого геометрического тела.
Диагонали, которые, в свою очередь, подразделяются ещё на 3 категории. К ним относится 4 диагонали основания (MO, N₁L₁), 8 диагоналей боковых граней (ML₁, O₁L) и 4 диагонали призмы, начала и концы которых являются вершинами 2 разных оснований и боковых сторон (MO₁, N₁L).

Иногда в задачах по геометрии можно встретить понятие сечения. Определение будет звучать так: сечение — это все точки объёмного тела, принадлежащие секущей плоскости. Сечение бывает перпендикулярным (пересекает рёбра фигуры под углом 90 градусов). Для прямоугольной призмы также рассматривается диагональное сечение (максимальное количество сечений, которых можно построить — 2), проходящее через 2 ребра и диагонали основания.

Если же сечение нарисовано так, что секущая плоскость не параллельна ни основам, ни боковым граням, в результате получается усечённая призма.

Для нахождения приведённых призматических элементов используются различные отношения и формулы. Часть из них известна из курса планиметрии (например, для нахождения площади основания призмы достаточно вспомнить формулу площади квадрата).

Видео:ЕГЭ-2021: Объём отсечённой призмы | Задание 8: СтереометрияСкачать

Площадь поверхности и объём

Чтобы определить объём призмы по формуле, необходимо знать площадь её основания и высоту:

Так как основанием правильной четырёхгранной призмы является квадрат со стороной a, можно записать формулу в более подробном виде:

Если речь идёт о кубе — правильной призме с равной длиной, шириной и высотой, объём вычисляется так:

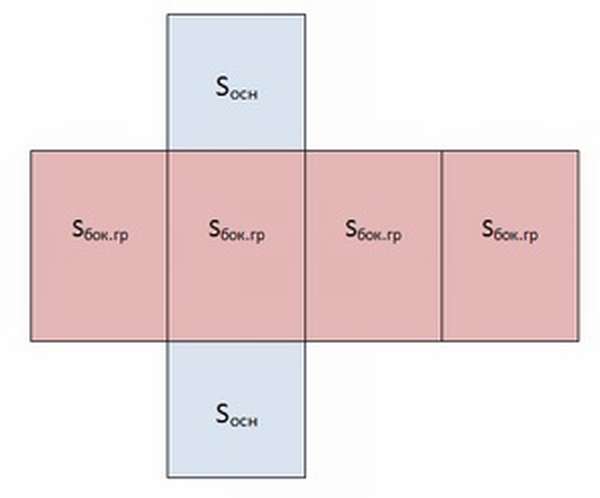
Чтобы понять, как найти площадь боковой поверхности призмы, необходимо представить себе её развёртку.

Из чертежа видно, что боковая поверхность составлена из 4 равных прямоугольников. Её площадь вычисляется как произведение периметра основания на высоту фигуры:

С учётом того, что периметр квадрата равен P = 4a, формула принимает вид:

Для вычисления площади полной поверхности призмы нужно к боковой площади прибавить 2 площади оснований:

Sполн = Sбок + 2Sосн

Применительно к четырёхугольной правильной призме формула имеет вид:

Для площади поверхности куба:

Зная объём или площадь поверхности, можно вычислить отдельные элементы геометрического тела.

Видео:🔴 Найдите объём правильной четырёхугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Нахождение элементов призмы

Часто встречаются задачи, в которых дан объём или известна величина боковой площади поверхности, где необходимо определить длину стороны основания или высоту. В таких случаях формулы можно вывести:

длина стороны основания: a = Sбок / 4h = √(V / h),
длина высоты или бокового ребра: h = Sбок / 4a = V / a²,
площадь основания: Sосн = V / h,
площадь боковой грани: Sбок. гр = Sбок / 4.

Чтобы определить, какую площадь имеет диагональное сечение, необходимо знать длину диагонали и высоту фигуры. Для квадрата d = a√2. Из этого следует:

Для вычисления диагонали призмы используется формула:

Чтобы понять, как применять приведённые соотношения, можно попрактиковаться и решить несколько несложных заданий.

Видео:Призма и пирамида. Площадь и объем. Вебинар | Математика 10 классСкачать

Примеры задач с решениями

Вот несколько заданий, встречающихся в государственных итоговых экзаменах по математике.

В коробку, имеющую форму правильной четырёхугольной призмы, насыпан песок. Высота его уровня составляет 10 см. Каким станет уровень песка, если переместить его в ёмкость такой же формы, но с длиной основания в 2 раза больше?

Следует рассуждать следующим образом. Количество песка в первой и второй ёмкости не изменялось, т. е. его объём в них совпадает. Можно обозначить длину основания за a. В таком случае для первой коробки объём вещества составит:

Для второй коробки длина основания составляет 2a, но неизвестна высота уровня песка:

Поскольку V₁ = V₂, можно приравнять выражения:

После сокращения обеих частей уравнения на a² получается:

В результате новый уровень песка составит h = 10 / 4 = 2,5 см.

ABCDA₁B₁C₁D₁ правильная призма. Известно, что BD = AB₁ = 6√2. Найти площадь полной поверхности тела.

Чтобы было проще понять, какие именно элементы известны, можно изобразить фигуру.

Поскольку речь идёт о правильной призме, можно сделать вывод, что в основании находится квадрат с диагональю 6√2. Диагональ боковой грани имеет такую же величину, следовательно, боковая грань тоже имеет форму квадрата, равного основанию. Получается, что все три измерения — длина, ширина и высота — равны. Можно сделать вывод, что ABCDA₁B₁C₁D₁ является кубом.

Длина любого ребра определяется через известную диагональ:

a = d / √2 = 6√2 / √2 = 6

Площадь полной поверхности находится по формуле для куба:

Sполн = 6a² = 6·6² = 216

В комнате производится ремонт. Известно, что её пол имеет форму квадрата с площадью 9 м². Высота помещения составляет 2,5 м. Какова наименьшая стоимость оклейки комнаты обоями, если 1 м² стоит 50 рублей?

Поскольку пол и потолок являются квадратами, т. е. правильными четырёхугольниками, и стены её перпендикулярны горизонтальным поверхностям, можно сделать вывод, что она является правильной призмой. Необходимо определить площадь её боковой поверхности.

Длина комнаты составляет a = √9 = 3 м.

Обоями будет оклеена площадь Sбок = 4·3·2,5 = 30 м².

Наименьшая стоимость обоев для этой комнаты составит 50·30 = 1500 рублей.

Таким образом, для решения задач на прямоугольную призму достаточно уметь вычислять площадь и периметр квадрата и прямоугольника, а также владеть формулами для нахождения объёма и площади поверхности.