Как определить периметр треугольника в окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Определение

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.

Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

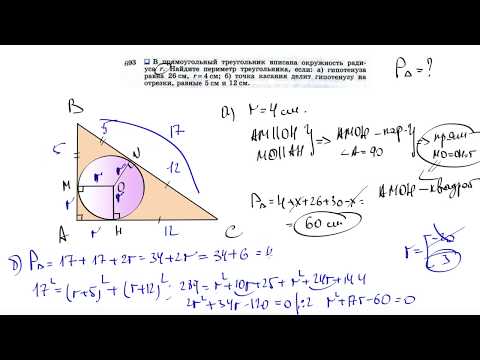
Видео:№693. В прямоугольный треугольник вписана окружность радиуса r. Найдите периметр треугольника,Скачать

Как узнать периметр треугольника

Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.

Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.

P = a + b + c, где a, b, c — длина стороны.

Если известна площадь и радиус вписанной окружности:

P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.

Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:

P = √ b 2 + с 2 — 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.

Если известна одна сторона в равностороннем треугольнике:

P = 3 * a, где a — длина стороны.

Все стороны в равносторонней фигуре равны.

Если известна боковая сторона и основание в равнобедренном треугольнике:

P = 2 * a + b, где a — боковая сторона, b — основание.

Боковые стороны в равнобедренной фигуре равны.

Если известна боковая сторона и высота в равнобедренном треугольнике:

P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.

Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.

Если известны катеты в прямоугольном треугольнике:

P = √ a 2 + b 2 + (a + b), где a, b — катеты.

Катет — одна из двух сторон, которые образуют прямой угол.

Если известны катет и гипотенуза в прямоугольном треугольнике:

P = √ c 2 — a 2 + (a + c), где a — любой катет, c — гипотенуза.

Гипотенуза — сторона, которая лежит напротив прямого угла.

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Видео:Найти периметр треугольника. Вневписанная окружностьСкачать

Треугольник вписанный в окружность

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Как вычислить периметр #геометрия #задача #треугольник #периметрСкачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:Задача 6 №27624 ЕГЭ по математике. Урок 71Скачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Периметры фигур. Периметр треугольника.

Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр

имеет ту же размерность величин, что и длина.

Треугольник — это многоугольник с тремя сторонами. Стороны треугольника обозначаются малыми

буквами, соответствующими обозначению противоположных вершин.

Периметр треугольника равен сумме длин его сторон, общая формула:

где a,b,c — длины сторон треугольника

Формула периметра треугольника для треугольника АВС:

Периметр равностороннего треугольника.

Чтобы найти периметр равностороннего треугольника (или найти периметр правильного

треугольника), нужно знать его сторону.

В общем случае для нахождения периметра треугольника используют формулу:

Поскольку в равностороннем треугольнике все три стороны равны, формула упрощается:

Таким образом, периметр равностороннего треугольника находится по такой формуле:

где а — длина его стороны.

Периметр равнобедренного треугольника.

Чтобы найти периметр равнобедренного треугольника, нужно знать всего две его стороны — основание

и боковую сторону.

Поскольку у равнобедренного треугольника две стороны равны (боковые), найти периметр

равнобедренного треугольника можно по такой формуле:

То есть, периметр равнобедренного треугольника равен сумме длин основания и

🎥 Видео

Площадь круга. Математика 6 класс.Скачать

КАК НАЙТИ ПЕРИМЕТР ТРЕУГОЛЬНИКА? Примеры | МАТЕМАТИКА 5 классСкачать

Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Урок. Как найти периметр треугольника. Математика 2 класс. #учусьсамСкачать

Что такое периметр. Как найти периметр многоугольника?Скачать

Длина окружности. Площадь круга - математика 6 классСкачать

№146. Отрезки АВ и CD — диаметры окружности с центром О. Найдите периметр треугольника AOD, еслиСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать