Угол abc лежит в плоскости a точка k не принадлежит плоскости a сколько прямых параллельных

Геометрия | 10 — 11 классы

Треугольник ABC лежит в плоскости а точка м не принадлежит плоскости а сколько прямых паралельных сторонам треугольника можно провести через точку м.

Так как через произвольную точку, не лежащую на прямой, можно провести единственную прямую, параллельную данной, то через точку М можно провести прямые, каждая из которых будет параллельна одной из сторон треугольника, то есть 3 прямые.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Какое из утверждений верно?

Какое из утверждений верно?

А) если две точки треугольника лежат в плоскости, то и весь треугольник лежит в плоскости ;

б) прямая, лежащая в плоскости треугольника пересекает его стороны ;

в) любые две плоскости имеют только одну общую точку ;

г) через две точки проходит плоскость, и притом только одна ;

д) прямая лежит в плоскости треугольника , если она пересекает две прямые, содержащие стороны треугольника.

Видео:Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

Прямые а и в пересекаются в точке О, точка А лежит в плоскости, точка В принадлежит прямой в, точка Р принадлежит прямой АВ?

Прямые а и в пересекаются в точке О, точка А лежит в плоскости, точка В принадлежит прямой в, точка Р принадлежит прямой АВ.

Докажите, что а и в и Р лежат в одной плоскости = ).

Видео:№34. Точка D не лежит в плоскости треугольника ABC, точки М, N и Р — середины отрезков DA, DBСкачать

1. Точки А и В принадлежат плоскости a(альфа), а точка С лежит вне плоскости а?

1. Точки А и В принадлежат плоскости a(альфа), а точка С лежит вне плоскости а.

Выберите правильное утверждение :

Прямая АС лежит в плоскости а

Прямая АВ леит вне плоскости а.

В. Прямая АВ лежит в плоскости а

Прямая СВ лежит в плоскости а

В пространстве дана произвольная прямая а и точка А.

Отметьте , какие из следующих четырех утверждений правильные, а какие не.

А. Через прямую а и точку А всегда можно провести плоскость.

Б. Если плоскость проходит через прямую а, то она обязательно содержит точку А.

В. если через прямую а и точку А можно провести только одну плоскость , то прямая а проходит через точку А

Если через прямую а и точку А можно провести две разные плоскости , то точка А лежит на прямой а.

Видео:Параллельность прямой к плоскостиСкачать

Решите срочно?

1. Прямая | имеет с пересекающимися прямыми а и b две общие точки.

Докажите, что эти три прямые расположены в одной плоскости.

2. точка М принадлежит медиане AD треугольника АВС.

Можно ли провести через точку М прямую, которая не пересекает сторон данного треугольника?

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Помогите пожалуйста, срочно надо?

Помогите пожалуйста, срочно надо!

1. Каково взаимное расположение прямых а и b, если известно, что через них можно провести : а) единственную плоскость ; б) несколько плоско­стей?

Выполните соответствующие чертежи.

2. Треугольники ABC и ABD расположены так, что точка С не лежит в плоскости ABD.

Точка Н — середина отрезка AD.

O — точка пересечения медиан треугольника А ВС.

Определите положение точки пе­ресечения прямой НО с плоскостью DBC.

3. Параллелограмм ABCD и треугольник ВСК расположены так, что точка K не принадлежит пло­скости ABC.

Точка О — точка пересечения диагона­лей ABCD.

Найдите линию пересечения плоскостей : a) ADK и ОСК ; б) BDK и АС К.

4. Прямая а и параллельная ей плоскость b не проходят через точку М.

Докажите, что через точку М проходит прямая, параллельная прямой а и плоскости b, и притом только одна.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Точка М принадлежит медиане AD треугольника ABC?

Точка М принадлежит медиане AD треугольника ABC.

Можно ли провести через точку М прямую, которая не пересекает сторон данного треугольника.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

1. Сколько различных плоскостей можно провести : а) через одну точку б) через две точки в) через три точки г) через четыре точки, любые три из которых не лежат на одной прямой?

1. Сколько различных плоскостей можно провести : а) через одну точку б) через две точки в) через три точки г) через четыре точки, любые три из которых не лежат на одной прямой?

2. Всегда ли прямая, которая пересекает две стороны треугольника(не проходящая через его вершины), лежит в плоскости треугольника?

3. Четыре точки не лежат в одной плоскости.

Могут ли какие нибудь три их них лежать на одной прямой?

Видео:№196. Дан треугольник ABC. Сколько прямых, параллельных стороне АВ, можно провестиСкачать

1. Прямая | имеет с пересекающимися прямыми а и b две общие точки?

1. Прямая | имеет с пересекающимися прямыми а и b две общие точки.

Докажите, что эти три прямые расположены в одной плоскости.

2. точка М принадлежит медиане AD треугольника АВС.

Можно ли провести через точку М прямую, которая не пересекает сторон данного треугольника?

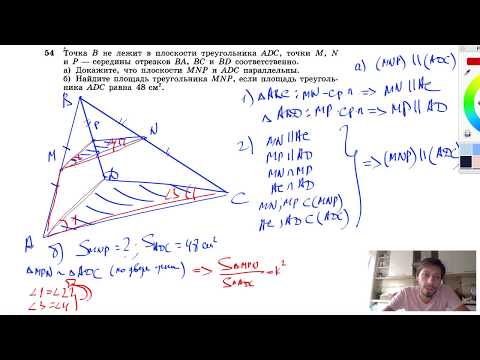
Видео:№54. Точка В не лежит в плоскости треугольника ADC, точки М, N и Р — середины отрезков ВА, ВССкачать

Можно ли через вершину треугольника провести прямую которая не лежит в его плоскости?

Можно ли через вершину треугольника провести прямую которая не лежит в его плоскости.

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Дан параллелограмм ABCD точка Е не лежит в плоскости BCD?

Дан параллелограмм ABCD точка Е не лежит в плоскости BCD.

Можно ли через прямую EA и точки В и С провести плоскость?

На этой странице вы найдете ответ на вопрос Треугольник ABC лежит в плоскости а точка м не принадлежит плоскости а сколько прямых паралельных сторонам треугольника можно провести через точку м?. Вопрос соответствует категории Геометрия и уровню подготовки учащихся 10 — 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

4) В треугольнике ВОС ОС = ОВ как радиусы окружности, значит он равнобедренный. ОВ = ОС, значит∠ОСВ = ∠ОВС = ∠1. ∠2 — внешний угол тр — ка ВОС, значит он равен сумме несмежных с ним углов. ∠2 = ∠ОВС + ∠ОСВ = 2∠1. Доказано. 8) Треугольники АОД и ..

Ответ на фото . Удачи ))).

Уточни, пожалуйста , что такое NE, EP. FE, EM.

Надеюсь, что ты поймёшь мой почерк и мое решение.

В мажорной хроматической гамме при движении вверх повышаются все ступени кроме третьей и шестой (вместо шестой понижается седьмая ступень). Мажорная хроматическая гамма от до1 вверх В мажорной хроматической гамме при движении вниз понижаются все сту..

За поиставка тих корень ш суффикс ие окончание.

Решение на фотографии.

Все) поставь пожалуйста ответ как лучший.

По формуле : S = (1 / 2)2 * 10 = 1 / 4 * 10 = 40 cm.

Это Пифагоров треугольник и гипотенуза АВ = 5. А можно и по простому — по Пифагору АВ = √(АС² + ВС²) = √(9 + 16) = 5. Ответ : АВ = 5.

Видео:Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Варианты заданий для проведения текущего контроля по УД «Математика» (1 курс, СПО, спец. Технология продукции общественного питания)

Видео:Следы прямой Взаимное положение двух прямыхСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

СТО СМК 4.2.01 — 2019

Государственное автономное профессиональное образовательное учреждение

«Чукотский многопрофильный колледж»

____________ / Паксюткина Е.А.

от «______»_______2019 г.

для проведения текущего контроля

по дисциплине ОУД.03. Математика

для студентов 1 курса

специальности 19.02.10 Технология продукции общественного питания

на заседании предметно-цикловой комиссии математических и естественнонаучных дисциплин

Протокол №__ от ______2019 г.

Председатель ______________/Глухарева Е.А.

Преподаватель ГАПОУ ЧАО «ЧМК» ___________/Ерёмин С.А.

Методист ПЦК _________________/Горелов В. С.

Рассмотрено на заседании ПЦК

___________/ Глухарева Е.А./

Перечень вариантов заданий

Подпись преподавателя ______ / Ерёмин С.А. /

«___» ___________ 2019 г.

Раздел 1. Алгебра

Тема 1.1. Развитие понятия о числе

1. Упростите выражение:

1)

2)

2. Выполните действия:

3. Найдите значение выражения:

1)

2)

3)

4)

5)

6)

7)

8) при

9) при

10) при

11) , если при

12) , если

13) , если

14) , если

15) , если

16) , если , а

17) , если

18) , если

19) , если

20) , если

4. Выясните, является ли геометрической прогрессией последовательность, заданная формулой n —го члена:

1)

2)

5. Выясните, является ли бесконечно убывающей геометрической прогрессией последовательность, заданная формулой n —го члена:

1)

2)

6. Найдите сумму бесконечно убывающей геометрической прогрессии:

1)

2)

3)

4)

5)

6)

Тема 1.2. Корни, степени и логарифмы

1. Представьте выражение в виде степени числа x ( x >0):

1)

2)

3)

4)

1)

2)

3)

4)

3. Упростите выражение:

1)

2)

3)

4)

5)

6)

4. Сравните числа:

1)

2)

3)

4)

5. Вынесите множитель из под знака корня ( x >0, y >0):

1)

2)

6. Внесите множитель под знак корня ( x >0):

1)

2)

7. Избавьтесь от иррациональности в знаменателе дроби:

1)

2)

3)

4)

8. Запишите данную зависимость в виде показательной функции:

1)

2)

3)

4)

5)

6)

7)

8)

9. Решите уравнение:

1)

2)

3)

4)

5)

6)

7)

8)

1)

2)

3)

4)

5)

6)

7)

8)

11. Найдите значение x , если:

1)

2)

3)

4)

12. Сравните числа:

1) и

2) и

3) и 0

4) и 0

13. Решите уравнение:

1)

2)

3)

4)

5)

6)

7)

8)

Раздел 2. Основы тригонометрии

Тема 2.1. Основные понятия тригонометрии

1) sin 17  cos 13  + cos 17  sin 13 

2) sin 9  cos 99  – sin 99  cos 9 

3)

4) sin 15  sin 15  – cos 15  cos 15 

5) sin 20  cos 50  – cos 20  sin 50 

6) cos 10  cos 35  – sin 35  sin 10 

7)

8) sin 22,5  sin 22,5  – cos 22,5  cos 2,5 

9) sin 10  cos20  + sin 20  cos 10 

10) cos 109  cos 49  + sin 109  sin 49 

11) sin 50  cos 20  – cos 50  sin 20 

12) cos 71  sin 11  – sin 71  cos 11 

13)

14)

15)

16)

17)

18)

19)

20)

Тема 2.2. Основные тригонометрические тождества

1. Зная значение одной функции угла  , найдите значения остальных тригонометрических функций этого угла:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

16)

17)

18)

19)

20)

Тема 2.3. Преобразования простейших тригонометрических выражений

1. Замените выражение ему равным:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

16)

17)

18)

19)

20)

21)

22)

23)

Тема 2.4. Простейшие тригонометрические уравнения

1. Решите уравнения:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

Раздел 3. Функции, их свойства и графики

Тема 3.1. Функции. Область определения и множество значений функции

1. Найдите область определения функции, заданной формулой:

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

16)

17)

18)

19)

20)

21)

2. Постройте график функции:

1)

2)

3)

4)

5)

6)

3. Определите, при каком значении x квадратичная функция принимает наибольшее (наименьшее) значение; найдите это значение:

1)

2)

3)

4)

Тема 3.2. Степенные, показательные, логарифмические и тригонометрические функции

1. Постройте график функции:

1)

2)

3)

4)

Раздел 4. Начала математического анализа

Тема 4.1. Последовательности

1. Вычислите пределы функций на бесконечности:

1)

2)

3)

4)

2. Вычислите пределы:

1)

2)

3)

4)

5)

6)

Тема 4.2. Производная

1. Найти производную в точке :

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

16)

17)

18)

19)

20)

Тема 4.3. Первообразная и интеграл

1. Найти площадь плоской фигуры, ограниченной линиями:

2. Найти объемы тел вращения, образованных вращением вокруг оси О x площадей, ограниченных линиями:

1) y 2 – 4 x = 0, x – 2 = 0, x – 4 = 0, y = 0

Раздел 5. Уравнения и неравенства

Тема 5.1. Уравнения и системы уравнений

1. Решите уравнение:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

2. Решите систему уравнений:

1)

2)

3)

4)

5)

6)

7)

8)

3. Решите систему уравнений:

1)

2)

3)

4)

4. Решите систему:

1)

2)

Тема 5.2. Неравенства

1. Решите неравенство:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

2. Решите неравенство:

1)

2)

3)

4)

5)

6)

7)

8)

3. Решите графически неравенство:

1)

2)

4. Решите систему:

1)

2)

3)

4)

5. Решите неравенство:

1)

2)

3)

4)

5)

6)

Раздел 6. Геометрия

Тема 6.1. Прямые и плоскости в пространстве

1. Угол ABC лежит в плоскости  , точка K не принадлежит плоскости  . Сколько прямых, параллельных сторонам угла, можно провести через точку K ?

2. Треугольник ABC лежит в плоскости  , точка M не принадлежит плоскости  . Сколько прямых, параллельных сторонам треугольника, можно провести через точку M ?

3. Точка M принадлежит ребру SB пирамиды SABC . Сколько прямых, параллельных ребрам, можно провести через точку M ?

4. Дан пространственный четырёхугольник АВСD, в котором диагонали АС и ВD равны. Середины сторон этого четырёхугольника соединены последовательно отрезками.

а) Выполните рисунок к задаче.

б) Докажите, что полученный четырёхугольник – ромб.

5. Прямые a и b лежат в параллельных плоскостях  и  . Могут ли эти прямые быть параллельными; скрещивающимися? Сделайте рисунок для каждого возможного случая.

6. Прямые a и b лежат в пересекающихся плоскостях  и  . Могут ли эти прямые быть параллельными; скрещивающимися? Сделайте рисунок для каждого возможного случая.

7. Точки K и L лежат на прямых P N и P М, пересекающих плоскость  в точках N и М; . Найдите расстояние между точками K и L .

8. Точки P и T являются серединами ребер LL ₁ и MM ₁ параллелепипеда KLMNK ₁ L ₁ M ₁ N ₁. Сколько плоскостей, содержащих грани параллелепипеда, параллельны прямой PT ?

9. Точки H и P принадлежат ребрам AA ₁ и DD ₁ куба A В CDA ₁ B ₁ C ₁ D ₁. Сколько существует прямых, содержащих ребра куба и скрещивающихся с прямой HP ?

10. В прямоугольном параллелепипеде A В CDA ₁ B ₁ C ₁ D ₁ угол В C ₁ B ₁ равен 65  . Найдите угол между прямыми C ₁ B и DD ₁.

11. На каком рисунке изображено сечение куба плоскостью PRT ?

12. В тетраэдре MNTP , , MN =3, MT =4, . Найдите площадь грани NTP .

13. Сумма трех измерений прямоугольного параллелепипеда A В CDA ₁ B ₁ C ₁ D ₁ равна 40, AB : AA ₁: AD =2:2:4. Найдите наибольшую из диагоналей параллелепипеда.

14. Через точку K на ребре AD тетраэдра DABC проведено сечение параллельно грани ABC . Площадь сечения равна 27, AK : KD =1:3. Найдите площадь грани ABC .

15. В треугольнике ABC , , отрезок BK – медиана треугольника, . Найдите угол между прямыми MK и AB .

1) 30 

1)

2)

3)

4)

17. Точка M – середина ребра CC ₁ куба A В CDA ₁ B ₁ C ₁ D ₁. Длине какого отрезка равно расстояние от точки M до плоскости ABB ₁.

1) CB ₁ D ₁

19. Точки A и B лежат, а точка C не лежит в плоскости  . Точки M и N – середины отрезков AB и BC , , AB =8, BN =5. Найдите расстояние от точки C до плоскости  .

20. Р ебро MC тетраэдра ABCM перпендикулярно к плоскости ABC , MC =12. В треугольнике ABC , , AB =18. Какие из следующих утверждений являются верными?

1) плоскость BCM перпендикулярна к плоскости ABC

2) расстояние от точки B до плоскости ACM равно 9

3) расстояние от точки M до прямой AB равно AM

4) котангенс угла между плоскостью ABC и плоскостью ACM равен 0,75

Тема 6.2. Координаты и векторы

21. Вершины куба A В CDA ₁ B ₁ C ₁ D ₁ имеют координаты: , , , .

б) Разложите по координатным векторам вектор .

22. Векторы и равны. Найдите координаты точки A , если , .

23. Даны векторы , . Найдите координаты вектора если .

Видео:№172. Катет АС прямоугольного треугольника ABC с прямым углом С лежит в плоскости α, а уголСкачать

24. Определите значения m и n , при которых векторы коллинеарны, если . Сравните длины и направления векторов .

25. Даны точки и .

а) Найдите координаты середины отрезка AB .

б) Найдите координаты точки C , если точка A – середина отрезка CB .

в) Найдите расстояние от точки A до плоскости Oxy .

26. Даны векторы . Найдите:

а)

б)

27. Докажите, что четырехугольник ABCD – параллелограмм, если , , .

28. Найдите угол между прямыми AB и CD , если , , ,.

29. Ребро куба ABCDA ₁ B ₁ C ₁ D ₁ равно 1. Найдите скалярное произведение векторов:

а) ; б) ; в) .

30. Найдите скалярное произведение векторов если:

Тема 6.3. Многогранники

31. Площади двух граней прямоугольного параллелепипеда равны 10 см 2 и 40 см 2 , а длина их общего бокового ребра – 5 см. Найдите объем параллелепипеда.

32. Площадь боковой поверхности правильной треугольной призмы равна 108 см 2 . Диагональ боковой грани наклонена к плоскости основания призмы под углом 45  . Найдите объем призмы.

33. Основание прямой призмы – прямоугольный треугольник с катетами 3 см и 4 см. Площадь полной поверхности призмы равна 120 см 2 . Найдите объем призмы.

34. Основание прямого параллелепипеда – ромб с периметром 20 см, диагонали которого относятся как 3:4. Объем параллелепипеда равен объему куба с ребром 6 см. Найдите высоту параллелепипеда.

35. Основание призмы – прямоугольный треугольник с катетами 6 см и 8 см. Боковое ребро призмы равно гипотенузе основания и образует с плоскостью основания угол 30  . Найдите объем призмы.

36. Сечение наклонного параллелепипеда, перпендикулярное к боковому ребру, является ромбом со стороной 4 дм и острым углом 60  . Найдите объем параллелепипеда, если его боковое ребро равно большей диагонали ромба.

37. Боковое ребро наклонного параллелепипеда равно 8 см. Сечение параллелепипеда, перпендикулярное к боковому ребру, является ромбом с тупым углом 120  , меньшая диагональ которого равна боковому ребру. Найдите объем параллелепипеда.

38. Сторона основания правильной треугольной пирамиды равна а . Боковое ребро образует с высотой пирамиды угол  . Найдите объем пирамиды.

39. Двугранный угол при основании правильной четырехугольной пирамиды равен  . Найдите объем пирамиды, если площадь ее основания равна S .

40. Одно из оснований усеченной пирамиды – прямоугольный треугольник с катетами 6 см и 8 см. Периметр второго основания равен 12 см. Найдите объем пирамиды, если ее высота равна 6 см.

Тема 6.4. Тела и поверхности вращения

41. Радиус цилиндра равен 10 см. Сечение, параллельное оси цилиндра и удаленное от нее на 8 см, имеет форму квадрата. Найдите площадь сечения.

42. Прямоугольник вращается вокруг одной из своих сторон, равной 5 см. Площадь боковой поверхности цилиндра, полученного при вращении, равна 100  см 2 . Найдите площадь прямоугольника.

43. Высота конуса равна 3 см. Найдите площадь осевого сечения конуса, если оно является прямоугольным треугольником.

44. Радиус основания конуса равен R . Концы хорды основания, стягивающей дугу в 120  , являются концами двух взаимно перпендикулярных образующих. Найдите площадь полной поверхности конуса.

45. Радиусы оснований усеченного конуса равны 3 см и 6 см, а высота равна 4 см. Найдите площадь осевого сечения боковой поверхности конуса.

46. Радиус большого основания, образующая и высота усеченного конуса равны 7 см, 5 см и 4 см соответственно. Найдите площадь осевого сечения боковой поверхности конуса.

47. Равнобочная трапеция с основаниями 4 см и 10 см и высотой 4 см вращается вокруг большого основания. Найдите площадь поверхности тела вращения.

48. Сфера задана уравнением .

а) Найдите координаты центра и радиус сферы

б) Определите, принадлежат ли данной сфере точки A и B , если, .

49. В шаре радиуса 13 см проведено сечение, площадь которого равна 25  см 2 . Найдите расстояние от центра шара до плоскости сечения.

50. К сфере площадью 144  см 2 проведена касательная плоскость, на которой выбрана точка А. Расстояние от точки А до наиболее удаленной от нее точки сферы равно 16 см. Найдите расстояние от точки А до точки касания сферы с плоскостью.

Тема 6.5. Измерения в геометрии

51. Осевое сечение конуса – равносторонний треугольник с высотой см. Найдите объем конуса.

52. Объем конуса равен 27  см 3 . Найдите площадь боковой поверхности конуса, если угол при вершине его осевого сечения равен 120  .

53. Радиусы оснований усеченного конуса равны 2 см и 8 см, а длины его высоты и образующей относятся как 4:5. Найдите объем конуса.

54. Периметр осевого сечения усеченного конуса равен 34 см. Найдите объем конуса, если его образующая равна 5 см, а радиусы оснований относятся как 1:2.

55. Объем шара равен 36  см 3 . Найдите площадь сферы, ограничивающей данный шар.

56. Найдите объем шарового сектора, если радиус шара равен 6 см, а высота конуса, образующего сектор составляет треть диаметра шара.

57. Радиус шара равен R , а угол между радиусами в осевом сечении шарового сегмента равен 120  . Найдите объем сектора.

58. Прямоугольный треугольник с катетом а и прилежащим острым углом  вращается вокруг гипотенузы. Найдите объем тела вращения.

59. Прямоугольный треугольник с гипотенузой с и острым углом  вращается вокруг гипотенузы. Найдите объем тела вращения.

60. Равнобочная трапеция с основаниями 4 см и 10 см и боковой стороной 5 см вращается вокруг большего основания. Найдите объем тела вращения.

Раздел 7. Элементы комбинаторики, теории вероятностей и математической статистики

Тема 7.1. Элементы комбинаторики

61. Сколькими способами можно составить расписание одного учебного дня из 5 различных уроков?

62. В 11«Б» классе 32 учащихся. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?

63. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?

64. Вычислить: 6! -5!

65. Вычислите:

66. Сколькими способами можно расставить 4 различные книги на книжной полке?

67. Сколько диагоналей имеет выпуклый семиугольник?

68. В футбольной команде 11 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами это можно сделать?

69. Сократите дробь:

70. Сколько существует трехзначных чисел, все цифры которых нечетные и различные.

Тема 7.2. Элементы теории вероятностей

71. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?

72. Вероятность того, что новый DVD-проигрыватель в течение года поступит в гарантийный ремонт, равна 0,045. В некотором городе из 1000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступила 51 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?

73. На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест.

74. На олимпиаде в вузе участников рассаживают по трём аудиториям. В первых двух по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 250 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории

75. В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.

76. Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?

77. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной?

78. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.

79. Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «А = сумма очков равна 5»?

80. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 10, но, не дойдя до отметки 1 час.

Тема 7.3. Элементы математической статистики

81. При проведении контроля качества среди 1000 случайно отобранных деталей оказалось 5 бракованных. Сколько бракованных деталей следует ожидать среди 25 000 деталей?

82. Включая в течение месяца телевизор около 150 раз, Вова в 30 случаях попадал на рекламу. Какой процент от времени телевизионных трансляций занимает реклама?

83. В Москве около 10 млн. жителей. Сколько жителей Москвы празднуют свой день рождения 1 января?

84. Комитет по проведению лотерей утверждает, что среди билетов лотереи «Спринт» половина выигрышных. Женя купил два билета лотереи и ничего не выиграл. Есть ли у Жени повод усомниться в честности её устроителей?

85. Экзамен по истории включает 60 вопросов. Вова утверждает, что подготовил 80% всех вопросов экзамена. Папа задал ему три вопроса, ни на один из которых он не ответил. Есть ли у папы основания подозревать сына во лжи?

86. Записан рост (в сантиметрах) пяти учащихся: 158, 166, 134, 130, 132. На сколько отличается средний рост этих учащихся (среднее арифметическое) от медианы?

87. Найдите частоту каждой из букв в строке «Октябрь уж наступил. » из стихотворения «Осень» А. С. Пушкина.

88. Найдите частоту (в процентах) букв слова «гром» среди всех букв двустишия «. Как бы резвяся и играя / Грохочет в небе голубом. » из стихотворения Ф. И. Тютчева.

89. Найдите моду и ее кратность среди всех букв двустишия «Это дерево сосна, / И судьба сосны ясна. » из стихотворения Ю. Минералова.

90. Измеряется длина слов в отрывке из поэмы А. С. Пушкина «Медный всадник». Составьте ряд данных и постройте гистограмму распределения этих данных.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

1. Точка К лежит в плоскости АВС. Постройте точку пересечения прямой. Геометрия 10 класс Зив Б.Г. Самостоятельная работа 1. Вариант 7

1. Точка К лежит в плоскости АВС. Постройте точку пересечения прямой DK и плоскости EFM (рис. 33).

ответ

1. Треугольник APD и трапеция ABCD имеют общую сторону AD и лежат в разных плоскостях. Через основание ВС трапеции и середину отрезка ( Подробнее. )

2.
Дано а ║α, а ║β, b ║ α, b║ β. Каково должно быть взаимное расположение данных прямых, чтобы плоскости а и β были параллельными? ( Подробнее. )

Say you are fond of both things.

Example: I am fond of both fruit and vegetables. ( Подробнее. )

Решите задачу:
За 3 ч мотоциклист проезжает то же расстояние, что велосипедист за 5 ч. Скорость мотоциклиста на 12 км/ч больше ( Подробнее. )

🔥 Видео

10 класс. Контрольная №3 (из 6). Тема: Перпендикулярность прямых и плоскости. Изучаем, решаем! :)Скачать

ВСЕ О СЕЧЕНИЯХ В СТЕРЕОМЕТРИИСкачать

Принадлежность прямой плоскостиСкачать

Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Точка, прямая и отрезок. 1 часть. 7 класс.Скачать

ЕГЭ №14. Задачи по стереометрии. 10-11 класс | Математика TutorOnlineСкачать