На клетчатой бумаге с размером 1х1 изображен четырехугольник найдите диагональ

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите длину его меньшей диагонали.

Проведем дополнительные построения, как показано на рисунке. Найдём длину диагонали по теореме Пифагора:

Задание некорректно: «Найдите длину меньшей диагонали» — у параллелограмма две диагонали и они равны.

У параллелограмма две диагонали. Но равны они только если параллелограмм — прямоугольник.

В условии сказано, что надо найти длину меньшей диагонали, но у параллелограмма диагонали равны.

У параллелограмма диагонали НЕ равны.

Задание некорректно. Во-первых, диагонали параллелограмма равны, а тут предлагается найти МЕНЬШУЮ диагональ. Во-вторых, если использовать свойство равенства диагоналей и попытаться найти диагональ AC, а потом ВD, то они не будут равны, а ребёнок впишет некорректный ответ. Хотя даже этого он сделать не сможет, так как АС равно корень из 200. Предлагаю заменить слово ПАРАЛЛЕЛОГРАММ на ЧЕТЫРЁХУГОЛЬНИК, тогда задание будет корректно.

Почему бы просто не найти длину меньшей диагонали параллелограмма? Получится 10, можно вписать в бланк.

Видео:Найдите площадь треугольника изображенного на клетчатой бумаге с размером клетки 1х1 см.Скачать

Геометрия. Применение формул. Задача 5 Базового ЕГЭ по математике

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

В этой статье — основные типы заданий №5 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований:

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где и — диагонали.

Получим:

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна

Площадь каждого из маленьких треугольников равна

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.

Значит, нам надо умножить площадь круга на . Получим:

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Видео:На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.Скачать

Презентация по математике на тему «Задача №4 ЕГЭ-2015 по математике, профильный уровень»

Видео:18 задание из ОГЭ. Найти диагональ квадратаСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Видео:На клетчатой бумаге с размером клетки 1 × 1 изображён ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Задача №4 ЕГЭ-2015 по математике, профильный уровень Учитель математики ГБОУ гимназии №1 города Похвистнево Самарской области Антонова Галина Васильевна http://linda6035.ucoz.ru/

Планиметрическая задача на нахождение геометрических величин (длин, углов, площадей). Задача №4 Задание на вычисление площади треугольника, четырёхугольника, круга и его частей, в том числе по данным рисунка, представляющего собой изображение фигуры, площадь которой требуется найти, на координатной плоскости или клетчатой бумаге (сетке) со стороной клетки 1⨯1. Тип задания Характеристика задания http://linda6035.ucoz.ru/

Задача №4 Площадь искомой фигуры может быть найден по известной формуле. Например, для треугольника или параллелограмма во многих случаях достаточно провести мысленно высоту к одной из сторон. Выбирать в качестве стороны и высоты нужно те, длины которых выражаются целым числом делений сетки, либо те, которые параллельны осям координат. В некоторых случаях для вычисления недостающих элементов можно использовать теорему Пифагора. Ряд задач можно решить, разбив фигуру на части, вычисление площадей которых не представляет труда, или заметив, что фигура сама является частью другой фигуры, а площадь последней можно найти почти сразу. Комментарий http://linda6035.ucoz.ru/

1. В треугольнике ABC CD — медиана, угол C равен 90°, угол B равен 35°. Найдите угол ACD. Ответ дайте в градусах. 2. Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. Задача №4 H Проведём высоту BH⊥ AC Ответ: 10 A C B http://linda6035.ucoz.ru/

3. Найдите площадь квадрата, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 4. В правильной четырёхугольной пирамиде SABCD с вершиной S точка O – центр основания, SO=35, SD=37. Найдите длину отрезка BD. Задача №4 A B C Ответ: 53 ABCD-квадрат, т.к. пирамида правильная, Ответ: 24 http://linda6035.ucoz.ru/

5. Площадь круга, изображённого на клетчатой бумаге, равна 16. Найдите площадь заштрихованного кругового сектора. Задача №4 Ответ: 6 Ответ: 8 http://linda6035.ucoz.ru/

7. В треугольнике ABC AC=BC, AB=14, AH — высота, BH=7. Найдите косинус угла BAC. Задача №4 14 7 Ответ: 0,5. • • • • Ответ: 12. H A B C http://linda6035.ucoz.ru/

9. В треугольнике ABC AD — биссектриса, угол C равен 104°, угол CAD равен 5°. Найдите угол B. Ответ дайте в градусах. 10. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AB. Задача №4 M N • • Ответ: 5 2 , http://linda6035.ucoz.ru/

11. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AB 12. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AB. Задача №4 • • M N Ответ: 5 H CH – высота к стороне AB и AB = 5. Ответ: 0 , 5 http://linda6035.ucoz.ru/

13. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AB. 14. На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции. A B C D Задача №4 H CH⊥AB, CH = 4 Ответ: M N Ответ: , 5 4 4 http://linda6035.ucoz.ru/

15. На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите его площадь. 16. На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите его площадь. Задача №4 Первый способ: О Второй способ: M A B C D A B D C Ответ: Ответ: http://linda6035.ucoz.ru/

17. Найдите площадь квадрата ABCD. Размер каждой клетки 1см⨯1см. Ответ дайте в квадратных сантиметрах. Задача №4 a H Ответ: 5 A B D C http://linda6035.ucoz.ru/

18. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AB. 19. На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции. Задача №4 A C D B • • • • M N M N H M,N-середины АС и ВС M,N-середины АС и ВD Ответ: Ответ: http://linda6035.ucoz.ru/

20. На клетчатой бумаге с размером клетки 1×1 отмечены точки A, B и C. Найдите расстояние от точки A до прямой BC. 21. На клетчатой бумаге с размером клетки 1×1 изображён равнобедренный прямоугольный треугольник. Найдите длину его медианы, проведённой к гипотенузе. Задача №4 • • • H B A C M M – середина AB, но в прямоугольном треугольнике медиана, проведённая к гипотенузе равна её половине: 5 , Ответ: Ответ: http://linda6035.ucoz.ru/

22. На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь. Задача №4 a = 3 h = 5 5 23. Найдите площадь трапеции, изображённой на рисунке. a = 4-2=2 b = 10-4=6 h=6-3=3 2 Ответ: Ответ: http://linda6035.ucoz.ru/

24. На клетчатой бумаге с размером клетки 1×1 изображён равнобедренный прямоугольный треугольник. Найдите длину его медианы, проведённой к гипотенузе. 25. На клетчатой бумаге с размером клетки 1×1 изображён равнобедренный прямоугольный треугольник. Найдите длину его биссектрисы, выходящей из вершины прямого угла. Задача №4 A B C A B C M , 5 Т.к. треугольник прямоугольный и равнобедренный, то биссектриса, выходящая из вершины прямого угла является и медианой, M , 5 Ответ: Ответ: http://linda6035.ucoz.ru/

26. Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (9;7), (7;7). a = 9 – 7 = 2 b = 10 – 1 = 9 h = 7 – 1 =8 4 Ответ: http://linda6035.ucoz.ru/

27. На клетчатой бумаге с размером клетки 1×1 отмечены точки A и B. Найдите длину отрезка AB. 28. На клетчатой бумаге с размером клетки 1×1 изображён угол. Найдите его градусную величину. Задача №4 H 0 С H М или 0 B A Ответ: Ответ: http://linda6035.ucoz.ru/

29. На клетчатой бумаге с размером клетки 1×1 изображён равнобедренный прямоугольный треугольник. Найдите радиус описанной около него окружности. 30. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AB. Задача №4 O B A C , 5 H Высота, опущенная на сторону AB – это отрезок CH и CH=5. Ответ: Ответ: http://linda6035.ucoz.ru/

32. Диаметр основания конуса равен 32, а длина образующей равна 65. Найдите высоту конуса. Задача №4 • • • • Ответ: O A S Ответ: 63 1 8 http://linda6035.ucoz.ru/

33. В треугольнике ABC AD — биссектриса, угол C равен 62°, угол CAD равен 31°. Найдите угол B. Ответ дайте в градусах. 34. Найдите площадь параллелограмма, изображённого на рисунке. Задача №4 a h Ответ: Ответ: 1 2 http://linda6035.ucoz.ru/

35. Найдите площадь четырёхугольника, изображённого на клетчатой бумаге с размером клетки 1см⨯1см (см. рисунок). Ответ дайте в квадратных сантиметрах. Ответ: Задача №4 3 0 http://linda6035.ucoz.ru/

36. Периметр треугольника ABC равен 8. Найдите периметр треугольника FDE, вершинами которого являются середины сторон треугольника ABC. Задача №4 Ответ: http://linda6035.ucoz.ru/

37. Площадь треугольника ABC равна 24. DE – средняя линия. Найдите площадь трапеции ABDE. H Задача №4 C Ответ: http://linda6035.ucoz.ru/

D F E C B A 38. Средняя линия трапеции равна 18, а меньшее основание равно 10. Найдите большее основание трапеции. 18 10 Средняя линия трапеции параллельна основаниям и равна их полусумме, т.е. 2 Задача №4 Ответ: http://linda6035.ucoz.ru/

39. Найдите площадь четырёхугольника, изображённого на клетчатой бумаге с размером клетки 1см⨯1см (см. рисунок). Ответ дайте в квадратных сантиметрах. 1 Задача №4 Ответ: http://linda6035.ucoz.ru/

40. Найдите площадь трапеции, изображённой на клетчатой бумаге с размером клетки 1см⨯1см (см. рисунок). Ответ дайте в квадратных сантиметрах. a =3 b =7 h = 5 2 Задача №4 Ответ: http://linda6035.ucoz.ru/

41. На клетчатой бумаге с размером клеток 1см⨯1см изображён четырёхугольник ABCD. Найдите диагональ BD. H Задача №4 Ответ: http://linda6035.ucoz.ru/

42. На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите радиус описанной около него окружности. Диаметр окружности равен стороне зелёного квадрата, следовательно a = 7 Задача №4 , 3 Ответ: http://linda6035.ucoz.ru/

Задача №4 Использованные
http://reshuege.ru/ Подготовка к ЕГЭ по математике в 2015 году. Базовый и профильный уровни. Методические указания / И.В.Ященко, С.А.Шестаков, А.С.Трепалин. – М.: МЦНМО, 2015. ЕГЭ. Математика: типовые экзаменационные варианты: 36 вариантов / под ред. И.В.Ященко. – М. : Издательство «Национальное образование», 2015. Источник шаблона: Фокина Лидия Петровна, учитель начальных классов МКОУ «СОШ ст. Евсино» Искитимского района Новосибирской области, сайт http://linda6035.ucoz.ru/ http://linda6035.ucoz.ru/

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 973 человека из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 696 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 333 человека из 71 региона

Ищем педагогов в команду «Инфоурок»

В презентации приведены текст и решение 42 задач задачи №4 теста ЕГЭ-2015 по математике профильного уровня. Материал пригодится как для обучения учителем решению этих задач, так и для самостоятельной подготовки выпускников к итоговой аттестации. Приводится описание типа и характеристики задания, есть комментарии по решению такого типа задач. Решение каждой задачи анимировано с целью разъяснения хода решения задачи. Использованы задачи из открытого банка заданий сайтов ФИПИ ,»Решу ЕГЭ» и типовых экзаменационных вариантов под редакцией И.В.Ященко издательства «Национальное образование».

• Антонова Галина ВасильевнаНаписать 8181 01.02.2015

Номер материала: 356138

01.02.2015 622

01.02.2015 620

01.02.2015 549

01.02.2015 1636

01.02.2015 2919

01.02.2015 808

01.02.2015 450

Не нашли то, что искали?

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минпросвещения готовит рекомендации по построению «идеальной школы»

Время чтения: 1 минута

Число участников РДШ за 2021 год выросло в три раза

Время чтения: 2 минуты

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

Глава СПЧ предложил ввести подготовительные курсы перед обучением в школе для детей мигрантов

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🎬 Видео

На клетчатой бумаге с размером клетки 1 × 1 изображён ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

ОГЭ по математике На клетчатой бумаге с размером 1х1 изображен параллелограммСкачать

На клетчатой бумаге с размером клетки 1 × 1 изображена ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

Самый простой способ нахождения площадиСкачать

ОГЭ ЗАДАНИЕ 18 ПЛОЩАДЬ РОМБА #математика #2023 #огэ #огэпоматематикеСкачать

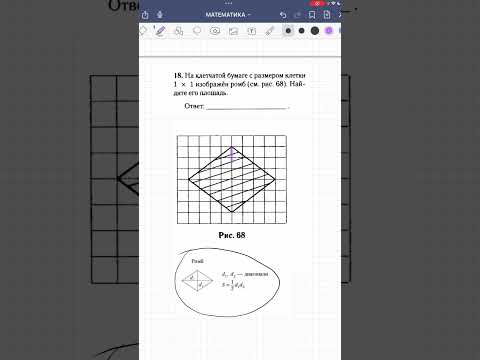
Задача 3 ЕГЭ по математике. Урок 13Скачать

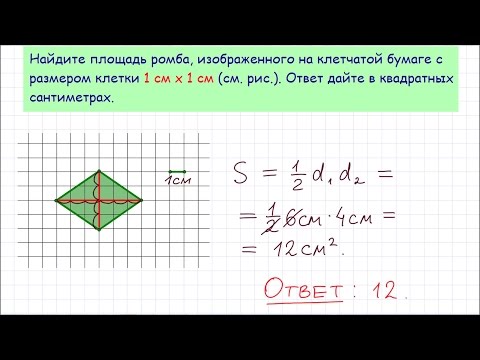
КОВАРНОЕ 18 ЗАДАНИЕ ОГЭСкачать

Вариант 2 Задание 3 ЕГЭ 2016 Математика, И В Ященко 36 вариантов Решение ОтветСкачать

ОГЭ, математика, задание 18| Треугольник на клетчатой бумагеСкачать

Площадь ромба. Легче понять...Скачать

18 ЗАДАНИЕ ОГЭ НАЙДИТЕ ПЛОЩАДЬ ТРАПЕЦИИСкачать

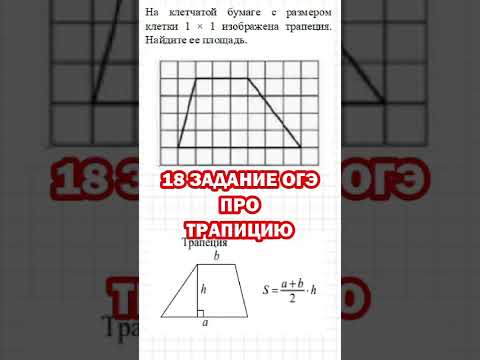
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.Скачать

На клетчатой бумаге с размером клетки 1 × 1 изображён ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

18 ЗАДАНИЕ ОГЭ НАЙТИ ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММАСкачать

САМОЕ БЫСТРОЕ И ПОНЯТНОЕ РЕШЕНИЕ. На клетчатой бумаге с размером клетки 1×1 изображён параллелограммСкачать

Самое трудное задание из пробника ОГЭ от ФИПИСкачать