Как строить образ треугольника

О чем эта статья:

Видео:Осевая симметрия, как начертить треугольники симметричноСкачать

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

• Ось симметрии угла — биссектриса.
• Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
• Оси симметрии прямоугольника проходят через середины его сторон.
• У ромба две оси симметрии — прямые, содержащие его диагонали.
• У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
• Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Видео:Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

1. Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
2. Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
3. С другой стороны прямой отложим такие же расстояния.
4. Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
5. Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

1. Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
2. Измеряем расстояние от вершин до точек на прямой.
3. Откладываем такие же расстояния на другой стороне оси симметрии.
4. Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

1. Проводим через точку А прямую, перпендикулярную прямой l.
2. Проводим через точку В прямую, перпендикулярную прямой l.
3. Измеряем расстояния от точек А и В до прямой l.
4. Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
5. Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Видео:Построение высоты в треугольникеСкачать

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

1. Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
2. Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
3. Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
4. Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

1. Измеряем расстояние от точки B до точки О и от точки А до точки О.
2. Проводим прямую из точки А через точку О и выводим ее на другую сторону.
3. Проводим прямую из точки B через точку О и выводим ее на другую сторону.
4. Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.
5. Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Видео:Строим треугольник по трем сторонам (Задача 5).Скачать

Построение треугольников. Задачи на построение

Вы будете перенаправлены на Автор24

Решение задач на построение состоит из четырех основных этапов:

Каждый этап является важным. Например, анализ и исследование задачи необходимы для рассмотрения случаев, когда задача будет иметь решение, а когда – нет.

Построение фигур проще выполнять с помощью транспортира и линейки с делениями, но в математике необходимо уметь выполнять построение, используя циркуль и линейку без делений.

Видео:Построение медианы в треугольникеСкачать

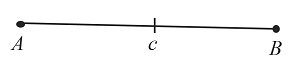
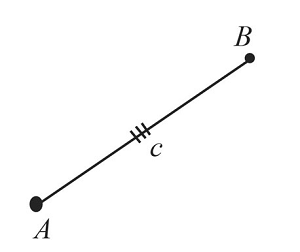
Построение отрезка, равного заданному

Построить отрезок, равный заданному, можно за 3 действия. Каждое действие обозначено на рисунке соответствующими цифрами.

Пусть необходимо построить отрезок, который будет равен отрезку $АВ$. Для этого:

1. Отметим произвольно точку $А_1$ и проведем луч с началом в этой точке.
2. С помощью циркуля измерим заданный отрезок $АВ$.
3. Проведем часть окружности с радиусом, равным отрезку $АВ$, и центром в точке $А_1$. В точке пересечения окружности и построенного луча получим точку $В_1$.

Таким образом, построенный отрезок $А_1 В_1$ будет равен заданному отрезку $АВ$.

Видео:Построение треугольника, равного данномуСкачать

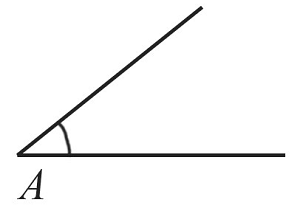
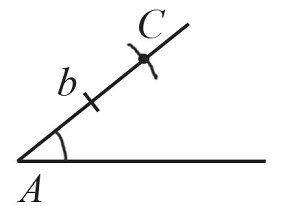
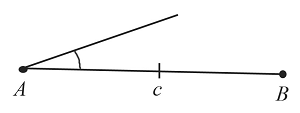
Построение угла, равного заданному

Построить угол, равный заданному, можно за $5$ действий. Каждое действие обозначено на рисунке соответствующими цифрами.

Пусть необходимо построить угол, который будет равен углу $А$.

1. Отметим произвольную точку $А_1$ и проведем из нее луч $А_1$.
2. Циркулем с произвольным радиусом проведем часть окружности с центром в точке $А$ до пересечения обеих сторон заданного угла $А$.
3. С тем же радиусом проведем часть окружности с центром в точке $А_1$ до пересечения с лучом $А_1$.
4. Из точек пересечения проведем окружности с одинаковым радиусом.
5. Проведем прямую из точки $А_1$ через вторую точку пересечения.

Готовые работы на аналогичную тему

Видео:Построение биссектрисы в треугольникеСкачать

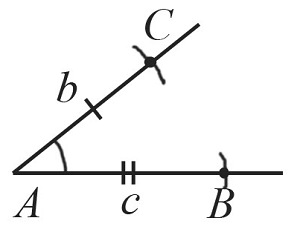
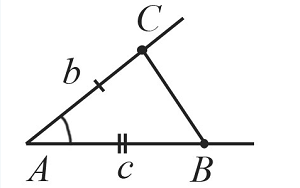
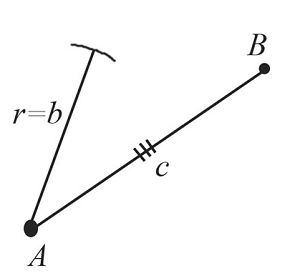
Построение треугольника по двум сторонам и углу между ними

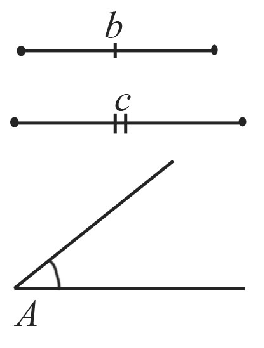
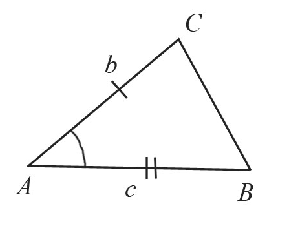
Пусть даны два отрезка $b$ и $с$ и угол $А$:

Необходимо построить треугольник с заданными двумя сторонами и углом между ними:

Построение выполняется в 4 этапа, каждый из которых показан на рисунках:

Построим угол $А$, который равен заданному углу по схеме, которая рассматривалась выше.

С помощью циркуля замеряем отрезок $b$ и отложим от точки $А$ такой же отрезок на одной из сторон построенного угла. Получим точку $С$.

Циркулем замеряем отрезок $с$ и отложим от точки $А$ такой же отрезок на второй стороне построенного угла. Получим точку $В$.

С помощью линейки соединим точки $В$ и $С$.

Таким образом, получили треугольник $АВС$, построенный по двум сторонам и углу между ними.

Для облегчения построения полезно схематически изобразить будущий треугольник со всеми необходимыми элементами. Так будет наглядней видно, что после чего нужно строить.

Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

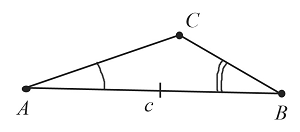
Построение треугольника по стороне и прилегающим к ней углам

Пусть даны два угла $А$ и $В$ и отрезок $с$:

Необходимо построить треугольник с заданными двумя углами и стороной, к которой они прилегают:

Построение выполняется в $3$ этапа, каждый из которых показан на рисунках:

Начертим произвольный отрезок $АВ$, который равен заданному отрезку $c$.

Построим угол $А$, который равен заданному, как показано выше.

Построим угол $В$, который равен заданному.

Точка пересечения двух сторон построенных углов $А$ и $В$ является вершиной треугольника $С$.

Таким образом, получили треугольник $АВС$, построенный по стороне и двум углам.

Видео:Поворот фигуры. Построить поворот фигур вокруг точки на угол по часовой или против часовой стрелкиСкачать

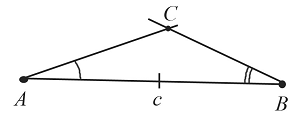
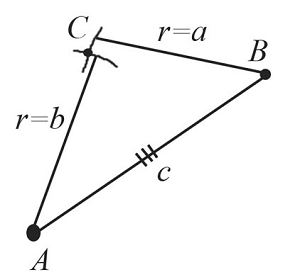
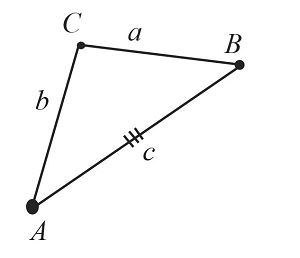
Построение треугольника по трем сторонам

Пусть даны $3$ отрезка $а$, $b$ и $с$.

Необходимо построить треугольник по трем заданным сторонам.

Построим отрезок $АВ$, который равен заданному отрезку $c$.

Из точки $А$ проведем часть окружности с радиусом, равным заданному отрезку $b$.

Из точки $В$ проведем часть окружности с радиусом, равным заданному отрезку $a$. Пересечением обеих окружностей является точка $С$.

Таким образом, получили построенный треугольник $АВС$ по трем заданным сторонам.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 22 07 2021

Видео:Построение треугольника в трёх проекцияхСкачать

Как построить треугольник равный данному треугольнику?

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

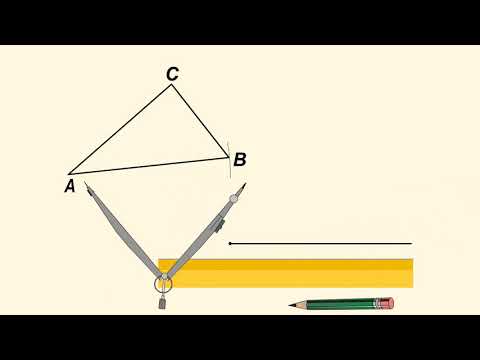
Как строить треугольник по 3 сторонам?

построение треугольника по трём сторонам.

1. Провести прямую.
2. На прямой от выбранной точки A отложить отрезок, равный данному отрезку a, и отметить другой конец отрезка B.
3. Провести окружность с центром A и радиусом, равным отрезку b.
4. Провести окружность с центром B и радиусом, равным отрезку c.

Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

Как построить угол равный данному?

Чтобы построить угол равный данному, проводим прямую и ставим на ней точку. Это будет вершина нашего угла. Берем циркуль с произвольным раствором, ставим его на вершину данного угла. Проводим дугу таким образом, чтобы она пересекла лучи данного угла.

Видео:Геометрия 9 класс (Урок№29 - Параллельный перенос.)Скачать

Можно ли построить треугольник по двум сторонам и медиане?

Отрезок, соединяющий вершину с серединой противоположной стороны, называют медианой. Зная длины двух сторон и медианы, соединяющихся в одной из вершин, можно построить треугольник, не имея данных о длине третьей стороны или величинах углов.

Видео:Построения с помощью циркуля и линейки. Равнобедренный и равносторонний треугольникиСкачать

Как построить прямоугольный треугольник по гипотенузе и катету?

По катету и гипотенузе прямоугольный треугольник можно построить как минимум двумя способами. Способ 1: Начертить прямую и отложить на ней меньший отрезок (обозначим его как AB). Для построения перпендикулярной прямой отложить такой же отрезок по другую сторону одной из точек концов отрезка, отложенного в п.

Видео:№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Когда равны прямоугольные треугольники?

По гипотенузе и катету: если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Видео:Построить описанную окружность (Задача 1)Скачать

Как начертить отрезок с помощью циркуля и линейки?

Одно из решений показано на рисунке:

1. Циркулем проводим окружности с центром в точках A и B радиусом AB.
2. Находим точки пересечения P и Q двух построенных окружностей (дуг).
3. По линейке проводим отрезок или линию, проходящую через точки P и Q.
4. Находим искомую середину отрезка AB — точку пересечения AB и PQ.

Видео:Медиана, высота и биссектриса треугольника. Центроид, инцентр, ортоцентр. Геометрия 7 класс.Скачать

Как построить середину данного отрезка?

Для нахождения середины отрезка на плоскости можно сначала построить две дуги равного (и достаточно большого) радиуса с центрами в концах отрезка, а затем через точки пересечения этих дуг провести прямую. Точка, где полученная прямая пересекает отрезок, является его серединой.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Как рассчитать градус треугольника?

Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.

Видео:Параллельный перенос. Симметрия. Поворот | МатематикаСкачать

Как сделать правильный треугольник?

Циркуль Проведите прямую линию. На лист бумаги положите линейку и проведите карандашом вдоль длинной стороны линейки. Полученный отрезок является первой стороной равностороннего треугольника, то есть вам нужно нарисовать еще две стороны той же длины, а каждый угол между сторонами должен быть равен 60 градусам.

Как при помощи циркуля построить треугольник?

Построение правильного треугольника. Способ 1

1. Как построить равносторонний треугольник с помощью циркуля Шаг 1. Проведите отрезок АВ, длина которого равна а. .
2. Шаг 2. Возьмите циркуль. .
3. Шаг 3. Теперь неподвижную часть циркуля поставьте в точку В, а подвижную в точку А. .
4. Шаг 4. Окружности пересекаются в двух точках.