Теорема симпсона для треугольника

Инструменты пользователя

Инструменты сайта

Боковая панель

Навигация

Загрузки всякие

Связь

Содержание

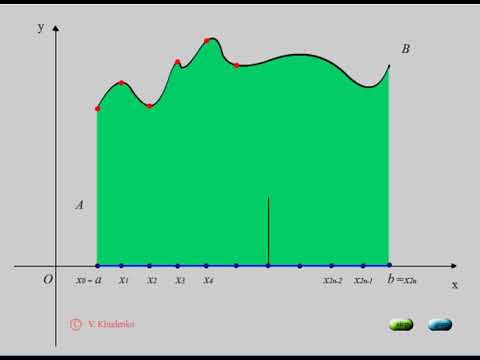
Видео:Метод СимпсонаСкачать

Прямая Симсона

Прямая Симсона — прямая, связанная с треугольником.

Точки, лежащие на одной прямой, называют коллинеарными . Две точки всегда коллинеарны.

Эта теорема дает красивый критерий коллинеарности трех точек.

Основания перпендикуляров, опущенных из точки $P$ описанной окружности треугольника $ABC$ на его стороны или их продолжения, лежат на одной прямой. Эта прямая называется прямой Симсона.

Проекции точки $P$ описанной окружности треугольника $ABC$ на его стороны, лежат на одной прямой.

Открытие этой прямой долго приписывалось Роберту Симсону (1687—1768), но в действительности она была открыта лишь в 1797 году шотландским математиком Уильямом Уоллесом. Поэтому наряду с традиционным названием этой прямой часто используется исторически более справедливое название прямая Уоллеса.

Если точка P и точка B — концы диаметра, то AC — прямая Симсона

Утверждение

Пусть H — ортоцентр треугольника. Тогда прямая Симсона произвольной точки P делит отрезок PH пополам. (решение Прасолов) Эта середина лежит на окружности 9 точек.

Видео:Формула СимпсонаСкачать

Свойства

Верно и обратное утверждение: если основания перпендикуляров, опущенные из произвольной точки плоскости $P$ на стороны треугольника $ABC$ или их продолжения, лежат на одной прямой, то точка $P$ лежит на описанной окружности треугольника.

Пусть $H$ — ортоцентр треугольника $ABC$. Тогда прямая Симсона произвольной точки $P$ делит отрезок $PH$ пополам.

Существуют обобщения прямой Симсона. Если из данной точки $P$ описанной окружности треугольника $ABC$ провести прямые под данным ориентированным углом к сторонам, то три полученных точки пересечения будут лежать на одной прямой.

Прямую Симсона можно определить для любого вписанного n-угольника по индукции следующим образом: прямой Симсона точки P относительно данного n-угольника назовем прямую, содержащую проекции точки P на прямые Симсона всех (n-1)-угольников, полученных выбрасыванием одной вершины n-угольника.

Прямые Симсона диаметрально противоположных точек описанной окружности перпендикулярны.

Видео:Формула СимпсонаСкачать

Педальный треугольник

Поде́рный или педальный треугольник (а также треугольник проекций) точки P относительно $triangle ABC$ — это треугольник, вершинами которого являются основания перпендикуляров, опущенных из точки P на стороны треугольника $ABC$ (или их продолжения).

Описанную окружность подерного треугольника называют подерной или педальной окружностью.

Подерный треугольник точки P вырождается в прямую тогда и только тогда, когда P находится на описанной окружности треугольника ABC . В этом случае прямая, содержащая подерный треугольник, называется прямой Симсона.

Теорема (прямая): Вершины подерного треугольника разделяют три стороны исходного треугольника на шесть отрезков так, что сумма квадратов трех из них, не имеющих общих концов, равна сумме квадратов трех других, также не имеющих общих концов.

Видео:16. Формула Симпсона ( практический курс по сопромату )Скачать

Прямая Симсона.

Теорема.

Основания перпендикуляров, опущенных из точки описанной окружности треугольника на его стороны или их продолжения, лежат на одной прямой.

Эта прямая называется прямой Симсона.

Доказательство.

Четырехугольник AEFD — вписанный в окружность с диаметром AD, так как ∠AED=∠AFD=90°. Следовательно, ∠AFE=∠ADE.

Четырехугольник DFCG — вписанный, так как ∠DFC+∠DGC=180°. Следовательно, ∠CFG=∠CDG.

∠BAD+∠DCB=180° (свойство вписанного четырехугольника ABCD).

∠DCG=180°-∠DCB (свойство смежных углов).

90°-∠CFG =90°-∠CDG= ∠DCG=∠EAD =90°-∠ADE= 90°-∠AFE.

Итак, ∠CFG=∠AFE. Следовательно, E, F, G лежат на одной прямой.

Видео:✓ Прямая Симсона в остроугольном треугольнике | В интернете опять кто-то неправ #011 | Борис ТрушинСкачать

репетитор по математике и физике

Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Артём Александрович Рогов

Челябинская область, г.Снежинск, на берегу озера Синара

Существуют в геометрии факты, которые не принято рассматривать в стандартном курсе геометрии. Хотя они просты и помогают в решении многих задач геометрии и поэтому их полезно знать учащимся, которые

хотят набрать высокий бал на ЕГЭ. Эти вопросы я подробно разбираю в своём специализированном курсе “ЕГЭ на сто”. Его я припадаю в двух формах: индивидуальные занятия и on-line с помощью ICQ или Skype.

Здесь я рассмотрю некоторые темы этого курса. Все вопросы мне можно прислать на e-mail: arogov_84@mail.ru

Я с удовольствием отвечу.

Замечание: поскольку все теоремы ниже не входят в стандарт общеобразовательной школы, то при их использовании в решении задач нужно их доказывать

Будем называть отрезок чевианной треугольника, если он соединяет вершину с противоположной стороной

Теорема Чевы. Пусть дан треугольник ABC и проведены три его чевианы AX BY CZ, пересекающиеся в точке P. Тогда справедливо утверждение

Как следует из рисунка

Аналогично для ;

Таким образом, получаем

Пусть дан треугольник ABC, R-радиус описанной окружности, r— вписанной окружности. Тогда расстояние между центрами вписанной и описанной окружности равны

Эта формула называется формулой Эйлера. Её проще всего получить если воспользоваться школьной теоремой о том, что при пересечение двух хорд, точка пересечения хорд делит их на отрезки произведение которых одной хорды равны произведению другой хорды. То есть рассмотрим две хорды AB и СD, а одна из которых проходит через диаметр(AB).

Пусть точка P-пересечение этих хорд лежит на расстоянии d от центра тогда по упомянутой выше теореме (*)

Теперь получим формулу Эйлера.

Рассмотрим треугольник ABC(см.рис.).

Пусть точка O-центр описанной окружности, I-центр вписанной окружности.

Тогда используя (*) имеем

Прямая Эйлера. Окружность Эйлера

Рассмотрим треугольник ABC. Пусть H-его ортоцентр, С’, A’,B’-середины его сторон AB, BC,CA, соответственно; K,M,L- середины отрезков BH,CH,AH, соответственно.

Сказанное проиллюстрировано на рисунке ниже

Теорема. Точки F,C’,K,E,A’,M,B’,D,L лежат на одной окружности Эйлера (она же окружность девяти точек, окружность Фейрбаха)

Прямая KM параллельна CB(средняя линия треугольника CHB)

Прямая B’C’ параллельна CB(средняя линия треугольника ABC)

Причём поскольку ВСAE и C’K параллельна AE(почему?), то четырехугольник C’KMB’-прямоугольник

Строим окружность с диаметром KB’. Точки С’ и M будут лежат на этой окружности так как они вершины прямоугольника C’KMB’

Точка D принадлежит этой окружности так как

Точка L принадлежит этой окружности так как четырёхугольник KLA’B’-прямоугольник(почему?). Значит A’ тоже лежит на этой окружности

Точки F и E также лежат на этой окружности(почему). То есть все девять точек принадлежат одной окружности. Теорема доказана

Теорема. Центройд треугольника(точка пересечения медиан, или центр тяжести треугольника лежит), ортоцентр, центр описанной окружности и центр окружности Эйлера лежат на одной прямой (прямая Эйлера)

Эффектное доказательство этого факта основано на применение гомотетии. По свойству точки пересечения медиан можем заключить, что гомотетичен с коэффициентом k= 0.5. тогда ортоцентр преобразуется в ортоцентр (точка пересечения срединных перпендикуляров ). Таким образом, ортоцентр , центр описанной возле него окружности и центр окружности Эйлера лежат на одной прямой.

Теорема. Радиус окружности Эйлера равен половине радиуса описанной окружности.

Утверждение легко следует из доказанной выше теоремы

Теорема Фейрбаха. Окружность Эйлера касается его трёх его вневписанных и вписанной окружности

Теорема. Пусть дан треугольник ABC и описанная возле него окружность. Из точки, лежащей на окружности проведём перпендикуляры пересекающиеся со сторонами треугольника в точках X,Y,Z. Тогда все три точки лежат на одной прямой(прямой Симпсона)

Докажем, что угол . В самом деле, (A,B,P,C лежат на одной окружности. Почему?)

(X,P,Z,A лежат на одной окружности. Почему?)

Таким образом, . Следовательно, (*).

Далее, поскольку точкиY,P,Z,Cлежат на одной окружности(?), то

Аналогично, (**). Тогда из (*) и (**). Отсюда следует, что Z,Y,X лежат на одной прямой.

Определение. Три точки коллинеарные, если они принадлежат одной прямой)

Пусть дан треугольник ABC и прямая пересекающая три его стороны в точках X, Y, Z(см.рис.). Тогда, если X,Y,Z лежат на одной прямой, то верно утверждение

(верно и обратное утверждение. Предлагаю сформулировать его и доказать самостоятельно)

Пусть дано, что X,Y,Z коллинеарные. Докажем

По определению гомотетии имеем (*)

По определению гомотетии имеем (**)

По определению гомотетии имеем (***)

Таким образом, гомотетию (**) можно представить как композицию (*) и (***)

Тогда точки , , лежат на одной прямой

Докажите этот факт самостоятельно. Разглядите на рисунке подходящие треугольники и примените к ним теорему Менелая.

теорема Дезарга(очень красивая теорема. начало проективной геометрии)

Пусть даны два и , таких что прямые , , пересекаются в точке S. Тогда если существуют точки

и , то они лежат на одной прямой(см.рис.)

Доказательство этой теоремы простое, но громоздкое и основано на теореме Менелая

🎥 Видео

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Теорема, обратная теореме Уоллеса-СимсонаСкачать

Прямая СимсонаСкачать

Педальный треугольникСкачать

Треугольник ПаскаляСкачать

9 класс, 12 урок, Теорема о площади треугольникаСкачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Интеграл Мора 3 Формулы Симпсона и трапецийСкачать

Метод прямоугольников для нахождения определенного интегралаСкачать

Теорема о биссектрисе угла треугольника | Осторожно, спойлер! | Борис Трушин |Скачать

Теорема Птолемей, прямая СимсонаСкачать

Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать

7 класс, 33 урок, Теорема о соотношениях между сторонами и углами треугольникаСкачать

Численное интегрирование: Методы Левых Правых прямоугольников, Трапеций, Симпсона c++Скачать