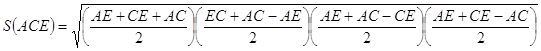Можно ли провести параллельные плоскости через две скрещивающиеся прямые d и c выберите ответ (2 видео)

Докажите, что через две скрещивающиеся прямые можно провести параллельные плоскости (рис. 36)

2.14. Докажите, что через две скрещивающиеся прямые можно провести параллельные плоскости (рис. 36).

Решение: Пусть прямые а и b скрещиваются. Выберем на прямой а произвольно точку А и проведем прямую с, параллельную b (через точку, не лежащую на данной прямой можно провести единственную прямую, параллельную данной). Прямые а и с задают плоскость β. По признаку параллельности прямой и плоскости: b || β. Аналогично, проведем прямую d в плоскости α.

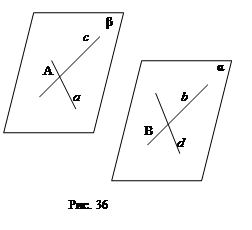
α || β (если две пересекающиеся прямые плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны).

3.06. Постройте сечение пятиугольной пирамиды PABCDE плоскостью α, которая проходит через внутреннюю точку М основания ABCDE параллельно грани РAB (рис. 37).

Решение: Так как прямые, по которым две параллельные плоскости пересечены третьей плоскостью, параллельны, а плоскость α параллельна грани РАВ, то: а) прямая пересечения плоскости α с плоскостью основания пирамиды должна быть параллельна АВ; б) прямая пересечения α с плоскостью грани РВС – параллельна АР; в) прямая пересечения α с плоскостью РАD – параллельна РА, поэтому проводим: 1) через точку М прямую KF || AB; 2) FH || PA; 3) KR || PB; 4) ML || AP. Пятиугольник HLRKF – искомое сечение. В доказательстве используется признак параллельности прямой и плоскости, признак параллельности плоскостей.

3.07. Точки А, В и С лежат в плоскости α и не лежат на одной прямой. Равные и параллельные отрезки АА₁, ВВ₁ и СС₁ расположены по одну сторону от плоскости α. Докажите, что (А₁В₁С₁) || 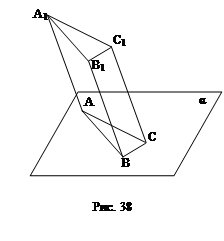(АВС) (рис. 38).

Решение: ВВ₁С₁С – параллелограмм (из параллельности и равенства ВВ₁ и СС₁), следовательно ВС || В₁С₁. АВ || А₁В₁ (аналогично). По теореме о параллельности плоскостей (по двум пересекающимся прямым): (А₁В₁С₁) || (АВС).

3.08. Точка В не лежит в плоскости ΔAEC, точки М, К и Р – середины отрезков соответственно АВ, ВС и ВЕ (рис.39). а) Докажите, что плоскости МКР и АЕС параллельны. б) Найдите площадь ΔМКР, если площадь ΔAEC равна 48 см 2 .

Решение: а)Заметим, что ΔAEC и не лежащая в нем точка В образуют тетраэдр ВАСЕ. МК || АС (МК – средняя линия ΔAВC). КР || СЕ (КР – средняя линия ΔВCЕ). По теореме о параллельности плоскостей (через пересекающиеся прямые): (МКР)||(АСЕ).

б) По формуле Герона:

, как средние линии соответствующих треугольников. Подставим данные значения в формулу: . Отсюда .

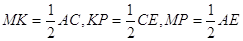
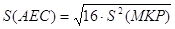
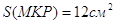
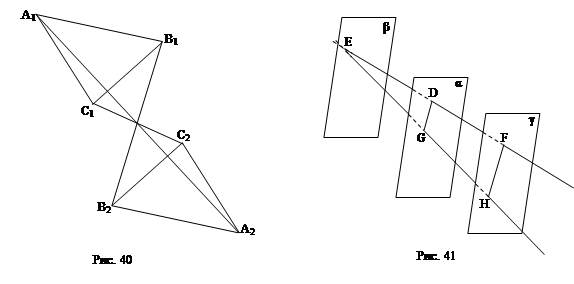
3.09. Три отрезка А₁А₂, В₁В₂ и С₁С₂, не лежащие в одной плоскости, имеют общую середину. Докажите, что плоскости А₁В₁С₁ и А₂В₂С₂ параллельны (рис. 40).

Решение: Каждые две пересекающиеся прямые задают плоскость (через любые две пересекающиеся прямые можно провести плоскость, и притом только одну). Так как точка пересечения делит прямые пополам, то по теореме Фалеса: А₁В₁ || В₂А₂. Аналогично доказывается параллельность С₁В₁ и С₂В₂, А₁В₁ и А₂В₂. По теореме о параллельности плоскостей (через пересекающиеся прямые): (А₁В₁С₁)||(А₂В₂С₂).

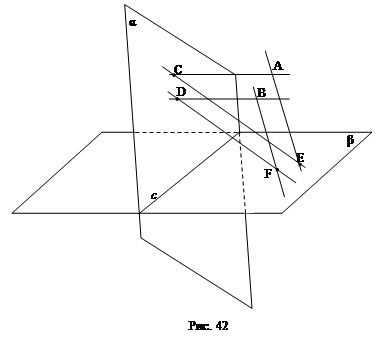
3.10. Прямая DF пересекает параллельные плоскости α, β и γ соответственно в точках D, Е и F, при этом DF = 3, ЕF = 9 (рис. 41). Прямая EG пересекает плоскости α и γ соответственно в точках G и Н, при этом EG = 12. Найдите длину GН.

Решение: Прямые EF и ЕH задают плоскость EFH, которая пересекает плоскости α и γ по прямым GD и FH соответственно. ∆GED

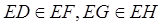
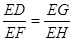
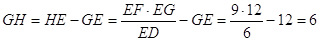
∆HEF (так как GD || FH, ). По свойству преобразования подобия: . Тогда .

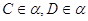
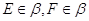
3.11. Плоскости α и β пересекаются по прямой с (рис. 42). Через точки А и В, расположенные вне этих плоскостей, проводятся параллельно плоскости β и параллельные между собой прямые АС и BD (), а также – параллельно плоскости α и параллельные между собой прямые АЕ и BF (). Докажите: а) плоскости АСЕ и BDF параллельны; б) плоскости АСЕ и BDF пересекают плоскости α и β по параллельным прямым.

Решение: а) GА || DB, АЕ || FВ по условию. По теореме о параллельности плоскостей (через пересекающиеся прямые): (АСЕ) || (DBF).

б) BF и АЕ задают плоскость, параллельную плоскости α. По свойству параллельных плоскостей: EF || с. Аналогично CD || c. По признаку параллельности прямых: CD || EF.

5.3. Уроки проверки знаний, умений и навыков

Для проверки знаний, умений и навыков разработаны три задачи на выявление типов оперирования пространственными образами: изменение пространственного положения образа (I тип); преобразование структуры образа (II тип); изменение положения и структуры образа одновременно (III тип).

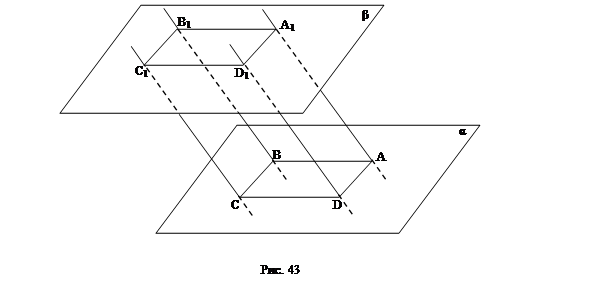
1. Через вершины параллелограмма ABCD, лежащего в одной из двух параллельных плоскостей, проведены параллельные прямые, пересекающие вторую плоскость в точках А₁, В₁, С₁ и D₁. Докажите, что четырехугольник А₁В₁С₁D₁ тоже параллелограмм (рис. 43).

Решение: АА₁ = DD₁ = СС₁ = ВВ₁ (отрезки параллельных прямых, заключенные между параллельными плоскостями, равны). Попарно параллельные прямые задают параллелограммы (задание плоскости через параллельные прямые), следовательно D₁А₁ || DА || СВ || С₁В₁. По определению А₁В₁С₁D₁ параллелограмм.

Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

1)
точки A,B,C и D не лежат в одной плоскости выберете верное утверждение.
1) прямая АB параллельна прямой CD.
2) прямая AB пересекает прямую CD.
3) Прямая АС пересекает прямую AD.
4) Прямые AB и CD 0 скрещиваются.

2)
Прямые a,b и с попарно пересекаются. Сколько плоскостей можно провести через эти прямые?
а)одну,б)две,б)три,г)ни одной. д)другой ответ.

3) прямая а параллельна прямой b, a прямая b пересекается с плоскостью а. Какие взаимное расположение прямой а и плоскости а?

4) Параллельные плоскости а и b, пересекают прямую MN в точках А и В, а прямую МР в точках С и D сответственно. Найдите MD, если АМ = 9см, АВ = 12 см и МС = 12 см.

5)
Постройте сечение тераэдра dmnk плоскостью, проходящей через точки А, В,: причем точка А принадлежит ребру nk, точка В принадлежит плоскости (ndk), а точка с -ебру МК.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Скрещивающиеся прямые. Проведение через одну из скрещивающихся прямых плоскости, параллельной другой прямой

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы рассмотрим определение скрещивающихся прямых и докажем теорему – признак скрещивающихся прямых. Далее рассмотрим три случая взаимного расположения двух прямых в пространстве. Докажем теорему о том, что через каждую из скрещивающихся прямых можно провести плоскость, параллельную другой прямой.
В конце урока решим несколько задач в тетраэдре на скрещиваемость прямых.