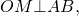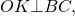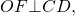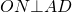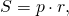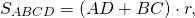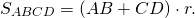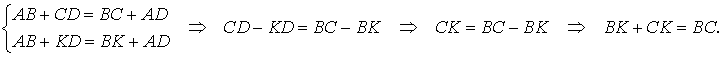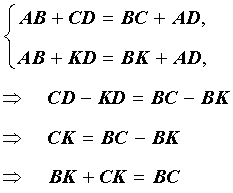Определение 1. Окружность называют вписанным в четырехугольник, если окружность касается всех сторон четырехугольника.
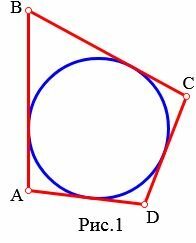
На рисунке 1 окружность вписан в четырехугольник ABCD. В этом случае говорят также, что четырехугольник описан около окружности.
 |
Теорема 1. Если окружность вписан в четырехугольник, то сумма противолежащих сторон четырехугольника равны.
Доказательство. Пусть окружность ABCD вписан в четырехугольник (Рис.2). Докажем, что ( small AB+CD=AD+BC ).
 |
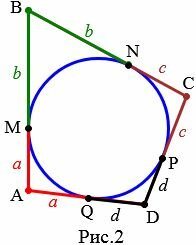Точки M, N, Q, P − точки касания окружности со сторонами четырехугольника. Так как отрезки касательных, проведенных к окружности через одну точку, равны (статья Касательная к окружности теорема 2), то
| ( small AM=AQ=a, ) ( small BM=BN=b, ) ( small CN=CP=c, ) ( small DQ=DP=d ) |
| ( small AB+CD ) ( small=AM+BM+CP+DP ) ( small =a+b+c+d, ) | (1) |
| ( small AD+BC) ( small=AQ+DQ+BN+CN) ( small=a+d+b+c. ) | (2) |
Из равенств (1) и (2), следует:
( small AB+CD=AD+BC. )  |
Теорема 2. Если в выпуклом четырехугольнике сумма противолежащих сторон равны, то в него можно вписать окружность.
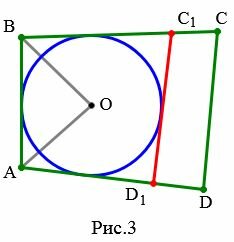
Доказательство. Пусть задан выпуклый четырехугольник ABCD и пусть ( small AB+CD=AD+BC. ) (Рис.3). Докажем, что в него можно вписать окружность.
 |
Проведем биссектрисы углов A и B четырехугольника ABCD. Точку их пересечения обозначим буквой O. Тогда точка O равноудалена от сторон AB, BC, AD. Следовательно существует окружность с центром в точке O, которая касается этих трех сторон.
Пусть эта окружность не касается стороны CD. Тогда возможны два случая.
Случай 1. Сторона CD не имеет общих точек с построенной окружностью.
Проведем касательную C1D1 к окружности, параллельно стороне CD четырехугольника.
Тогда окружность с центром O вписан в четырехугольник ABC1D1. Следовательно, по теореме 1, имеем:
| ( small AB+C_1D_1=AD_1+BC_1. ) | (3) |
Но по условию данной теоремы:
| ( small AB+CD=AD+BC. ) | (4) |
Вычтем из равенства (4) равенство (3):
| ( small CD-C_1D_1) (small=AD-AD_1+BC-BC_1 ) |
| ( small CD-C_1D_1=DD_1+CC_1 ) |
| ( small CD=DD_1+CC_1+C_1D_1) |
Получили, что в четырехугольнике CC1D1D длина одной стороны равна сумме длин трех остальных сторон, что невозможно (см. задачу 1 статьи Четырехугольник).
Таким образом сторона CD должна иметь общие точки с рассматриваемой окружностью.
Случай 2. Сторона CD имеет две общие точки с построенной окружностью (Рис.4).
 |
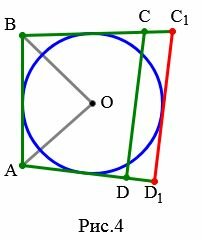Аналогичными рассуждениями можно показать, что сторона CD не может иметь две общие точки с построенной окружностью.
Следовательно, предполагая, что построенная окружность не касается стороны CD, мы пришли к противоречию. Таким образом, если в выпуклом четырехугольнике сумма противолежащих сторон равны, то в него можно вписать окружность.
Если в четырехугольник вписан окружность, то существует точка, равноудаленная от всех сторон четырехугольника. Эта точка является центром вписанной в четырехугольник окружности. Для нахождения этой точки достаточно найти точку пересечениия биссектрис двух соседних углов данного четырехугольника.
Вписанная в четырехугольник окружность
Описанный четырехугольник — это четырехугольник, все стороны которого касаются окружности. При этом окружность называется вписанной в четырехугольник.
Какими свойствами обладает вписанная в четырехугольник окружность? Когда в четырехугольник можно вписать окружность? Где находится центр вписанной окружности?
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противолежащих сторон равны.
В четырехугольник ABCD можно вписать окружность, если
И обратно, если суммы противоположных сторон четырехугольника равны:
то в четырехугольник ABCD можно вписать окружность.
Центр вписанной в четырехугольник окружности — точка пересечения его биссектрис.
O — точка пересечения биссектрис четырехугольника ABCD.
AO, BO, CO, DO — биссектрисы углов четырехугольника ABCD,
то есть ∠BAO=∠DAO, ∠ABO=∠CBO и т.д.
3. Точки касания вписанной окружности, лежащие на сторонах, выходящих из одной вершины, равноудалены от этой вершины.
AM=AN,
5. Площадь четырехугольника связана с радиусом вписанной в него окружности формулой
где p — полупериметр четырехугольника.
Так как суммы противолежащих сторон описанного четырехугольника равны, полупериметр равен любой из пар сумм противолежащих сторон.
Например, для четырехугольника ABCD p=AD+BC или p=AB+CD и
Соответственно, радиус вписанной в четырехугольник окружности равен
Описанные четырехугольники
Определение 1 . Окружностью, вписанной в четырёхугольник, называют окружность, которая касается касается каждой из сторон четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, описанным около окружности или описанным четырёхугольником .
Замечание . В настоящем разделе мы рассматриваем только выпуклые четырёхугольники.
Теорема 1 . Если четырёхугольник описан около окружности, то суммы длин его противоположных сторон равны.
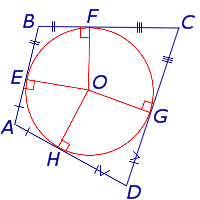
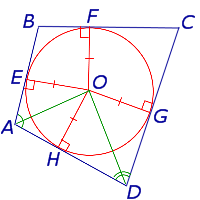
Доказательство . Рассмотрим четырёхугольник ABCD , описанный около окружности, и обозначим буквами E, F, G, H – точки касания сторон четырёхугольника с окружностью (рис.2).
AH = AE, BF = BE, CF = CG, DH = DG,
Складывая эти равенства, получим:
AH + BF + CF + DH =
= AD + BC,
AE + BE + CG + DG =
= AB + CD,
то справедливо равенство
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1) . Если у четырёхугольника суммы длин противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.
Доказательство . Рассмотрим четырёхугольник ABCD , длины сторон которого удовлетворяют равенству
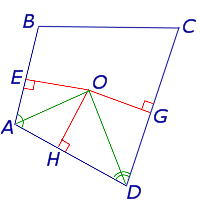
и проведём биссектрисы углов BAD и CDA . Обозначим точку пересечения этих биссектрис буквой O , и опустим из точки O перпендикуляры OH, OE и OG на стороны AD, AB и CD соответственно (рис.3).
Следовательно, справедливы равенства
из которых вытекает, что точки H, E и G лежат на окружности с центром в точке O и радиусом OH , касающейся сторон четырёхугольника AD, AB и CD в точках H, E и G соответственно. При этом возможны два случая:
Окружность касается касается стороны BC (рис.4).
В этом случае четырёхугольник ABCD описан около окружности, и теорема доказана.
Окружность не касается стороны BC .
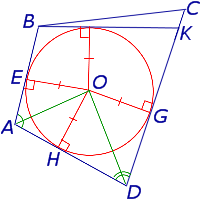
В этом случае касательная, проведенная к окружности из точки B , пересекает прямую DC в точке K , и возможны два случая:
- Точка K лежит между точками C и D (рис.5)
Рассмотрим случай 2а и приведём его к противоречию. В этом случае в силу того, что четырёхугольник ABKD является описанным, а также по условию теоремы справедливы равенства:
Последнее равенство утверждает, что в треугольнике BKC сумма двух сторон равна третьей стороне, что противоречит неравенству треугольника неравенству треугольника неравенству треугольника . Полученное противоречие доказывает, что случай 2а невозможен.
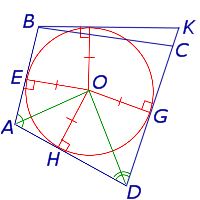
Совершенно аналогичные рассуждения позволяют заключить, что случай 2b также невозможен.
Итак, возможен и реализуется лишь случай 1.
Из доказательства теоремы 2 непосредственно вытекает
Теорема 3 . Биссектрисы всех внутренних углов описанного четырёхугольника пересекаются в одной точке – центре вписанной окружности.
В следующей таблице приводятся примеры четырёхугольников, в которые можно вписать окружность. Доказательства утверждений непосредственно вытекают из теорем 1 и 2 и предоставляются читателю в качестве несложных упражнений.
Примеры описанных четырёхугольников
| Фигура | Рисунок | Утверждение |
| Ромб | 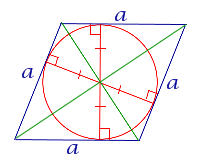 | В любой ромб можно вписать окружность |
| Квадрат | 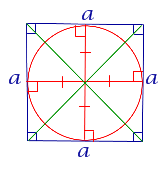 | В любой квадрат можно вписать окружность |
| Прямоугольник | 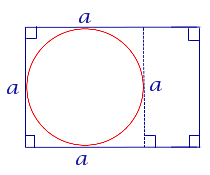 | В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом |
| Параллелограмм | 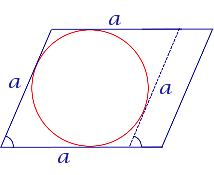 | В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом |
| Дельтоид | 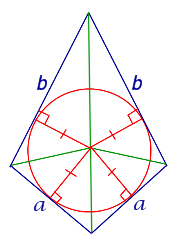 | В любой дельтоид можно вписать окружность |
| Трапеция | 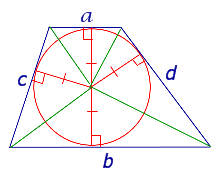 | В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон рана сумме длин оснований |
| Ромб |
|
В любой квадрат можно вписать окружность
В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом
В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом
В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон рана сумме длин оснований