Средняя оценка: 4.5
Всего получено оценок: 250.
Средняя оценка: 4.5
Всего получено оценок: 250.
В школьном курсе геометрии изучают разные виды треугольников. В задачах очень часто рассматривают остроугольный треугольник, поэтому стоит особенно пристально изучить свойства этой фигуры.
- Определение понятия
- Характеристики
- Линии остроугольного треугольника
- Свойства
- Что мы узнали?
- Остроугольный треугольник — виды, свойства и признаки
- Виды, признаки и свойства остроугольных треугольников
- Равносторонний треугольник
- Разносторонний треугольник
- Равнобедренный остроугольный треугольник
- Равнобедренный тупоугольный треугольник
- Треугольник. Формулы определения и свойства треугольников.
- Определение треугольника
- Классификация треугольников
- 1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
- 2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
- 3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
- 4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
- 5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
- 6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
- Свойства треугольника
- 1.Свойства углов и сторон треугольника.
- 2.Теорема синусов.
- 3. Теорема косинусов.
- 4. Теорема о проекциях
- Медианы треугольника
- Свойства медиан треугольника:
- Формулы медиан треугольника
- 📹 Видео
Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Определение понятия
Треугольником называют фигуру, состоящую из трех точек, и трех отрезков их соединяющих. В зависимости от углов треугольник может быть:
- Прямоугольным, если один из углов равен 90 градусов;
- Тупоугольный, если один из углов тупой, т.е. больше 90 градусов;
- Остроугольным, если все углы треугольника острые.
Для решения задач с остроугольными треугольниками часто приходится использовать теорему синусов или косинусов.
Еще в Древней Греции математики изучали треугольники. Именно греки разработали основы современной геометрии, куда входит и множество теорем о треугольниках. Например, автор теоремы Пифагора родом из Древней Греции.
Видео:Всё про прямоугольный треугольник за 15 минут | Осторожно, спойлер! | Борис Трушин !Скачать

Характеристики
В остроугольном треугольнике каждый угол меньше 90 градусов. Но сумма углов в треугольнике всегда равна 180. В любой фигуре вершины обозначают заглавными латинскими буквами.
Одним из элементов треугольника, вместе со сторонами и углами, является внешний угол. Внешний угол это угол, смежный с внутренним углом треугольника.
У любого треугольника 6 внешних углов, по 2 на каждый внутренний. Любой внешний угол остроугольного треугольника всегда будет тупым.
Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Линии остроугольного треугольника
Остроугольный треугольник обладает рядом свойств.
Медиана геометрической фигуры будет делить сторону, на которую она опущена, пополам. Причем можно провести этот отрезок с любой вершины. Медианы пересекаются в одной точке, и эта точка делит каждую из них в отношении 2:1.
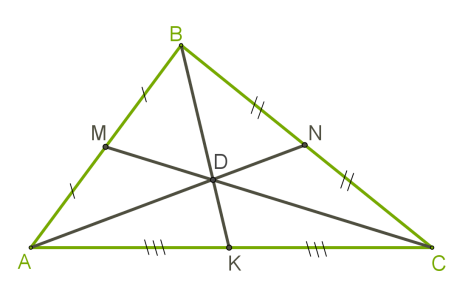
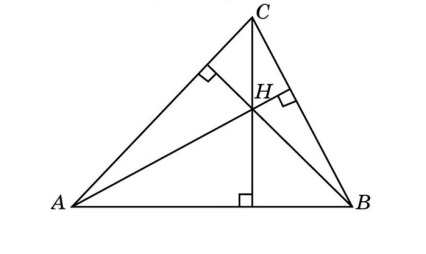
Известно, что если провести три высоты в остроугольном треугольнике, то они будут пересекаться в одной точке, которую называют ортоцентром. Эти отрезки опускают под прямым углом к противоположным сторонам. Высоты в остроугольном треугольнике разделяют эту фигуру на прямоугольные треугольники.
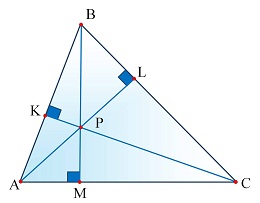
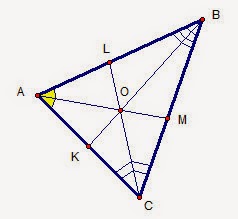
Биссектрисы в остроугольном треугольнике не только делят углы пополам. Эти отрезки пересекаются в точке, которая является центром вписанной окружности.
Также биссектриса разделяет сторону остроугольного треугольника на две части, которые пропорциональны соответствующим боковым сторонам. Данное утверждение нужно запомнить, чтобы решать некоторые задачи.
Видео:7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Свойства
Если суммировать числовые значения любых двух сторон остроугольного треугольника, то обязательно получим цифру, которая будет больше третьего отрезка данной геометрической фигуры.
Средняя линия в остроугольном треугольнике параллельна одной из сторон данной фигуры и равна ее половине.
Видео:№16 из ЕГЭ2022 и олимпиады. Красивое доказательство свойства ортоцентра остроугольного треугольникаСкачать

Что мы узнали?
В остроугольном треугольнике каждый угол меньше 90 градусов. Общая сумма углов здесь также равняется 180 градусов. Нельзя забывать о характерных линиях треугольника. Поскольку с их помощью легко вычислить стороны данной треугольной фигуры или центр определенной окружности. А если в условиях задач по геометрии указаны углы, то можно воспользоваться тригонометрическими функциями.
Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Остроугольный треугольник — виды, свойства и признаки
Одна из центральных тем на уроках геометрии – остроугольный треугольник, составная часть своих более сложных аналогов и иных тригонометрических форм.
Азы изучения точной науки начинаются с рассмотрения уникальной комбинации из трех сторон и острых углов.
Видео:Математика | Метрические соотношения в прямоугольном треугольникеСкачать

Виды, признаки и свойства остроугольных треугольников
Трехсторонние фигуры разделяются на множество подвидов и категорий.
Общая классификация по наибольшему углу делит их на 3 группы:
Они располагают как общими для формы с тремя сторонами характеристиками, так и специфическими признаками.
3 угла, сумма которых равна 180°, (величина каждого меньше 90°) и 3 стороны;
сумма длин любых двух сторон больше оставшейся третьей.
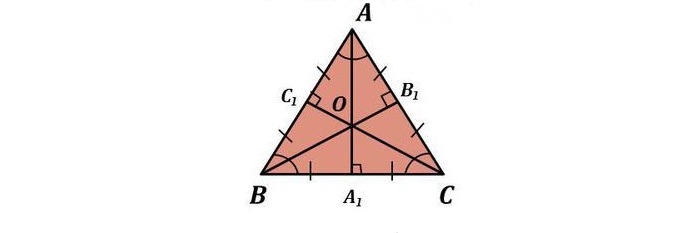
Свойства остроугольной фигуры определяются вспомогательными геометрическими линиями, всегда находящимися внутри него:
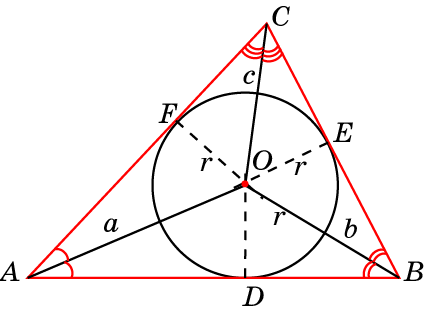
1. Биссектрисы, делящие углы пополам, являются центром, вокруг которого можно нарисовать вписанную окружность.
2. Высоты пересекаются в одной точке, образуя ортоцентр.
3. Медианы в точке пересечения пролегают в пропорции 2:1 (2 трети до центра и 1 треть после).
Уникальные особенности зависят от разновидностей фигуры.
Видео:В остроугольном треугольнике все углы острые. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Равносторонний треугольник
«Идеальный» правильный треугольник, облегчающий решение задач. Определение, форма и свойства данной геометрической формы исходят из названия — все углы равны 60°, а стороны равны друг другу.
Полное равенство придает и другую особенность: медианы, биссектрисы и высоты полностью совпадают.
Видео:Построение медианы в треугольникеСкачать

Разносторонний треугольник
Наиболее часто встречаемый на чертежах в геометрии вариант, один из самых трудноразрешимых видов. Разносторонними бывают и прямоугольные, и тупоугольные фигуры.
Уникальных отличий не имеет, только общие:
все параметры имеют разные значения;
совпадений между вспомогательными линиями нет.
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Равнобедренный остроугольный треугольник
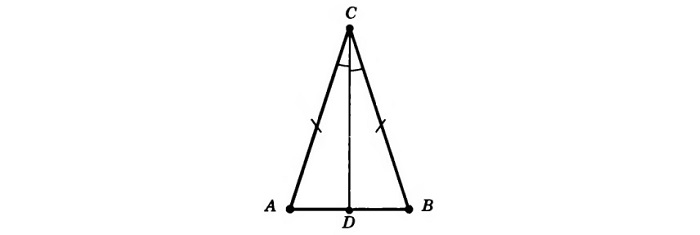
Здесь при основании (стороне, не равной остальным) находятся равные друг другу 2 стороны и 2 угла. Выглядит как вытянутый в одну сторону равносторонний треугольник.
проведенная к основанию линия – и биссектриса, и высота, и медиана;
вспомогательные линии из крайних точек при основании совпадают.
Видео:Треугольники: остро-, тупо- и прямоугольныеСкачать

Равнобедренный тупоугольный треугольник
Пусть он и называется равнобедренным, но из-за наличия угла более 90° не является остроугольным и является представителем другой группы.
Начертить его сложнее (рисунок следует начинать с основания и 2 острых углов и уже после создавать тупой), но процесс решения и изучения прост.
Отличие у него одно – точка пересечения двух высот, проведенных от углов при основании, выходит за периметр треугольника. Чтобы ее обозначить, необходимо нарисовать «продолжения» равнобедренных линий. Все остальные свойства совпадают.
В ключевых и фундаментальных разделах математики именно треугольник является основой для доказательства многих теорем и помощью в решении множества задач. Твердое знание его свойств откроет путь к успехам в расчетах, вычислениях, оформлении чертежей и фото в проектных работах.
Видео:Виды треугольниковСкачать

Треугольник. Формулы определения и свойства треугольников.
В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры — треугольника. А также разберем некоторе примеры решения задач на треугольники.
Содержание:
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Определение треугольника
Треугольник — это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом — △, после которго пишут названия вершин треугольника напр. △ABC.
Треугольник ABC (△ABC)
- Точки A, B и C — вершины треугольника. Принято писать их большими буквами.
- Отрезки AB, BC и СА — стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
- Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b — β, с — γ.
Углы треугольника, также, можно обозначать специальным символом — ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:
Видео:Высота в прямоугольном треугольнике. 8 класс.Скачать

Классификация треугольников
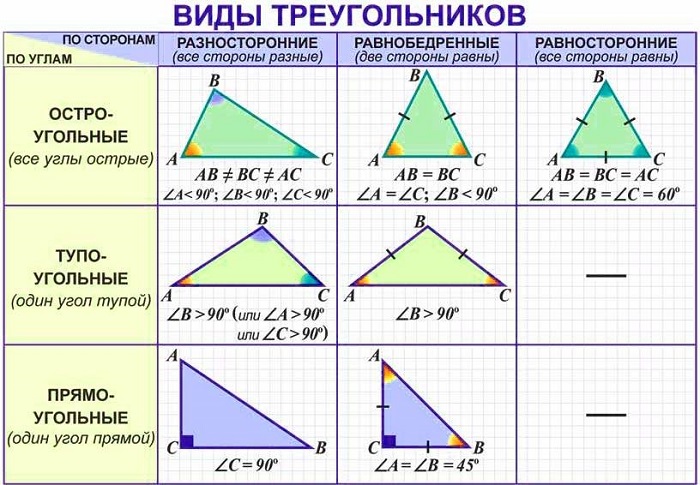
Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.
1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
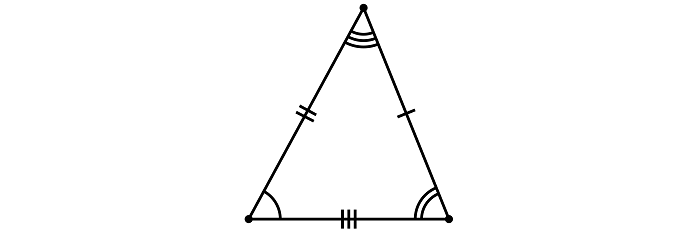
2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
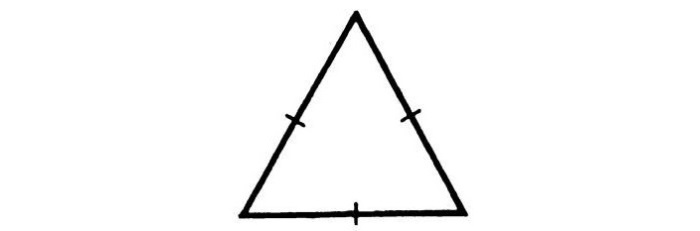
3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
Видео:Построение высоты в треугольникеСкачать

Свойства треугольника
1.Свойства углов и сторон треугольника.
- Сумма всех углов треугольника равна 180°:
- Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
- В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
2.Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c |
| sin α | sin β | sin γ |
3. Теорема косинусов.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
4. Теорема о проекциях
Для остроугольного треугольника:
Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

Медианы треугольника
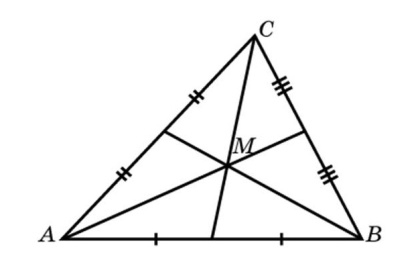
Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)
2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
| AO | = | BO | = | CO | = | 2 |
| OD | OE | OF | 1 |
3. Медиана треугольника делит треугольник на две равновеликие по площади части
4. Треугольник делится тремя медианами на шесть равновеликих треугольников.
5. Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны:
📹 Видео
Остроугольный треугольникСкачать
В тупоугольном треугольнике все углы тупые. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Построение биссектрисы в треугольникеСкачать