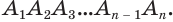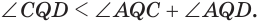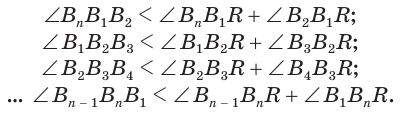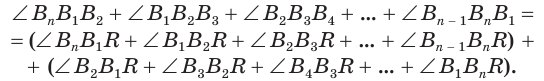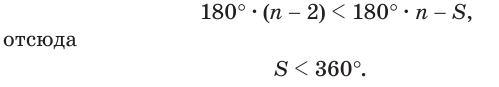Содержание

Геометрия, 11 класс. Задачник (Е. В. Потоскуев, Л. И. Звавич) 2004
Страница № 031.
OCR-версия страницы из учебника (текст страницы, которая находится выше):
Нетрадиционная форма урока. Зачет по теме в 11-м классе «Многогранники»
Правильные многогранники в геометрии с примерами
🎦 Видео

Геометрия, 11 класс. Задачник (Е. В. Потоскуев, Л. И. Звавич) 2004

Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

Страница № 031.

Учебник: Геометрия. 11 кл.: Задачник для общеобразовательных учреждений с углуб. и профильным изучением математики / Е. В. Потоскуев, Л. И. Звавич. — 2-е изд., стереотип. — М.: Дрофа, 2004. — 240 с.: ил.

Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

OCR-версия страницы из учебника (текст страницы, которая находится выше):

^ МНОГОГРАННИКИ

Задачи к § 9. Понятие многогранника

2.001. © Является ли телом фигура: а) состоящая из двух шаров, не имеющих общих точек; б) состоящая из двух шаров, имеющих одну общую точку; в) являющаяся объединением двух кубов, имеющих общую вершину (общее ребро)? Ответ поясните на рисунке.

2.002. © Тело F является пересечением двух тел F₁ и F₂. Каким будет тело F, если F₁viF₂ — выпуклые тела?

2.003. Приведите пример тела, каждое сечение которого плоскостью, проходящей через некоторую прямую, состоит из двух равных кругов.

2.004. © Начертите многогранник, у которого сечениями могут быть: а) квадрат; прямоугольник; правильный треугольник; правильный шестиугольник; трапеция; ромб; б) правильный треугольник; квадрат; трапеция.

2.005. Назовите многогранник, имеющий наименьшее число граней. Сколько у него вершин, ребер?

2.006. © Может ли гранью пятигранника быть: а) четырехугольник; б) пятиугольник? Ответ поясните на рисунке.

2.007. Одна из граней многогранника — пятиугольник, а) Какое наименьшее число ребер может иметь этот многогранник? б) Какое наименьшее число граней может иметь этот многогранник?

2.008. Начертите многогранник, имеющий: а) шесть ребер;

б) восемь ребер; в) девять ребер.

2.009. © Начертите несколько различных разверток: а) правильного тетраэдра; б) куба.

2.010. © В кубе ABCDA₁B₁C₁D₁ проведено сечение через середины ребер А₁Б₁, В₁С₁ и точку D, разбившее куб на два многогранника. Определите количество ребер, вершин и граней того из них, которому принадлежит вершина В.

Видео:ЗАДАЧА ПРО ПЯТИУГОЛЬНИКСкачать

Нетрадиционная форма урока. Зачет по теме в 11-м классе «Многогранники»

Разделы: Математика

Существует несколько разновидностей нетрадиционных форм урока, каждая из которых решает свои образовательные, развивающие, воспитательные задачи. Однако все они преследуют и общую цель: поднять интерес учащихся к учёбе и математике, тем самым повысить эффективность обучения. Для учащихся нетрадиционный урок – это возможность развивать свои творческие способности и личностные качества, оценить роль знаний и применить их на практике, это самостоятельность и совсем другое отношение к труду. Одной из форм организации контроля знаний, умений и навыков учащихся является урок – зачёт. Основная его цель состоит в диагностике уровня усвоения знаний и умений каждым учащимся на определённом этапе обучения. За 10-15 дней вывешиваю примерный перечень теоретических и практических вопросов, выносимых на зачёт. К проведению зачётного занятия привлекаю учащихся, наиболее успешно осваивающих математику.

Их специально к этому готовлю, проверяю их знания, объясняю их обязанности на таком занятии. Вместе с ними распределяю учащихся по группам (в каждой группе 3 человека), групповоды (консультанты) готовят листки учёта знаний, в которых будут фиксироваться отметки за выполнение каждого задания и итоговые отметки за зачёт.

Зачёт принимается по картам, включающим основные теоретические вопросы и типовые задачи темы, и дополнительные вопросы. Эффективность урока-зачёта во многом зависит от содержания заданий карт, поэтому при подготовке карт для зачёта очень серьёзно подхожу к отбору материала. Итоговая отметка ставится в листке учёта знаний на основе результатов за все задания с учётом мнения групповода.

Привожу примеры карт для проведения зачёта в 11 классе по теме «Многогранники», геометрия в этом классе изучается по учебнику Погорелова А.В. «Геометрия 7-11».

I ВАРИАНТ

I. Устные упражнения.

В основании пирамиды лежит прямоугольник АВСД, а одно из боковых ребер РВ перпендикулярно основанию. Постройте линейный угол двугранного угла при ребре АВ.
Запишите план построения правильной треугольной пирамиды. Построите эту пирамиду.
Можно ли составить трехгранный угол из плоских углов:
а) 120°; 60°; 90°;
б) 150°; 120°; 90°. Объясните свой ответ.
Сколько трехгранных углов имеет тетраэдр?
Может ли гранью пятигранника служить: а) четырехугольник; в) пятиугольник?
Существует ли призма, у которой только одно боковое ребро перпендикулярно к плоскости основания? Ответ объясните.
Если в пирамиде все боковые ребра равны, то вершина ее проектируется в центр описанной около основания окружности. Докажите.
Является ли перпендикулярность бокового ребра призмы к плоскости основания необходимым условием того, что призма правильная?
Верно ли утверждение, что прямоугольный параллелепипед есть правильная призма?
Можно ли считать линейным углом двугранного угла угол, стороны которого — два луча, проведенные в гранях двугранного угла из одной точки ребра?

II. Докажите, что у параллелепипеда противолежащие грани параллельны и равны.

III. Решите задачи:

а) Найдите площадь поверхности прямоугольного параллелепипеда у которого диагональ равна 13 дм, высота 12 дм, а одно из ребер основания 4 дм.

в) В правильной треугольной пирамиде боковые ребра наклонены к плоскости основания под углом 30° .Сторона основания равна 12 см. Найдите высоту пирамиды.

II ВАРИАНТ

I. Устные упражнения.

В основании пирамиды лежит прямоугольник АВСД, а одно из боковых ребер РВ перпендикулярно основанию. Построите линейный угол двугранного угла при ребре ВС.
Запишите план построения правильной четырехугольной пирамиды. Постройте эту пирамиду.
Можно ли составить трехгранный угол из плоских углов:
а) 150°; 140°: 120°;
б) 150°; 90°; 60°. Объясните свой ответ.
Равен ли линейному углу двугранного угла угол между двумя лучами, перпендикулярными его ребру и лежащими в его гранях?
Сколько трехгранных углов имеет параллелепипед?
Назовите многогранник, имеющий наименьшее число граней. Сколько у него ребер, вершин, диагоналей?
Одна из граней многогранника — шестиугольник. Какое наименьшее число ребер может иметь этот многогранник?
Если в пирамиде все двугранные углы при основании равны, то вершина ее проектируется в центр вписанной в основание окружности. Докажите.
Верно ли утверждение, что все грани прямоугольного параллелепипеда – прямоугольники?
Является ли перпендикулярность бокового ребра призмы к плоскости основания достаточным признаком того, что призма правильная

II. Докажите, что диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.

III. Решите задачи:

а) В правильной треугольной призме длина бокового ребра равна 18 см., а сторона основания 24 см. Наедите периметр сечения, проведенного через сторону нижнего основания и противоположную вершину верхнего основания.

в) В правильной четырехугольной пирамиде сторона основания 10 м, высота 12 м. Найдите площадь поверхности пирамиды.

III ВАРИАНТ

I. Устные упражнения.

В основании пирамиды лежит прямоугольник АВСД, а одно из боковых ребер РВ перпендикулярно основанию. Построите линейный угол двугранного угла при ребре СД.
Запишите план построения правильной шестиугольной пирамиды. Построите эту пирамиду.
Можно ли составить трехгранный угол из плоских углов:
а) 100°; 120°; 10°;
б) 125°; 120°; 115°. Объясни те свой ответ.
Какое минимальное число граней может иметь призма? Сколько вершин, ребер, боковых ребер у такой призмы?
В кубе АВСДА₁ B₁ С₁ Д₁ проведено сечение через вершину А С Д.
Каков вид пирамиды Д₁ A₁ C₁ Д?
Будет ли кубом параллелепипед, если известно, что при двух вершинах одного и того же ребра равны все ребра и плоские углы? Ответ объясните.
В пирамиде SABC все боковые ребра равны, а основание — прямоугольный треугольник. Постройте пирамиду, проведите в ней высоту и опишите построение и его обоснование.
Сколько боковых ребер пирамиды могут быть перпендикулярны к плоскости основания?
Верно ли утверждение, что все грани прямого параллелепипеда — прямоугольники? Существует ли параллелепипед, у которого только одна боковая грань перпендикулярна основанию?

II. Докажите теорему о свойстве диагонали прямоугольного параллелепипеда.

III. Решите задачи:

а) В прямой прямоугольной призме основание — прямоугольный треугольник с катетом 8 см и 6 см. Боковое ребро приемы равно 12 см. Найдете площадь полной поверхности призмы.

в) В правильной треугольной пирамиде через середины трех боковых ребер проведено сечение. Найдите его площадь, если длина ребра основания пирамиды равна 24 см.

Видео:Измерение угла с помощью транспортираСкачать

Правильные многогранники в геометрии с примерами

Пусть есть плоский многоугольник

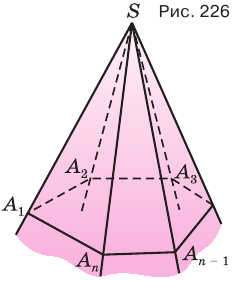
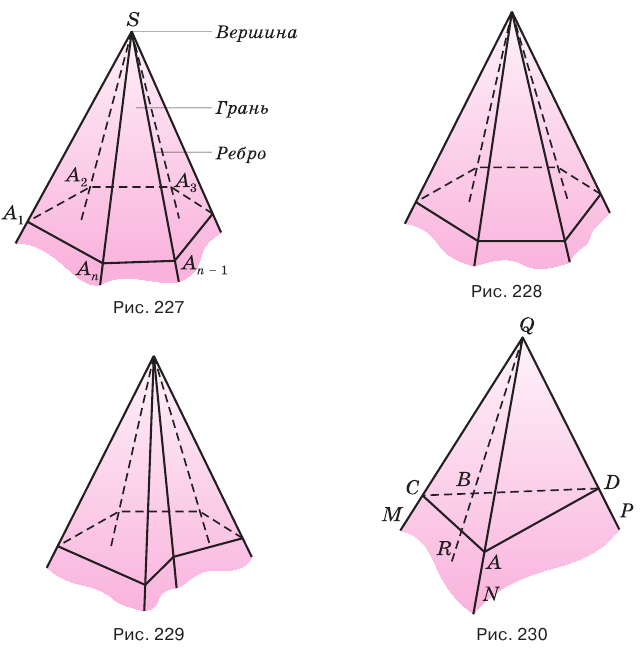
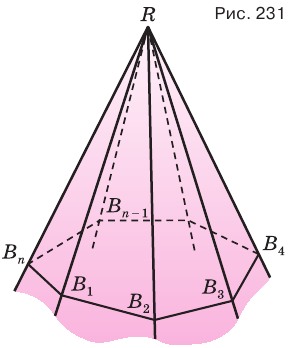
Многогранный угол называется выпуклым, если он расположен по одну сторону от плоскости любой его грани. Многогранный угол на рисунке 228 выпуклый, а на рисунке 229 — невыпуклый. По количеству граней многогранные углы разделяют на трехгранные, четырехгранные и т. д.

Теорема 12.

Сумма плоских углов выпуклого многогранного угла меньше 360°.

Доказательство:

Установим сначала, что каждый плоский угол трехгранного угла меньше суммы двух других его углов.

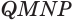
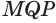
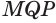
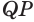
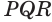
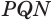
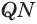
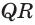
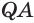
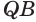
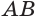
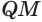
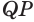
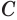
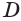
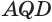
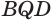
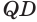
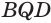
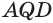
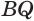
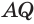
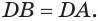
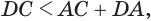
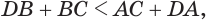
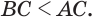
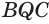
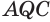
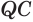
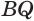
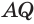
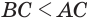
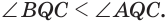
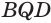
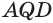
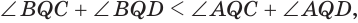
Пусть есть трехгранный угол (рис. 230). Пусть для определенности угол — больший из плоских углов трехгранного угла. В плоскости грани от луча отложим угол , равный углу , и на лучах и отложим равные отрезки и . Через прямую проведем такую плоскость, которая пересекает ребра и в некоторых точках и . Треугольники и равны, так как у них сторона общая, и по построению равны углы и , а также стороны и . Значит, Далее по свойству сторон треугольника получаем или или Теперь, поскольку у треугольников и сторона общая, стороны и равны, но , то Прибавив к левой и правой частям этого неравенства соответственно углы и , которые равны друг другу, получим, что или

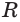
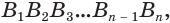
Пусть теперь есть выпуклый многогранный угол с вершиной (рис. 231). Если пересечь его какой-либо плоскостью, то в сечении получим многоугольник каждая вершина которого является вершиной трехгранного угла, образованного двумя гранями данного угла и секущей плоскостью. По доказанному для этих трехгранных углов получаем:

Сложим покомпонентно эти неравенства:

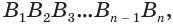
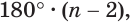
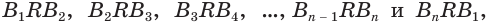
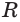
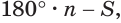
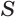
Теперь обратим внимание на то, что сумма в левой части последнего неравенства есть сумма углов многоугольника которая равна а в правой — сумма углов всех треугольников но без их углов при вершине , которая равна где выражает сумму плоских углов данного многогранного угла. Таким образом,

Многогранник, у которого все грани являются равными правильными многоугольниками и все двугранные углы равны друг другу, называется правильным многогранником.

Из этого определения следует, что у правильного многогранника равны друг другу все его:

Теорема 13.

Количество ребер, сходящихся в каждой вершине правильного многогранника, не больше пяти.

Доказательство:

Допустим, что это не так, т. е. в вершине многогранника сходится шесть или больше ребер. Тогда при этой вершине многогранник имел бы шесть или больше равных плоских углов. Учитывая, что сумма этих углов меньше 360°, получаем, что каждый из них меньше 60°. Но это невозможно, поскольку гранями правильного многогранника являются правильные многоугольники, а у них углы не меньше 60°.

Теорема 14.

Количество сторон правильного многоугольника, являющегося гранью правильного многогранника, не больше пяти.

Доказательство:

В каждой вершине правильного многогранника сходится не менее трех плоских углов, а поэтому каждый из них должен быть меньше 120°. Вместе с этим угол правильного шестиугольника равен 120°, а угол правильного многоугольника с большим количеством сторон больше 120°. Поэтому правильные многоугольники, количество сторон которых больше пяти, не могут быть гранями правильного многоугольника.

Теорема 15.

Есть пять типов правильных многогранников.

Доказательство:

В соответствии с теоремой 14 гранями многогранника могут быть правильные треугольники, четырехугольники или пятиугольники.

Если гранями правильного многогранника служат треугольники, то, с учетом теоремы 13, в вершинах многогранника могут сходиться три, четыре или пять ребер. Если гранями правильного многогранника служат четырехугольники или пятиугольники, то в вершинах многогранника может сходиться только три ребра. Значит, существует не более пяти видов правильных многогранников.

Чтобы убедиться, что такие виды многогранников существуют, достаточно указать способ построения каждого из них.

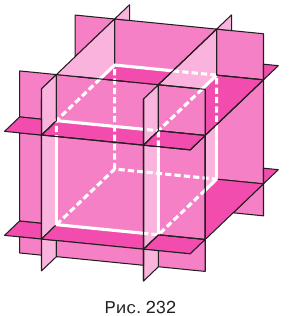
Прежде всего отметим, что правильным многогранником, гранями которого служат правильные четырехугольники, т. е. квадраты, является куб, который еще называют правильным гексаэдром. Куб можно построить так. В произвольно выбранной плоскости построить квадрат, через его стороны провести плоскости, перпендикулярные выбранной плоскости, и провести еще одну плоскость, параллельную выбранной плоскости и отстоящую от нее на сторону квадрата (рис. 232). Мы видим, что гексаэдр имеет 6 граней, 12 ребер и 8 вершин.

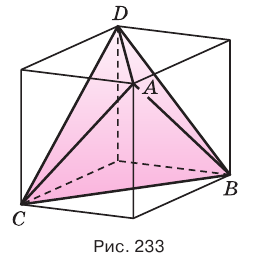
Построение многогранника, в каждой вершине которого сходится по три треугольные грани, может быть таким. Построить куб. Выбрать одну из его вершин и в каждой грани с этой вершиной выбрать вершину, противолежащую вершине . Пусть это вершины , , . Точки , , , являются вершинами искомого многогранника (рис. 233). Действительно, каждый из отрезков является диагональю одной из граней куба, а поэтому все эти отрезки равны друг другу. Получается, что в треугольной пирамиде все грани являются правильными треугольниками. Такая пирамида называется правильным тетраэдром. Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.

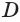
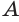
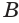
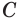
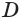
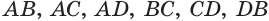
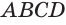
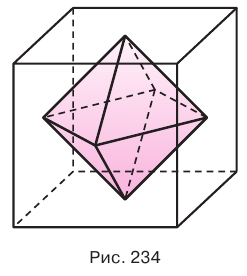
Построение многогранника, в каждой вершине которого сходится по четыре треугольные грани, может быть таким. Построить куб и найти центры шести его граней (рис. 234). Эти точки являются вершинами многогранника, все грани которого — правильные треугольники. Такой многогранник называется правильным октаэдром. Октаэдр имеет 8 граней, 12 ребер и 6 вершин.

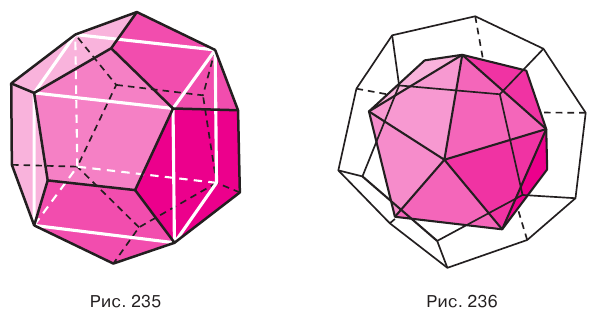
Построение многогранника, в каждой вершине которого сходится по три пятиугольные грани, можно выполнить, снова используя куб. Если через каждое из двенадцати ребер куба провести плоскость, которая не имеет с поверхностью куба других общих точек, кроме точек этого ребра, то полученные 12 плоскостей при пересечении дадут грани некоторого многогранника. Можно так подобрать наклон этих плоскостей к граням куба, что грани этого двенадцатигранника будут правильными пятиугольниками (рис. 235). Такой многогранник называется правильным додекаэдром. Додекаэдр имеет 12 граней, 30 ребер и 20 вершин.

Наконец, многогранник, в каждой вершине которого сходится по пять треугольных граней, можно построить, используя додекаэдр: центры граней додекаэдра являются вершинами искомого правильного многогранника (рис. 236). Такой многогранник называется правильным икосаэдром. Икосаэдр имеет 20 граней, 30 ребер и 12 вершин.

Таким образом, есть пять типов правильных многогранников.

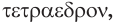
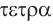
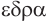
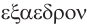
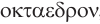
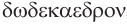
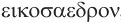
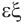
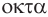
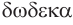
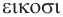
Названия правильных многогранников происходят из греческого языка. Термин тетраэдр, по-гречески означает четырехгранник: — четыре и — грань. Соответственно термины гексаэдр, октаэдр, додекаэдр, икосаэдр, по-гречески , , , , означают шестигранник, восьмигранник, двенадцатигранник, двадцатигранник: , — шесть, — восемь, — двенадцать, — двадцать.

Мы знаем, что правильные гексаэдр и тетраэдр имеют описанный и вписанный шары. Также описанный и вписанный шары имеют октаэдр, додекаэдр и икосаэдр. Центры этих шаров совпадают, и эта точка является центром симметрии соответствующего правильного многогранника, кроме тетраэдра, который не имеет центра симметрии.

Рекомендую подробно изучить предметы:

Геометрия
Аналитическая геометрия
Начертательная геометрия

Ещё лекции с примерами решения и объяснением:

Многогранники
Окружность
Эллипс
Гипербола
Пирамида в геометрии
Конус в геометрии
Сфера в геометрии
Шар в геометрии

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.