Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Интернет-олимпиада компании IBM
- IV Интернет-олимпиада по математике/XIV тур Математического Марафона (12)→
- XV тур математического марафона (12)→
- Вторая открытая Интернет-олимпиада по математике (9)→
- Третья Интернет-олимпиада по математике/XIII тур Математического Марафона (12)→
- Задачи конкурса Ponder This компании IBM: 7↓
- Задача о плитках домино
- Решение числового ребуса
- Ферзи на шахматной доске
- Задача о четырёх точках
- Лягушка на числовой прямой
- Разрезание квадратной доски
- Как выиграть в лотерею
- Задачи областной олимпиады по математике 2010 (5)→
- Первая открытая Интернет-олимпиада по математике (9)→
- Задачи областной олимпиады по математике 2009 (5)→
- Как доказывать олимпиадные неравенства
- Задачи международного турнира
- XXI тур Математического Марафона
- Отбор на XVI Всеукраинский турнир — Часть 2
- Отбор на XVI Всеукраинский турнир — Часть 1
- Далеко, далеко, на лугу пасутся ко.
- Людоед и гномики
- Поиск фальшивой монеты
- Два парома
- Как вычислять бесконечные суммы: часть 1
- Вариации на тему игры Баше
- Мотоциклист, велосипедист и пешеход
- Утроение числа после перестановки цифр
- Как вычислять бесконечные суммы: часть 2
- Задача о поиске радиоактивных шаров
- Нестандартное решение задачи по теории вероятности
- Математические маневры
- Задача о двух мудрецах
- Ранжирование грузов по весу
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Задача
На плоскости даны четыре точки. Известно, что шесть попарных расстояний между ними принимают только два различных значения. Какие конфигурации могут образовывать эти точки и каким будет отношение между двумя различными расстояниями?
Впервые я узнал про эту задачу на ежемесячном конкурсе IBM Ponder This, решил её и вскоре с гордостью обнаружил своё имя в списке победителей. А через некоторое время увидел её в сборнике всесоюзных олимпиад где-то за 1936 год. Собственно, задача хороша тем, что проста для понимания и достаточно нетривиальна для разбора. Ниже привожу собственный вариант решения, который я отправлял в IBM. Если вы не торопитесь глядеть в ответ (похвально!), но хотите проверить, все ли вы конфигурации нашли, могу сообщить, что их должно быть 6 (или 9, если ещё кое о чём вспомнить)
Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Решение
Рассмотрим 3 различных случая:
- 5 расстояний равны a и шестое расстояние равно b. Тогда обязательно найдётся равносторонний треугольник со сторонами, равными a. Расстояния от четвёртой точки до двух вершин треугольника должно также равняться a, и вместе с отрезком, соединяющим эти две вершины, получится ещё один равносторонний треугольник. Точка D должна лежать в другой полуплоскости относительно BC, чем точка A. Мы получаем ромб со сторонами и одной диагональю a, тогда длина шестого отрезка b=
 (рис.1)
(рис.1)Рис.2. Находим точки пересечения
Рис.3. Верхняя точка пересечения
Рис.4.Нижняя точка пересечения
Рис.6.Центр описанной окружности
Поскольку расстояние, равное нулю – тоже расстояние, то добавляется ещё 3 варианта расположения точек согласно условию задачи:.
- A
B
C: тогда AB=AC=BC=0 и AD=BD=CD=a
- A
B и C
D тогда AB=CD=0 и AC=AD=BC=CD=a
- A
B: тогда A, C, D должны образовывать равносторонний треугольник и AB=0 и AC=AD=BC=BD=CD=a. (рис.9)
Рис.9. Совпадающие точки
Подведём итог:
Количество коротких расстояний, Количество длинных расстояний, Отношение между длинными и короткими расстояниями
5 1 1:sqrt(3)
4 2 1:sqrt(2+sqrt(3))
2 4 1:sqrt(2+sqrt(3))
4 2 1:sqrt(2)
3 3 1:sqrt(3)
3 3 1:(1+sqrt(5))/2
С совпадающими точками
3 3 0:любое
2 4 0: любое
1 5 0: любое
Видео:№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

Могут ли 4 точки на плоскости быть вершинами разных четырёхугольников
Ответ оставил Гость
прийдется дать ответ. решение смотри в файле
Поделись вопросом в социальных сетях!
Если Вы не получили ответ на свой вопрос, то предлагаем воспользоваться поиском, чтобы найти похожие вопросы и ответы по предмету -> Геометрия. А если Вы знаете правильный ответ сами, то будем признательны если Вы ответите, воспользовавшись формой ниже.
🎬 Видео
№5. Докажите, что через три данные точки, лежащие на прямой, проходит плоскость.Скачать

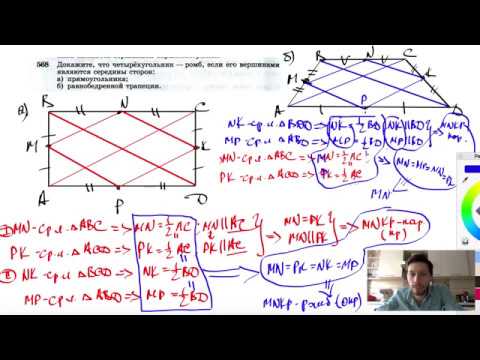
№568. Докажите, что четырехугольник — ромб, если его вершинами являются середины сторон:Скачать
Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Как проверить лежат ли 4 точки в одной плоскости Аналитическая геометрияСкачать

№3. Верно ли, что: а) любые три точки лежат в одной плоскости;Скачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

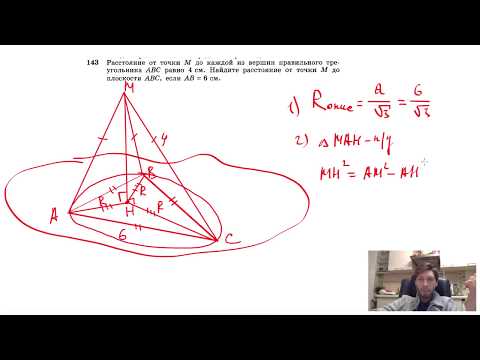
№143. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 смСкачать
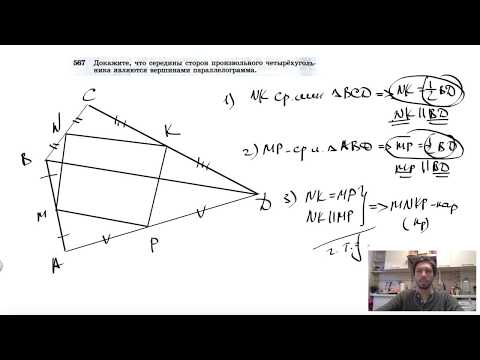
№567. Докажите, что середины сторон произвольного четырехугольника являютсяСкачать
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

10 класс, 14 урок, Задачи на построение сеченийСкачать

Параллельные прямые | Математика | TutorOnlineСкачать

ЛоманаяСкачать

Ломаные и многоугольники | Задачи 1-10 | Решение задач | Волчкевич | Уроки геометрии в задачахСкачать

Ломаные, многоугольники №1-№8 | Волчкевич, Уроки геометрии в задачахСкачать









 B
B C: тогда AB=AC=BC=0 и AD=BD=CD=a
C: тогда AB=AC=BC=0 и AD=BD=CD=a B и C
B и C D тогда AB=CD=0 и AC=AD=BC=CD=a
D тогда AB=CD=0 и AC=AD=BC=CD=a B: тогда A, C, D должны образовывать равносторонний треугольник и AB=0 и AC=AD=BC=BD=CD=a. (рис.9)
B: тогда A, C, D должны образовывать равносторонний треугольник и AB=0 и AC=AD=BC=BD=CD=a. (рис.9)
