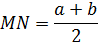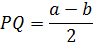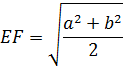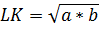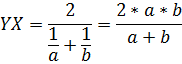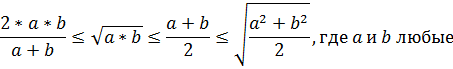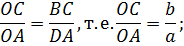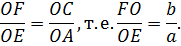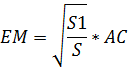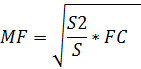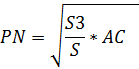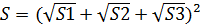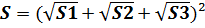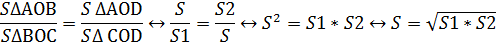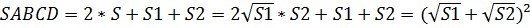Mn средняя линия трапеции abcd из точки м стороны ав проведена прямая параллельно боковой

Видео:СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ #математика #егэ #shorts #профильныйегэСкачать

Средняя линия МК трапеции АВСБ (ВС || АО) равна 56 см. Через середину М стороны АВ проведена прямая, которая параллельна стороне СБ и пересекает

Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Ваш ответ

Видео:8 класс, 49 урок, Средняя линия трапецииСкачать

решение вопроса

Видео:Трапеция. Средняя линия трапеции.Скачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,701
• разное 16,822

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Урок34. Трапеция Средняя линия трапеции (8 класс)Скачать

Mn средняя линия трапеции abcd из точки м стороны ав проведена прямая параллельно боковой

помогите решить срочно надо

2.плоскость альфа проходит через середины боковых сторон AB и CD трапеции. ABCD точки M и P.

а.)докажите, что AD параллельна альфу.

б.)найдите BC, если AD=10см, MP=8см.

Информация

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Видео:Средняя линия трапеции | Геометрия 7-9 класс #84 | ИнфоурокСкачать

Замечательные свойства трапеции

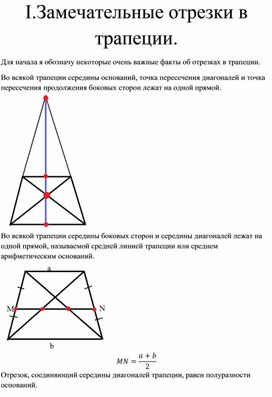
I .Замечательные отрезки в трапеции.

Для начала я обозначу некоторые очень важные факты об отрезках в трапеции.

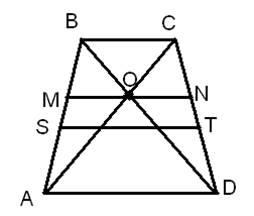
1. Во всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжения боковых сторон лежат на одной прямой.

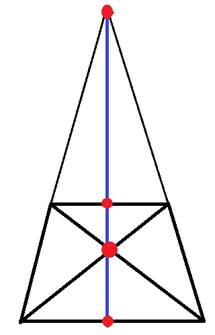
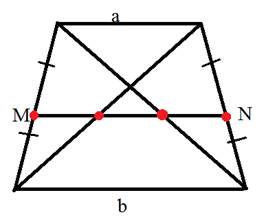
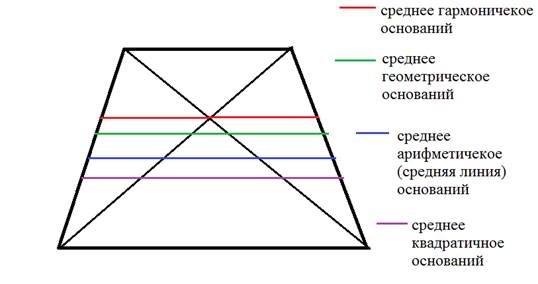
2. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой, называемой средней линией трапеции или среднем арифметическим оснований.

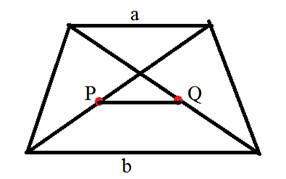
3. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.

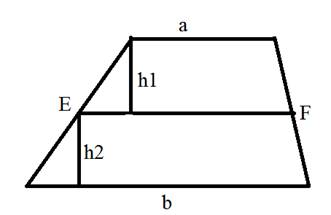
4. Отрезок, параллельный основаниям и разбивающий трапецию на две равновеликие трапеции, равен среднему квадратичному оснований:

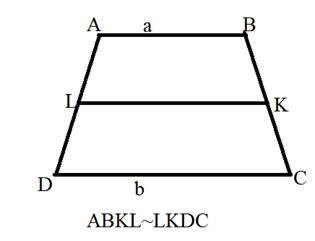
5. Отрезок,разбивающий трапецию на две подобные трапеции, имеет длину, равную среднему геометрическому длин оснований.

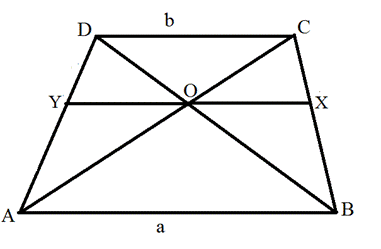
6. Отрезок, проходящий через точку пересечения диагоналей параллельно основаниям, равен среднему гармоническому оснований.

Между средними отрезками выполняются следующие соотношения

Доказательства этих фактов я не считаю нужным и уместным приводить в докладе, так как любой уважающий себя школьник должен их знать и уметь делать самостоятельно

Теперь, когда мы знаем эти, весьма важные, факты преступим к решению поистине прекрасных задач.

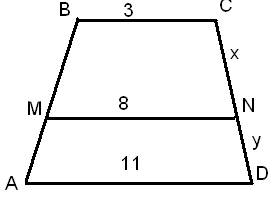
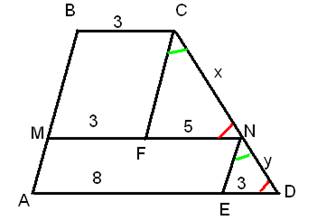
Задача 1 : ABCD — трапеция, отрезок MN параллелен основаниям трапеции; AD =11, BC =3, MN =8.Может ли быть x : y =4:3?

Применим приём достраивания.

Построим CF ║ BA , NE ║ BA . По построению MBCF и AMNE — параллелограммы, тогда имеем MF =3, FN =5, AE =8 и ED =3.

∆ END ( ∟ FCN =∟ END , ∟ FNC =∟ EDN , как накрестлежащие). Из подобия следует, что x : y =5:3, следовательно такого соотношения, как указанно в условии не может быть.

Ответ: не может быть.

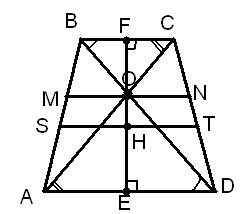
ABCD — трапеция, MN ║ AD , MN =4; точка О ,пересечения диагоналей, находится вдвое дальше от меньшего основания, чем от средней линии. Чему равны основания трапеции?

Пусть AD = a , BC = b .

1. Из 6 свойства трапеции, а именно, отрезок , проходящий через точку пересечения диагоналей параллельно основаниям, равен среднему гармоническому длин оснований трапеции. Следовательно, MN= .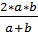

2. Пусть ST — средняя линия и через точку О проведена прямая EF , перпендикулярная к основаниям.

EF — высота трапеции, обозначим EF = h . Очевидно, что средняя линия делит высоту трапеции пополам EH = FH = 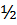h

∆ DOA (по двум накрестлежащим углам)→

∆ OEA (по двум углам)→

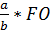
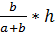
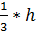
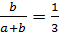
FO + OE = h , OE = , тогда находим FO = . По условию FH = FO +½ FO = FO , следовательно FO = и тогда , откуда имеем a =2 b .

3. Подставляем a =2 b в равенство 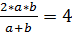, находим b =3 и а=6.

II Метод площадей

Для того, чтобы решать задачи, где рассматривается площадь трапеции, необходимо помнить несколько очень важных утверждений:

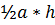
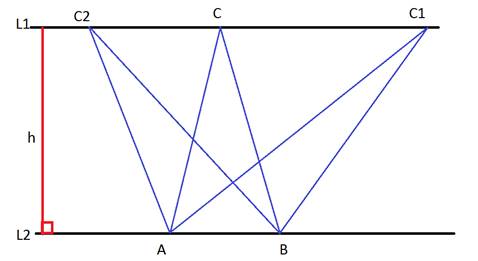
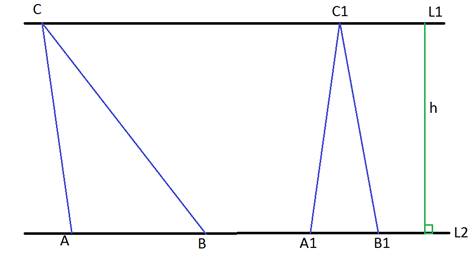
Это очень легко доказать: площадь треугольника можно вычислить по формуле . Высоты у всех треугольников одинаковы, так как расстояние между параллельными прямыми всегда одинаково; треугольники имеют общее основание. Из этих двух фактов следует, что S ∆ _ABC = S ∆ _{AC 1 B} = S ∆ _{AC 2 B} .

2. Если прямая L 1║ L 2 и треугольники не имеют общегооснования, то

.

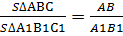
Высоты у этих треугольников равные, следовательно, площади этих треугольников относятся, как их снования.

А сейчас немного отвлечёмся от трапеции и перенесёмся в треугольник. Возьмём на рассмотрение одну очень красивую и важную задачу, которая поможет нам в понимании следующей задачи с трапецией. Когда я первый раз увидела эту задачу , она мне сразу же понравилась своей изящностью рисунка и простой гениальностью решения.

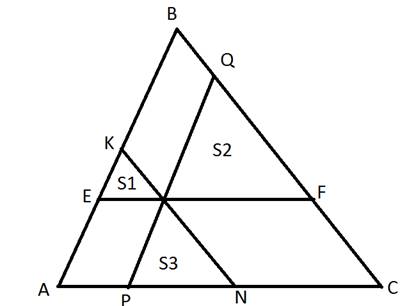
Через точку М, лежащую внутри треугольника АВС проведены три прямые, параллельные его сторонам. При этом образовались три треугольника(см.рис.), площади которых равны S 1, S 2, S 3. Найдите площадь треугольника АВС.

Легко видеть, что ∆ EKM ,∆ MQF и ∆ PMN подобны ∆АВС. Пусть S площадь треугольника АВС, тогда ; ; .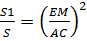

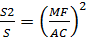
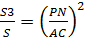
Так как EM=AP, MF=NC , то EM+PN+MF=AP+PN+NC=AC. Таким образом , 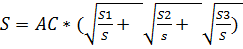, откуда следует

Ответ:

Мне захотелось убедиться, возможно ли в трапеции похожее соотношение площадей. И действительно в трапеции нашёлся похожий случай. Рассмотрим его в следующей задачи.

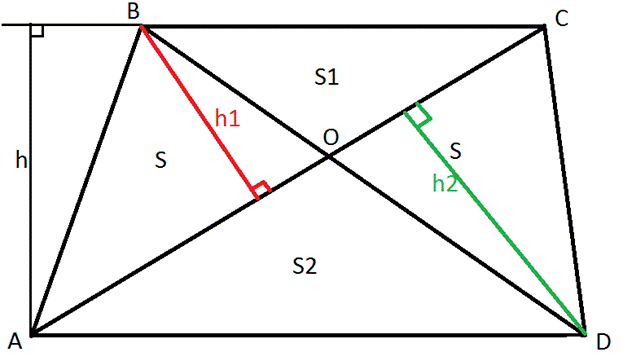
Дана трапеция ABCD ; в трапеции проведены диагонали, пересекающиеся в точке О. Выразите площадь трапеции из площадей образовавшихся треугольников.

1.Пусть площадь ∆ AOB и ∆ COD равны S . Площадь треугольника BOC равна S 1 , а площадь треугольника DOA равна S 2.

2. Докажем, что S ∆ _AOB = S ∆ _COD .

∆ ABC и ∆ DBC имеют общее основание BC и общую высоту h (т.к. BC ║ AD по свойству трапеции). Поскольку мы уже знаем , что треугольники имеющие общее основание и высоту имеют равные площади, следовательно, S ∆ _ABC = S ∆ _DBC . Заметим, что ∆ ABC и ∆ DBC имеют один общий элемент- ∆ BOC , следовательно, если вычесть из площадей искомых треугольников площадь ∆ BOC мы получим два, равных по площади треугольника. Значит, S ∆ _AOB = S ∆ _COD .

3. Рассмотрим ∆ AOB и ∆ BOC , они имеют общую высоту h 1, но имеют различные основания, поскольку мы знаем, что площади треугольников имеющих общую высоты относятся как их основания:

4. Рассмотрим ∆ AOD и ∆ COD , они имеют общую высоту h 2, но имеют различные основания, поскольку мы знаем, что площади треугольников имеющих общую высоты относятся как их основания:

5. Правые части равенств (1) и (2) одинаковы, следовательно одинаковы и правые части:

Ответ: площадь трапеции равна .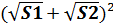

🎬 Видео

Средняя линия описанной трапеции. ВЫ ТОЧНО ПОПАЛИ!Скачать

Геометрия. 8 класс. Средняя линия трапеции /15.10.2020/Скачать

88. Средняя линия трапецииСкачать

Задание 3 ЕГЭ по математике. Урок 41Скачать

Геометрия 8. Средняя линия трапеции. Средняя линия треугольника. Задачи.Скачать

№30. Основание АВ трапеции ABCD параллельно плоскости α, а вершина С лежитСкачать

Треугольники №15. Средняя линия. Средняя линия трапеции №17. Равносторонний треугольник. (ОГЭ)Скачать

№346. Точки М и N — середины оснований АВ и CD трапеции ABCD, а О — произвольнаяСкачать

Теорема о средней линии трапецииСкачать

Геометрия 8. Урок 7 - Средняя линия треугольника и трапецииСкачать

№20. Средняя линия трапеции лежит в плоскости α. Пересекают ли прямые,Скачать

ТРАПЕЦИЯ . §8 геометрия 8 классСкачать

Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Решение задания №24 варианта 1 из ОГЭ по математике Ященко 36 вариантов ФИПИ 2023 Ответы ГДЗСкачать