Серединные перпендикуляры к сторонам ab и cd четырехугольника abcd

Вопрос по геометрии:

Серединные перпендикуляры к сторонам AB и CD четырехугольника ABCD пересекаются на стороне AD . Докажите, что если углы A и D четырехугольника ABCD равны, то его диагонали AC и BD также равны.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Проведём из вершины С прямую СЕ, из вершины В прямую ВЕ(смотри рисунок). Поскольку СN=NД и ЕN перпендикуляр к СД, то треугольник СЕД равнобедренный и ЕС =ЕД. Аналогично АЕ=ВЕ. Отсюда равны углы ВЕА и СЕД. Далее рассматриваем треугольники АЕС и ВЕД. Они равны по двум сторонам и углу между ними, следовательно против равных углов у них лежат равные стороны и АС=ВД.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:№681. Серединный перпендикуляр к стороне АВ равнобедренного треугольника ABC пересекаетСкачать

Серединные перпендикуляры к сторонам ABи CDчетырехугольника ABCD пересекаются на стороне AD?

Геометрия | 5 — 9 классы

Серединные перпендикуляры к сторонам ABи CDчетырехугольника ABCD пересекаются на стороне AD.

Докажите, что если углы Aи Dчетырехугольника ABCD равны, то его диагонали ACи BD также равны.

Проведём из вершины С прямую СЕ, из вершины В прямую ВЕ(смотри рисунок).

Поскольку СN = NД и ЕN перпендикуляр к СД, то треугольник СЕД равнобедренный и ЕС = ЕД.

Аналогично АЕ = ВЕ.

Отсюда равны углы ВЕА и СЕД.

Далее рассматриваем треугольники АЕС и ВЕД.

Они равны по двум сторонам и углу между ними, следовательно против равных углов у них лежат равные стороны и АС = ВД.

Видео:8 класс, 36 урок, Свойства серединного перпендикуляра к отрезкуСкачать

В ромбе ABCD диагонали пересекаются в точке О?

В ромбе ABCD диагонали пересекаются в точке О.

OM, OK, OE перпендикуляры , опущенные на стороны AB, BC, CD соответственно.

Докажите, что OM = OK и найдите сумму углов MOB и COE.

Видео:№680. Серединные перпендикуляры к сторонам АВ и АС треугольника ABC пересекаются в точке DСкачать

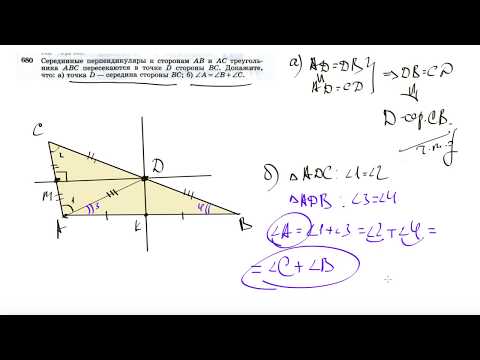
Биссектрисы углов C и D параллелограма ABCD пересекаются в точке K стороны AB?

Биссектрисы углов C и D параллелограма ABCD пересекаются в точке K стороны AB.

Докажите что K — середина AB.

Видео:Геометрия 8 класс (Урок№30 - Свойство серединного перпендикуляра.)Скачать

Биссектрисы углов B и C параллелограмма ABCD пересекаются в точке M стороны AD?

Биссектрисы углов B и C параллелограмма ABCD пересекаются в точке M стороны AD.

Докажите, что M — середина AD.

Видео:Биссектрисы пересекаются в одной точке| Задачи 28-33 | Решение задач | Волчкевич|Уроки геометрии 7-8Скачать

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке F стороны CD?

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке F стороны CD.

Докажите, что F — середина CD.

Видео:№679. Серединный перпендикуляр к стороне ВС треугольника ABC пересекает сторону АС в точке DСкачать

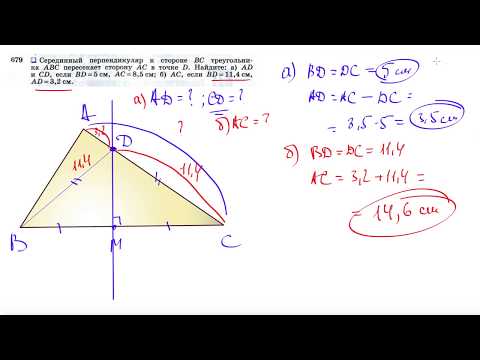
Вершины четырехугольника ABCDявляются серединами сторончетырехугольника, диагоналикоторого равны 6 дм ипересекаются под углом 60°?

Вершины четырехугольника ABCD

являются серединами сторон

которого равны 6 дм и

пересекаются под углом 60°.

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

В параллелограмме ABCD диагонали равны?

В параллелограмме ABCD диагонали равны.

Докажите что ABCD является прямоугольником.

Видео:#5warmup. Разбор пятой разминкиСкачать

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке F стороны CD?

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке F стороны CD.

Докажите, что F — середина CD.

Видео:Геометрия Серединный перпендикуляр диагонали AC прямоугольника ABCD пересекает сторону AB в точке MСкачать

Точка Т середина стороны СD квадрата ABCD диагонали которого пересекаются в точке О?

Точка Т середина стороны СD квадрата ABCD диагонали которого пересекаются в точке О.

Докажите что треугольник OTC подобен треугольнику ADC.

Видео:Вписанные углы | Задачи 31-37 | Решение задач | Волчкевич | Уроки геометрии 7-8 классыСкачать

Помогите решить?

Вершины четырёхугольника ABCD являются серединами сторон четырехугольника , диагонали которого равны по 6 дм и пересекаются под углом 60°.

Вычислите площадь четырёхугольника ABCD.

Видео:Признаки вписанного четырехугольника | Задачи 35-40 | Решение задач | Волчкевич |Уроки геометрии 7-8Скачать

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке F стороны CD?

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке F стороны CD.

Докажите, что F — середина CD.

Вы открыли страницу вопроса Серединные перпендикуляры к сторонам ABи CDчетырехугольника ABCD пересекаются на стороне AD?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 5 — 9 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

AC иBD — это диагонали параллелограмма. Если они равны, то это прямоугольник. Сторона AD — это катет треугольника ABD. По теореме Пифагора : AD = КореньBD ^ 2 — AB ^ 2 = Корень289 — 64 = Корень225 = 15 Следовательно, площадь ABCD = AB * AD = 8 * 1..

Диагональ в основании АС. АС = √2 * а Высота СС1 = АС = √2 * а Диагональ ВС1 — по т. Пифагора. ВС = √((a² + (√2a)²) = √(3 * a²) = √3 * a — ОТВЕТ Рисунок по ссылке. Http : / / SSMaker. Ru / 42a57dc9.

График : парабола, ветки которой направлены вниз ; пересекает ось Ох при у = 0 ; 4х — х² = 0 ; х(4 — х) = 0 ; х1 = 0 ; х2 = 4. Значения 0 и 4 являются пределами интеграла По формуле Ньютона — Лейбница S = интеграл(4х — х²)dх = (4х² / 2 — х³ / 3) — (..

5. Дано : | Решение ABCD — парал — м, |ВС = AD(по св — вам парал — м) = >AD = 6 см ВС = 6см, | угол ABK = 180 — (90 + 30) = 60гр(т. К. BK | перпенд. Угол КАВ = 30 гр | угла В) = >BK = 1 / 2 AB = >2х2 = 4 см = AB ВК перпендикуляр угла В | = > СD = 4..

Ты какой класс 7 — — 8 — 9 — 10 — — 11.

S = a * a S = 1. 2 * 1. 2 = 1. 44 .

S = а * 4 s°12 * 4 = 56 ответ 56.

Sin(60°) = √3 / 2. Cos(60°) = 1 / 2. B = 46. A = 24. (b — a) / 2 = (46 — 24) / 2 = 11. C = 11÷1 / 2 = 22. P = 2•22 + 46 + 24 = 114.

150, 50, 10 всё очень легко.

Угол А + угол В = 62°, тогда угол МВА + угол ВАМ = 62° / 2 = 31°. Из треугольника АМВ : угол АМВ = 180° — 31° = 149°, поскольку самое углов треугольника равна 180°. Ответ : 149°.

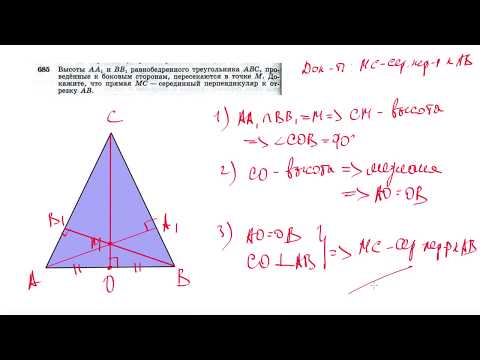
Видео:№685. Высоты АА1 и ВВ1 равнобедренного треугольника ABC, проведенные к боковым сторонамСкачать

Параллелограмм

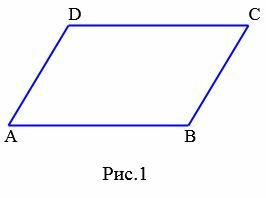
Определение 1. Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны.

На Рис.1 изображен параллелограмм поскольку ( small AB || CD, ;; AD || BC .)

Видео:Доказать, что точки лежат на одной окружностиСкачать

Свойства параллелограмма

Свойство 1. В параллелограмме противоположные углы равны и противоположные стороны равны.

Доказательство. Рассмотрим параллелограмм ABCD (Рис.2).

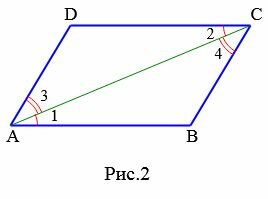Диагональ AC разделяют параллелограмм на два треугольника ACB и ACD. ( small angle 1=angle 2 ) поскольку эти углы накрест лежащие, при рассмотрении параллельных прямых AB и CD пересеченные секущей AC (см. теорему 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично ( small angle 3=angle 4 ), если рассмотреть параллельные прямые AD и BC пересеченные секущей AC. Тогда треугольники ACB и ACD равны по одной стороне и двум прилежащим углам: AC общая, ( small angle 1=angle 2 ), ( small angle 3=angle 4 ) (см. статью Треугольники. Признаки равенства треугольников). Поэтому ( small AB=CD, ;; AD=BC, ;; angle B=angle D. )

Из рисунка Рис.2 имеем: ( small angle A=angle 1+angle 3, ;; angle C=angle 2+angle 4. ) Учитывая, что ( small angle 1=angle 2 ) и ( small angle 3=angle 4 ), получим: ( small angle A=angle C. )

Свойство 2. Диагонали параллелограмма точкой пересечения разделяются пополам.

Доказательство. Рассмотрим параллелограмм ABCD (Рис.3) и пусть O точка пересечения диагоналей AC и BD. ( small angle 1=angle 2 ) поскольку эти углы накрест лежащие, при рассмотрении параллельных прямых AB и CD пересеченные секущей AC. ( small angle 3=angle 4 ), если рассмотреть параллельные прямые AB и CD пересеченные секущей BD. Поскольку в параллелограмме противоположные стороны равны: AB=CD (Свойство 1), то треугольники ABO и CDO равны по стороне и прилежашим двум углам. Тогда AO=OC и BO=OD.

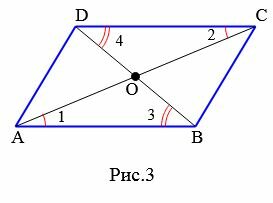Видео:Геометрия Серединный перпендикуляр диагонали BD параллелограмма ABCD пересекает стороныСкачать

Признаки параллелограмма

Признак 1. Если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник является параллелограммом.

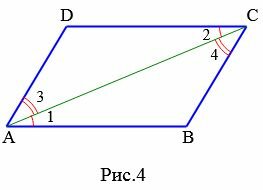Доказательство. Рассмотрим параллелограмм ABCD. Пусть AB=CD и AB || CD. Проведем диагональ AC (Рис.4). Поскольку AB || CD, то ( small angle 1=angle 2 ) как накрест лежащие углы − при рассмотрении параллельных прямых AB и CD пересеченных секущей AC. Тогда треугольники ACB и ACD равны, по двум сторонам и углу между ними. Действительно, AB=CD, AC− общая сторона ( small angle 1=angle 2 ). Но тогда ( small angle 3=angle 4. ) Рассмотрим прямые AD и BC, пересеченные секущей AC. Поскольку ( small angle 3 ) и ( small angle 4 ) являются накрест лежашими углами, то по теореме 1 статьи Параллельные прямые. Признаки параллельности прямых, эти прямые параллельны. Таким образом, в четырехугольнике противоположные стороны попарно параллельны (AB || CD, AD || BC) и, значит, данный четырехугольник параллелограмм.

Признак 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник является параллелограммом.

Доказательство. Рассмотрим параллелограмм ABCD (Рис.4). Проведем диагональ AC (Рис.4). Рассмотрим треугольники ACB и ACD. Эти треугольники равны по трем сторонам (см. статью Треугольники. Признаки равенства треугольников). Действительно. AC − общая для этих треугольников и по условию AB = CD, AD = BC. Тогда ( small angle 1=angle 2 ). Отсюда следует AB || CD. Имеем, AB = CD, AB || CD и по признаку 1 четырехугольник ABCD является параллелограммом.

Признак 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения разделяются пополам, то данный четырехугольник − параллелограмм.

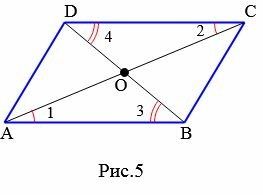Доказательство. Рассмотрим четырехугольник ABCD (Рис.5). Пусть диагонали четырехугольника пересекаются в точке O и точкой пересечения делятся пополам:

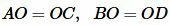Углы AOB и COD вертикальные, следовательно ( small angle AOB=angle COD ). Тогда треугольники AOB и COD равны по двум сторонам и углу меду ними:

,

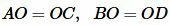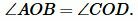Тогда AB = CD и ( small angle 1=angle 2 ). Но по признаку параллельности прямых следует, что AB || CD (теорема 1 статьи Параллельные прямые. Признаки параллельности прямых). Получили:

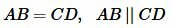и, по признаку 1 четырехугольник ABCD − параллелограмм.

💡 Видео

Высота, биссектриса, медиана. 7 класс.Скачать

Биссектрисы пересекаются в одной точке| Задачи 1-10 | Решение задач | Волчкевич| Уроки геометрии 7-8Скачать

#58. Олимпиадная задача о четырехугольникеСкачать

Вариант ФИПИ #11 все задачи (математика ОГЭ)Скачать

РЕШЕНИЕ ЗАДАЧИ ПО ТЕМЕ «СЕРЕДИННЫЙ ПЕРПЕНДИКУЛЯР». Задачи | ГЕОМЕТРИЯ 7 классСкачать

Этот четырёхугольник не то, чем кажется (ДВИ, Мехмат, 1970)Скачать