Неравнобедренный треугольник ось симметрии (3 видео)

Неравнобедренный треугольник ось симметрии

Пусть ABC — произвольный треугольник (рис.1 или 2 или 3); проведем биссектрису угла C, затем ось симметрии стороны AB (т.е. прямую, перпендикулярную к AB в середине M отрезка AB) и рассмотрим различные случаи взаимного расположения этих прямых; так как в рассуждениях участвуют только одна биссектриса и одна ось симметрии, то разрешим себе их называть просто «биссектриса» и «ось».

Случай 1: биссектриса и ось не пересекаются ,
т.е. либо параллельны, либо сливаются. Так как ось перпендикулярна к AB, т.е. совпадает с высотой, а в таком случае треугольник ABC — равнобедренный (CA=CB).

Случай 2: биссектриса и ось не пересекаются внутри
треугольника ABC
(рис.1), пусть в точке N. Так как эта точка равноудалена от сторон угла ACB, то, опустив из нее перпендикуляры NP и NQ соответственно на CB и CA, имеем NP=NQ. 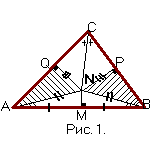Но точка N в тоже время равноудалена от концов отрезка AB, т.е. NB=NA. Прямоугольные треугольники NPB и NQA равны по катету и гипотенузе, следовательно, угол NAQ равен углу NBP. Прибавляя к этим равным углам равные между собой (как углы при основании равнобедренного треугольника ANB) углы NAB и NBA, получим угол CAB, равный углу CBA, значит, треугольник ABC — равнобедренный (именно CA=CB).

Случай 3: биссектриса и ось пересекаются на стороне AB ,
т.е. в середине M этой стороны. Это означает, что в треугольнике ABC медиана и биссектриса, проведенные из вершины C, совпадают, а отсюда следует, что этот треугольник- равнобедренный.

Замечание.
Предостерегаем читателя от возможной ошибки. Хорошо известно, что в равнобедренном треугольнике медиана и биссектриса совпадают. Но мы ссылаемся здесь не не это, а на обратное утверждение: «если в треугольнике медиана и биссектриса , проведенные из одной вершины, совпадают, то треугольник — равнобедренный». В такой формулировке обратная теорема также верна, но доказательство ее может затруднить читателя, поэтому приводим одно из возможных. Пусть в треугольнике ABC отрезок CM — одновременно медиана и биссектриса. Опустив из точки M перпендикуляры MP и MQ на стороны CB и CA (можно воспользоваться рис. 1, считая там точки M и N совпадающими; при этом прямая MN становится лишней), получаем равные прямоугольные треугольники MPB и MQA, а затем из равенства углов MBP и MAQ заключаем, что треугольник ABC — равнобедренный. Это рассуждение будет неполным, если не показать, что точки P и Q попадут именно на стороны CB и CA, а не на их продолжения. Одна из точек могла бы попасть на продолжение соответсвующей стороны, если бы один из углов A и B был тупым. Пусть, например, угол B — тупой, так что точка P лежит на продолжении стороны CB; по-прежнему получается угол MAQ равен углу MBP, но теперь это приводит к противоречию, так как первый из этих углов — внутренний для треугольника ABC, а второй — внешний, с первым не смежный.

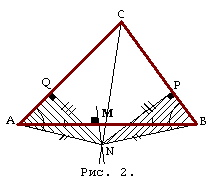
Случай 4а: биссектриса и ось пересекаются вне треугольника ABC; перпендикуляры, опущенные из точки N пересечения на стороны CB и CA, падают на эти стороны (рис. 2), а не на их продолжения.
Как и раньше, получаем равные треугольники NPB и NQA, равнобедренный треугольникANB. Углы при основании AB треугольника ABC равны теперь как разности (а не как суммы в случае 2) соответственно равных углов.

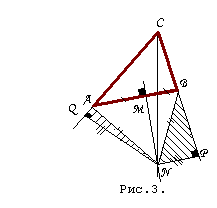
Случай 4б: биссектриса и ось пересекаются вне треугольника ABC; перпендикуляры, опущенные из точки N переечения на стороны CB и CA , падают на продолжение этих сторон (рис. 3).
Те же построения и рассуждения приводят к выводу о равенстве внешних углов при вершинах A и B треугольника ABC. Отсюда сейчас же вытекает равенство внутренних углов A и B, следовательно, CA=CB.

Анализ примера.
Рассмотрены не все возможные случаи (Здесь и дальше, говоря о возможных допущениях или о возможных случаях, мы вовсе не утверждаем, что все они действительно возможны в условиях данного примера. Наоборот, не раз случается, что допущенный нами сначала в качестве возможного случай потом окажется фиктивным, т.е. противоречащим условию или тому, что считается установленным, как это часто бывает в доказательствах «от противного». Таким образом, речь идет всегда о так называемых «априорных возможностях » (от a priori- заранее), т.е. о возможностях, которые представляются заранее, до учета остальных условий вопроса. ), именно не учтена возможность того, что из двух перпендикуляров NP и NQ один упадет на сторону треугольника ABC, а другой — на продолжение стороны (рис. 4, где пока не надо принимать во внимание окружность). Если это произойдет, то один из углов при основании AB треугольника ABC окажется разностью двух углов, а другой будет смежным для суммы тех же углов — отсюда, разумеется, никаких выводов, относящихся к углам при основании, а значит, и к равенству боковых сторон, сделать нельзя. Достаточно установить этот пробел в доказательстве, для того чтобы оно было опорочено. Более того, если данный треугольник — неравнобедренный, то можно утверждать (рассуждая от противного), что все рассмотренные случаи (рис. 1, 2 и 3) невозможны, а единственно возможный случай (рис. 4) упущен.

Содержание

Что такое симметрия и асимметрия?
Что означает симметрия в разных науках?
Как определяют симметрию разные словари?
Когда говорят об асимметрии?
О центральной и осевой симметрии
Какие фигуры являются симметричными?
Осевая и центральная симметрия
Что такое симметрия
Осевая симметрия
Центральная симметрия
Задачи на самопроверку
📺 Видео

Видео:Осевая симметрия. 6 класс.Скачать

Что такое симметрия и асимметрия?

Симметрия ассоциируется с гармонией и порядком. И не зря. Потому что на вопрос, что такое симметрия, есть ответ в виде дословного перевода с древнегреческого. И получается, что она означает соразмерность и неизменность. А что может быть упорядоченней, чем строгое определение местоположения? И что можно назвать более гармоничным, чем то, что строго соответствует размерам?

Видео:Математика 5 класс. Ось симметрии фигурыСкачать

Что означает симметрия в разных науках?

Биология. В ней важной составляющей симметрии является то, что животные и растения имеют закономерно расположенные части. Причем в этой науке не существует строгой симметрии. Всегда наблюдается некоторая асимметрия. Она допускает то, что части целого не совпадают с абсолютной точностью.

Физика. Система тел и изменения в ней описываются с помощью уравнений. В них оказываются симметричные составляющие, что позволяет упростить все решение. Это выполняется благодаря поиску сохраняющихся величин.

Математика. Именно в ней в основном и дается разъяснение, что такое симметрия. Причем большее значение ей уделяется в геометрии. Здесь симметрия — это способность к отображению у фигур и тел. В узком смысле она сводится просто к зеркальному отображению.

Видео:Ось симметрииСкачать

Как определяют симметрию разные словари?

В какой бы из них мы ни заглянули, везде встретится слово «соразмерность». У Даля можно увидеть еще и такое толкование, как равномерие и равнообразие. Другими словами, симметричное — значит одинаковое. Здесь же говорится о том, что она скучна, интереснее смотрится то, в чем ее нет.

На вопрос, что такое симметрия, словарь Ожегова уже говорит об одинаковости в положении частей относительно точки, прямой или плоскости.

В словаре Ушакова упоминается еще и пропорциональность, а также полное соответствие двух частей целого друг другу.

Видео:Центральная симметрия. 6 класс.Скачать

Когда говорят об асимметрии?

Приставка «а» отрицает смысл основного существительного. Поэтому асимметрия означает то, что расположение элементов не поддается определенной закономерности. В ней отсутствует всякая неизменность.

В живой природе асимметрия играет важную роль. Причем она может быть как полезной, так и вредной. К примеру, сердце помещается в левую половину груди. За счет этого левое легкое существенно меньшего размера. Но это необходимо.

Видео:Оси симметрии прямоугольника, равнобедренного треугольника, окружностиСкачать

О центральной и осевой симметрии

В математике выделяют такие ее виды:

центральная, то есть выполненная относительно одной точки;
осевая, которая наблюдается около прямой;
зеркальная, она основывается на отражениях;
симметрия переноса.

Что такое ось и центр симметрии? Это точка или прямая, относительно которой любой точке тела найдется другая. Причем такая, чтобы расстояние от исходной до получившейся делилось пополам осью или центром симметрии. Во время движения этих точек они описывают одинаковые траектории.

В ситуациях, когда необходимо найти центр симметрии, нужно поступать следующим образом. Если фигур две, то найти у них одинаковые точки и соединить их отрезком. Потом разделить пополам. Когда фигура одна, то помочь может знание ее свойств. Часто этот центр совпадает с точкой пересечения диагоналей или высот.

Видео:Фигуры с осью симметрии.Геометрия 8 класс. Глава 5Скачать

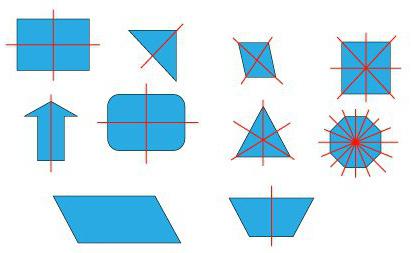
Какие фигуры являются симметричными?

Геометрические фигуры могут обладать осевой или центральной симметрией. Но это не обязательное условие, существует множество объектов, которые не обладают ею вовсе. К примеру, параллелограмм обладает центральной, но у него нет осевой. А неравнобедренные трапеции и треугольники не имеют симметрии совсем.

Если рассматривается центральная симметрия, фигур, обладающих ею, оказывается довольно много. Это отрезок и круг, параллелограмм и все правильные многоугольники с числом сторон, которое делится на два.

Центром симметрии отрезка (также круга) является его центр, а у параллелограмма он совпадает с пересечением диагоналей. В то время как у правильных многоугольников эта точка тоже совпадает с центром фигуры.

Если в фигуре можно провести прямую, вдоль которой ее можно сложить, и две половинки совпадут, то она (прямая) будет являться осью симметрии. Интересно то, сколько осей симметрии имеют разные фигуры.

К примеру, острый или тупой угол имеет только одну ось, которой является его биссектриса.

Если нужно найти ось в равнобедренном треугольнике, то нужно провести высоту к его основанию. Линия и будет осью симметрии. И всего одной. А в равностороннем их будет сразу три. К тому же, треугольник обладает еще и центральной симметрией относительно точки пересечения высот.

У круга может быть бесконечное число осей симметрии. Любая прямая, которая проходит через его центр, может исполнить эту роль.

Прямоугольник и ромб обладают двумя осями симметрии. У первого они проходят через середины сторон, а у второго совпадают с диагоналями.

Квадрат же объединяет предыдущие две фигуры и имеет сразу 4 оси симметрии. Они у него такие же, как у ромба и прямоугольника.

Видео:Прямоугольник. Ось симметрии. 5 классСкачать

Осевая и центральная симметрия

О чем эта статья:

Видео:У равнобедренного треугольника есть ось симметрии. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

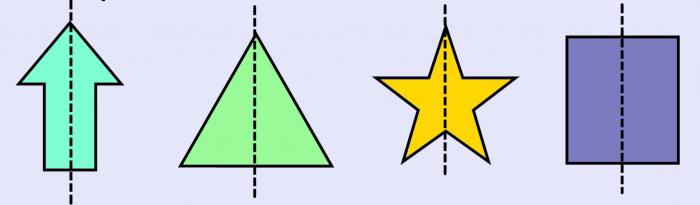
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

Ось симметрии угла — биссектриса.
Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
Оси симметрии прямоугольника проходят через середины его сторон.
У ромба две оси симметрии — прямые, содержащие его диагонали.
У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Видео:Осевая и центральная симметрия, 6 классСкачать

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
С другой стороны прямой отложим такие же расстояния.
Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
Измеряем расстояние от вершин до точек на прямой.
Откладываем такие же расстояния на другой стороне оси симметрии.
Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

Проводим через точку А прямую, перпендикулярную прямой l.
Проводим через точку В прямую, перпендикулярную прямой l.
Измеряем расстояния от точек А и В до прямой l.
Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Видео:ВПР 6 класс. 12 задание. Фигура симметиичная данной относительно оси.Скачать

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

Измеряем расстояние от точки B до точки О и от точки А до точки О.
Проводим прямую из точки А через точку О и выводим ее на другую сторону.
Проводим прямую из точки B через точку О и выводим ее на другую сторону.
Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.
Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Видео:Осевая симметрия, как начертить треугольники симметричноСкачать

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.