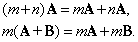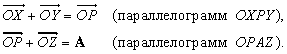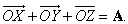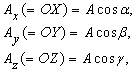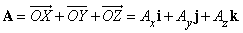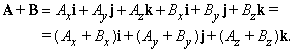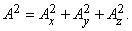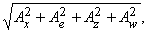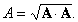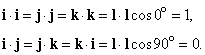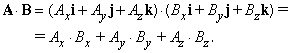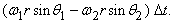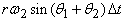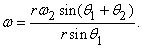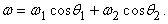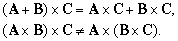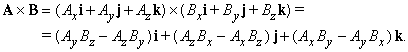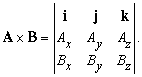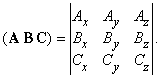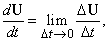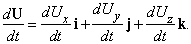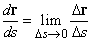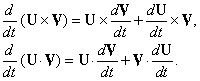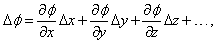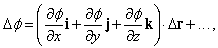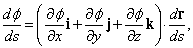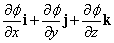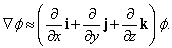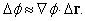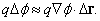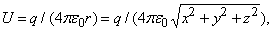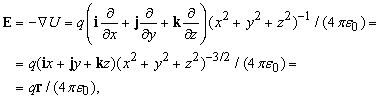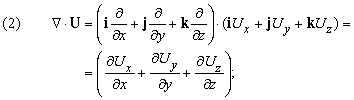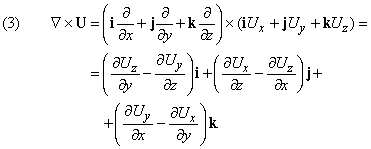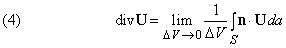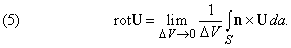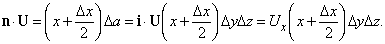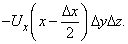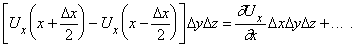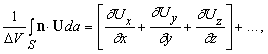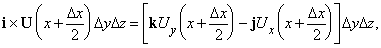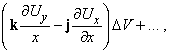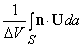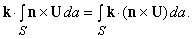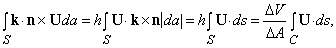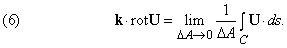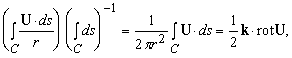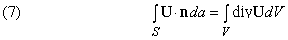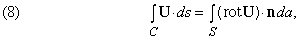Векторы в физике и математике

Одним из ключевых связующих звеньев между математикой и физикой является понятие векторной величины. Без знания векторной алгебры не может вообще идти речь о глубоком понимании многих разделов физики. Векторная алгебра является фундаментом, на котором построено все здание классической физики. Отсутствие на уроках математики задач физического содержания препятствует более успешному усвоению темы векторы, так как именно в физике тема изучается более углубленно, практически все физические задачи несут в себе понятие вектора.

Объектом исследования являются векторы и его свойства.

Предмет исследования: применение вектора и его свойств при решении задач школьного курса физики.

Цель работы:

— показать применение вектора и его свойств при решении физических задач школьного курса физики 7-11 классов, олимпиадных задач, а так же задач ЕГЭ;

— определить сущность, функции межпредметных связей и их классификацию, а так же повысить собственный уровень знаний и умений в применении свойств вектора при решении физических задач.

Видео:Физика | Ликбез по векторамСкачать

Скачать:

Предварительный просмотр:

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Подписи к слайдам:

в физике Векторы и математике у х А О В n

Объектом исследования являются Векторы и его свойства

Предмет исследования Применение вектора и его свойств при решении задач школьного курса физики

Цель работы -определить сущность, функции межпредметных связей и их классификацию, а так же повысить собственный уровень знаний и умений в применении свойств вектора при решении физических задач; -показать применение вектора и его свойств при решении физических задач школьного курса физики 7-11 классов, олимпиадных задач, а так же задач ЕГЭ;

Задачи 3. Решить задачи разного уровня сложности, содержащиеся в учебниках физики, сборниках задач, олимпиадных задач и задач ЕГЭ по выбранным темам. 1. Сопоставить понятие вектор, которое дается в учебниках школьного курса физики и геометрии; 2. Проанализировать содержание курса физики 7-11 классов и отобрать темы, в которых при решении задач используется свойства вектора;

Актуальность Необходимость формирования целостного представления о применении векторов в физике и математике и подготовки к ЕГЭ по этим предметам.

Практическая значимость работы Заключается в том, что предложенные в работе задачи могут быть использованы на уроках математики, быть полезными учащимся при изучении курса физики и подготовке к ЕГЭ, решении практических задач. Данная работа может представлять интерес для учителей физики и математики при подготовке к урокам и организации повторения.

Векторы в математике Впервые, понятие вектора дается на уроке геометрии в 8 классе учебника А. В. Погорелова. Вектором называют направленный отрезок, направление которого определяется указанием его начала и конца.

Векторы в математике Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающая вектор. Если начало вектора совпадает с его концом, такой вектор называется нулевым вектором. Нулевой вектор обозначается .

Векторы в математике Два вектора называются равными , если они совмещаются параллельным переносом. Равные векторы одинаково направлены и равны по абсолютной величине. Равные векторы имеют равные соответствующие координаты. m n

Действия над векторами сложение векторов умножение вектора на число скалярное произведение векторов разложение вектора по координатным осям

Сложение векторов Правило треугольника Правило параллелограмма

Умножение вектора на число ( λ =

Скалярное произведение векторов ( . ( = + Если скалярные векторы перпендикулярны, то их произведение равно нулю.

Разложение вектора по координатным осям Вектор называется единичным, если его абсолютная величина равна единице. Единичные векторы, имеющие направления координатных полуосей, называются координатными векторами. (1;0) (0;1) и ( λ + μ λ . μ

Векторы в физике В школьном курсе физики учебника А.В. Пёрышкина 7 класса, впервые понятие векторной величины вводится на примере таких физических величин, как Сила и Скорость . Так же вводится понятие Вес тела , которое тоже является векторной величиной. Болеет углубленно понятие вектора и его свойств затрагивается при изучении физики 9 класса учебника А. В. Пёрышкина и Е. М. Гутник .

Проекция вектора на ось Проекцией точки А на ось l называется число, соответствующее основанию перпендикуляра АВ, опущенного на ось l из точки А. Проекцией вектора на ось l называется разность проекций конца вектора и его начала.

Решение физических задач векторным методом Задача . С какого расстояния S от центра полусферы радиуса R =1,35 м, с какой скоростью и под каким углом β нужно бросить маленькую шайбу (из положения 1), чтобы она, попав на полусферу, остановилась на её вершине (положение 2) рисунок (а)? Трением шайбы о полусферу и сопротивлением воздуха пренебречь. Ускорение свободного падения считать равным 10 м/с 2 . Сформулируем обратную задачу : На каком расстоянии S от центра полусферы, с какой скоростью U и под каким углом β упадёт шайба, скатывающаяся с вершины полусферы радиуса R рисунок (б)? Трением шайбы о поверхность полусферы и сопротивлением воздуха пренебречь.

Решение физических задач векторным методом V 0 = . (1.1 ) Решение. mg cos α = m V 0 2 /R, откуда V 0 = . (1.2) h = R(1 – cos α) V 0 = . (1.3) cos α = 2/3 (1.4) V 0 = = = 3 м/с (1.5) Х = V ox t = ( V o cos α)t ( 1.6) Y = V oy t + gt 2 /2 = (V o sin α)t +gt 2 /2 ( 1.7) При t = t п – времени полёта шайбы до точки падения, X = X max , a Y = R cos α = 1,35 . 2/3 = 0,9 м sin α = = = = /3. ………………

Решение физических задач векторным методом 0,9 = t п + 5t п 2 , (1.8) t п = ( + )/ 10 = 0,7 с. X max = ( V o cos α)t п = 3 . 2/3 . 0,7 = 1,4 м. S = X max + R sin α = 1,4 + 1,35 . /3 = 2,41 м. V = ( 1.9). V ox = V o cos α = 3 . 2/3 = 2 м; V y = V o sin α + gt п = 3 . /3 + 10 . 0,7 = 9,24 м/с , V = = 9,45 м/с. tg β = V y / V ox = 9,24/ 2 = 4,62 β = 77,8 o .

Решение физических задач векторным метом Задача . Частица массы 2m налетает на неподвижную частицу массы m. После столкновения частицы разлетаются симметрично под углом 45 о к направлению начальной скорости, рисунок (а). Во сколько раз возросла суммарная кинетическая энергия после столкновения?

Решение. = .(1.1 ) p = (1.2) Е к = р 2 /4m = 2р 1 2 / 4m = р 1 2 / 2m . (1.3 ) Е к1 + Е к2 = (р 1 2 / 2m) + (p 2 2 / 4m) = 3p 1 2 /4m. (1.4) (Е к1 + Е к2 )/ Е к = 3p 1 2 2m / p 1 2 4m = 3/2 = 1,5. (1.7 ) Решение физических задач векторным метом

Решение физических задач векторным метом По двум длинным параллельным проводникам, расположенным на расстоянии r, текут токи I 1 и I 2 в направлениях, указанных на рисунке (а), на котором изображены сечения проводников плоскостью, перпендикулярной им. Определить индукцию магнитного поля в точке, находящейся на расстоянии r 1 от первого проводника и на расстоянии r 2 от второго. Задача . (а) (б)

Решение физических задач векторным метом Решение. В= (1.1 ) а cos α по той же теореме, но только для треугольника rr 1 r 2 : cos α = (r 1 2 + r 2 2 – r)/ 2r 1 r 2 . (1.2 ) В = (1.3) (а) (б)

Задачи из ЕГЭ по физике Через неподвижный блок переброшена нерастяжимая нить. На концах этой нити подвешены грузы равных масс М. На один из грузов поставили груз массой m . Определите ускорение движения грузов, силу натяжения нити, силу давления груза m на M , а также силу давления на ось блока. Массой блока и нити можно пренебречь. Задача .

Задачи из ЕГЭ по физике Решение. для тела 1 для тела 2 для тела m Найдем mg = a ( 2 M + m ) a = g . Из уравнения (1) T = Mg + Ma = . Из уравнения (3) сила давления P = mg — ma = mg — m = .

Задачи из ЕГЭ по физике = -2 T = 0 = 2 T

Задачи из ЕГЭ по физике При скоростном спуске лыжник скользил вниз по склону с углом наклона , не отталкиваясь палками. Коэффициент трения лыж о снег 0.1. Сила сопротивления воздуха пропорциональна квадрату скорости: F = k , где k =0.7 кг/м. Какова максимальная скорость лыжника, если его масса 100 кг? Задача.

Задачи из ЕГЭ по физике Решение. = k a = a ( t ) а= u ’( t )=0 =29,8 м/с

Задачи из ЕГЭ по физике Два небольших упругих шарика подвешены на нити =10 см и =5 см так, что они соприкасаются, линия их центров горизонтальна, а нити вертикальны. Масса шариков Шарик массой отклоняют на угол от вертикали отпускают. На какие углы отклонятся нити после абсолютно упругого соударения шариков? Задача.

Задачи из ЕГЭ по физике Решение. Из ∆ AOB OB = BD=OD-OB= cos α= (1) ; = / 2; ⟹ h = m /2⟹ = Рассмотрим систему, состоящую из двух шариков. = /2 = /2 + /2

Задачи из ЕГЭ по физике = ⟹ = и = = /(2 g ) cos = 1- =1- =1-( ) =1- = = 1- (1- cos α )= =38, cos =1- =1 — = 1- =1- 2gh = = 1- 4(1- cos α) ( = ⟹ = arccos =8,

Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

ВЕКТОР

ВЕКТОР. В физике и математике вектор – это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Их можно противопоставить другим величинам, таким, как масса, объем, давление, температура и плотность, которые можно описать обычным числом, и называются они «скалярами».

Векторная запись используется при работе с величинами, которые невозможно задать полностью с помощью обычных чисел. Например, мы хотим описать положение предмета относительно некоторой точки. Мы можем сказать, сколько километров от точки до предмета, но не можем полностью определить его местоположение, пока не узнаем направление, в котором он находится. Таким образом, местонахождение предмета характеризуется численным значением (расстоянием в километрах) и направлением.

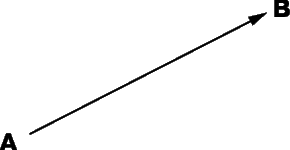
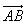
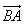
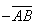
Графически векторы изображаются в виде направленных отрезков прямой определенной длины, как на рис. 1. Например, для того чтобы представить графически силу в пять килограммов, надо нарисовать отрезок прямой длиной в пять единиц в направлении действия силы. Стрелка указывает, что сила действует от A к B; если бы сила действовала от B к A, то мы бы записали или . Для удобства векторы обычно обозначаются полужирными прописными буквами (A, B, C и так далее); векторы A и –A имеют равные численные значения, но противоположны по направлению. Численное значение вектора А называется модулем или длиной и обозначается A или |A|. Это величина, конечно, скаляр. Вектор, начало и конец которого совпадают, называется нулевым и обозначается O.

Два вектора называются равными (или свободными), если их модули и направления совпадают. В механике и физике этим определением, однако, надо пользоваться с осторожностью, так как две равных силы, приложенные к различным точкам тела в общем случае будут приводить к различным результатам. В связи с этим векторы подразделяются на «связанные» или «скользящие», следующим образом:

Связанные векторы имеют фиксированные точки приложения. Например, радиус-вектор указывает положение точки относительно некоторого фиксированного начала координат. Связанные векторы считаются равными, если у них совпадают не только модули и направления, но они имеют и общую точку приложения.

Скользящими векторами называются равные между собой векторы, расположенные на одной прямой.

Видео:Вектор в Физике. Как Рисовать Вектор? Модуль Вектора || Урок Физики 8 класс // Подготовка к ЕГЭСкачать

Сложение векторов.

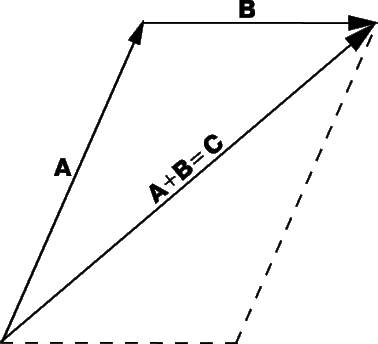
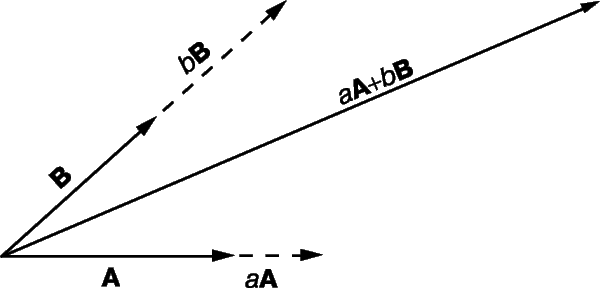
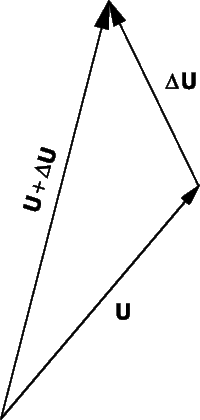
Идея сложения векторов возникла из того, что мы можем найти единственный вектор, который оказывает то же воздействие, что и два других вектора вместе. Если для того, чтобы попасть в некоторую точку, нам надо пройти сначала A километров в одном направлении и затем B километров в другом направлении, то мы могли бы достичь нашей конечной точки пройдя C километров в третьем направлении (рис. 2). В этом смысле можно сказать, что

Вектор C называется «результирующим вектором» A и B, он задается построением, показанным на рисунке; на векторах A и B как на сторонах построен параллелограмм, а C – диагональ, соединяющая начало А и конец В. Из рис. 2 видно, что сложение векторов «коммутативно», т.е.

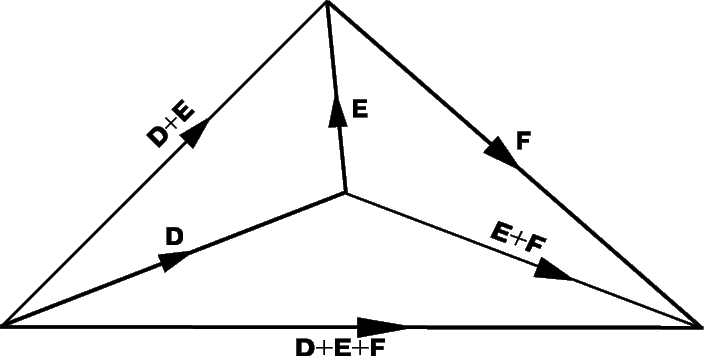
Аналогичным образом можно сложить несколько векторов, последовательно соединяя их «непрерывной цепочкой», как показано на рис. 3 для трех векторов D, E и F. Из рис. 3 также видно, что

т.е. сложение векторов ассоциативно. Суммировать можно любое число векторов, причем векторы необязательно должны лежать в одной плоскости. Вычитание векторов представляется как сложение с отрицательным вектором. Например,

где, как определялось ранее, –B – вектор, равный В по модулю, но противоположный по направлению.

Это правило сложения может теперь использоваться как реальный критерий проверки, является ли некоторая величина вектором или нет. Перемещения обычно подчиняются условиям этого правила; то же можно сказать и о скоростях; силы складываются таким же образом, как можно было видеть из «треугольника сил». Однако, некоторые величины, обладающие как численными значениями так и направлениями, не подчиняются этому правилу, поэтому не могут рассматриваться как векторы. Примером являются конечные вращения.

Видео:Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Умножение вектора на скаляр.

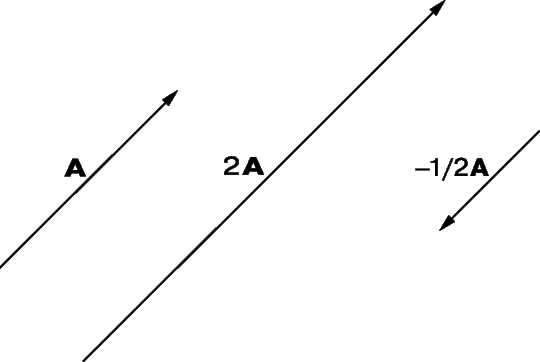
Произведение mA или Am, где m (m № 0) – скаляр, а A – ненулевой вектор, определяется как другой вектор, который в m раз длиннее A и имеет тоже направление что и A, если число m положительно, и противоположное, если m отрицательно, как показано на рис. 4, где m равно 2 и –1/2 соответственно. Кроме того, 1A = A, т.е. при умножении на 1 вектор не изменяется. Величина –1A – вектор, равный A по длине, но противоположный по направлению, обычно записывается как –A. Если А – нулевой вектор и(или) m = 0, то mA – нулевой вектор. Умножение дистрибутивно, т.е.

Мы можем складывать любое число векторов, причем порядок слагаемых не влияет на результат. Верно и обратное: любой вектор раскладывается на две или более «компоненты», т.е. на два вектора или более, которые, будучи сложенными, в качестве результирующего дадут исходный вектор. Например, на рис. 2, A и B – компоненты C.

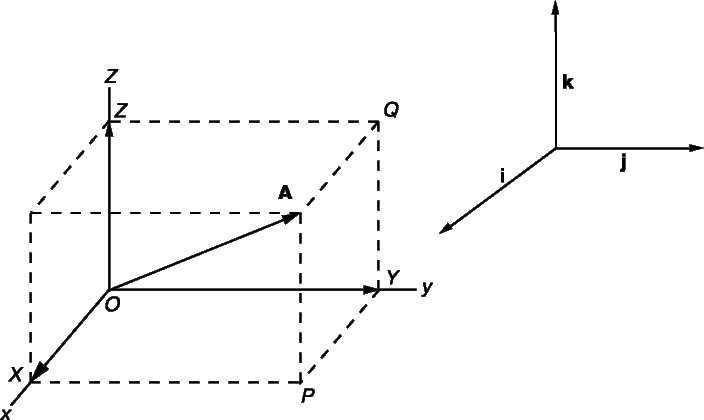
Многие математические действия с векторами упрощаются, если разложить вектор на три компоненты по трем взаимно перпендикулярным направлениям. Выберем правую систему декартовых координат с осями Ox, Oy и Oz как показано на рис. 5. Под правой системой координат мы подразумеваем, что оси x, y и z располагаются так, как могут быть расположены соответственно большой, указательный и средний пальцы правой руки. Из одной правой системы координат всегда можно получить другую правую систему координат соответствующим вращением. На рис. 5, показано разложение вектор A на три компоненты и . Они в сумме составляют вектор A, так как

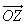
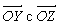
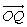
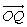
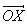
Можно было бы также сначала сложить и получить , а затем к прибавить .

Проекции вектора А на три координатные оси, обозначенные A_x, A_y и A_z называются «скалярными компонентами» вектора A:

где a , b и g – углы между A и тремя координатными осями. Теперь введем три вектора единичной длины i, j и k (орты), имеющие то же самое направление, что и соответствующие оси x, y и z. Тогда, если A_x умножить на i, то полученное произведение – это вектор, равный 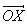, и

Два вектора равны тогда и только тогда, когда равны их соответствующие скалярные компоненты. Таким образом, A = B тогда и только тогда, когда A_x = B_x, A_y = B_y, A_z = B_z.

Два вектора можно сложить, складывая их компоненты:

Кроме того, по теореме Пифагора:

Видео:Векторы в физике. Что нужно знать? | 50 уроков физики (2/50)Скачать

Линейные функции.

Выражение aA + bB, где a и b – скаляры, называется линейной функцией векторов A и B. Это вектор, находящийся в той же плоскости, что A и B; если A и B не параллельны, то при изменении a и b вектор aA + bB будет перемещаться по всей плоскости (рис. 6). Если A, B и C не все лежат в одной плоскости, то вектор aA + bB + cC (a, b и c изменяются) перемещается по всему пространству. Предположим, что A, B и C – единичные векторы i, j и k. Вектор ai лежит на оси x; вектор ai + bj может перемещаться по всей плоскости xy; вектор ai + bj + ck может перемещаться по всему пространству.

Можно было бы выбрать четыре взаимно перпендикулярных вектора i, j, k и l и определить четырехмерный вектор как величину

а можно было бы продолжать до пяти, шести или любого числа измерений. Хотя визуально такой вектор представить невозможно, никаких математических трудностей здесь не возникает. Такая запись часто бывает полезна; например, состояние движущейся частицы описывается шестимерным вектором P (x, y, z, p_x, p_y, p_z), компоненты которого – ее положение в пространстве (x, y, z) и импульс (p_x, p_y, p_z). Такое пространство называется «фазовым пространством»; если мы рассматриваем две частицы, то фазовое пространство 12-мерное, если три, то 18-ти и так далее. Число размерностей можно неограниченно увеличивать; при этом величины, с которыми мы будем иметь дело, ведут себя во многом также, как те, которые мы рассмотрим в оставшейся части этой статьи, а именно, трехмерные векторы.

Видео:Урок 8. Векторные величины. Действия над векторами.Скачать

Умножение двух векторов.

Правило сложения векторов было получено путем изучения поведения величин, представленных векторами. Нет никаких видимых причин, по которым два вектора нельзя было бы каким-либо образом перемножить, однако это умножение будет иметь смысл только в том случае, если можно показать его математическую состоятельность; кроме того, желательно, чтобы произведение имело определенный физический смысл.

Существуют два способа умножения векторов, которые соответствуют этим условиям. Результатом одного из них является скаляр, такое произведение называется «скалярным произведением» или «внутренним произведением» двух векторов и записывается A Ч B или (A, B). Результатом другого умножения является вектор, называемый «векторным произведением» или «внешним произведением» и записывается A ґ B или [A, B]. Скалярные произведения имеют физический смысл для одного-, двух- или трех измерений, тогда как векторные произведения определены только для трех измерений.

Видео:ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Скалярные произведения.

Если под действием некоторой силы F точка, к которой она приложена, перемещается на расстояние r, то выполненная работа равна произведению r и компоненты F в направлении r. Эта компонента равна F cos б F, r с , где б F, r с – угол между F и r, т.е.

Произведенная работа = Fr cos б F, r с .

Это – пример физического обоснования скалярного произведения, определенного для любых двух векторов A, B посредством формулы

Так как все величины правой части уравнения – скаляры, то

следовательно, скалярное умножение коммутативно.

Скалярное умножение также обладает свойством дистрибутивности:

Если векторы A и B перпендикулярны, то cos б A, B с равен нулю, и, поэтому, A Ч B = 0, даже если ни A, ни B не равны нулю. Именно поэтому мы не можем делить на вектор. Допустим, что мы разделили обе части уравнения A Ч B = A Ч C на A. Это дало бы B = C, и, если бы можно было бы выполнить деление, то это равенство стало бы единственным возможным результатом. Однако, если мы перепишем уравнение A Ч B = A Ч C в виде A Ч (B – C) = 0 и вспомним, что (B – C) – вектор, то ясно, что (B – C) необязательно равен нулю и, следовательно, B не должен быть равным C. Эти противоречивые результаты показывают, что векторное деление невозможно.

Скалярное произведение дает еще один способ записи численного значения (модуля) вектора:

Скалярное произведение можно записать и другим способом. Для этого вспомним, что:

Поскольку последнее уравнение содержит x, y и z в качестве нижних индексов, уравнение, казалось бы, зависит от выбранной конкретной системы координат. Однако это не так, что видно из определения, которое не зависит от выбранных координатных осей.

Видео:ВЕКТОРЫ В МАТЕМАТИКЕ И ФИЗИКЕ | МАТЕМАТИКА | ОГЭ 2024 | МАСТЕР-ГРУППА | 99 БАЛЛОВСкачать

Векторные произведения.

Векторным или внешним произведением векторов называется вектор, модуль которого равен произведению их модулей на синус угла, перпендикулярный исходным векторам и составляющий вместе с ними правую тройку. Это произведение легче всего ввести, рассматривая соотношение между скоростью и угловой скоростью. Первая – вектор; мы теперь покажем, что последнюю также можно интерпретировать как вектор.

Угловая скорость вращающегося тела определяется следующим образом: выберем любую точку на теле и проведем перпендикуляр из этой точки до оси вращения. Тогда угловая скорость тела – это число радиан, на которые эта линия повернулась за единицу времени.

Если угловая скорость – вектор, она должна иметь численное значение и направление. Численное значение выражается в радианах в секунду, направление можно выбрать вдоль оси вращения, можно его определить, направив вектор в том направлении, в котором двигался бы правосторонний винт при вращении вместе с телом.

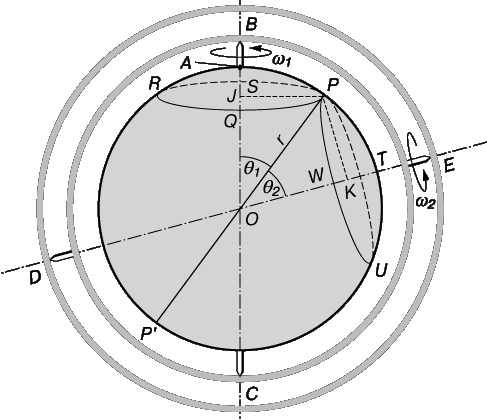
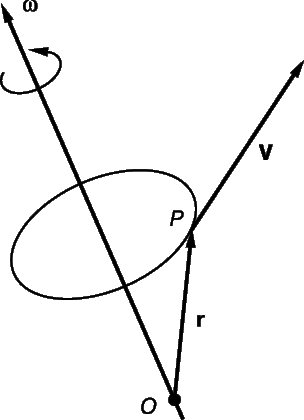
Рассмотрим вращение тела вокруг фиксированной оси. Если установить эту ось внутри кольца, которое в свою очередь закреплено на оси, вставленной внутрь другого кольца, мы можем придать вращение телу внутри первого кольца с угловой скоростью w 1 и затем заставить внутреннее кольцо (и тело) вращаться с угловой скоростью w 2. Рисунок 7 поясняет суть дела; круговые стрелки показывают направления вращения. Данное тело – это твердая сфера с центром О и радиусом r.

Придадим этому телу движение, которое является суммой двух различных угловых скоростей. Это движение довольно трудно представить наглядно, но достаточно очевидно, что тело больше не вращается относительно фиксированной оси. Однако все-таки можно сказать, что оно вращается. Чтобы показать это, выберем некоторую точку P на поверхности тела, которая в рассматриваемый нами момент времени находится на большом круге, соединяющем точки, в которых две оси пересекают поверхность сферы. Опустим перпендикуляры из P на оси. Эти перпендикуляры станут радиусами PJ и PK окружностей PQRS и PTUW соответственно. Проведем прямую POP ў , проходящую через центр сферы. Теперь точка P, в рассматриваемый момент времени одновременно перемещается по окружностям, которые соприкасаются в точке P. За малый интервал времени D t, P перемещается на расстояние

Это расстояние равно нулю, если

В этом случае точка P находится в состоянии мгновенного покоя, и точно также все точки на прямой POP ў . Остальная часть сферы будет в движении (окружности, по которым перемещаются другие точки, не касаются, а пересекаются). POP ў является, таким образом, мгновенной осью вращения сферы, подобно тому, как колесо, катящееся по дороге в каждый момент времени, вращается относительно своей нижней точки.

Чему равна угловая скорость сферы? Выберем для простоты точку A, в которой ось w 1 пересекает поверхность. В момент времени, который мы рассматриваем, она перемещается за время D t на расстояние

по кругу радиуса r sin w 1. По определению, угловая скорость

Из этой формулы и соотношения (1) мы получим

Другими словами, если записать численное значение и выбрать направление угловой скорости так, как это описано выше, то эти величины складываются как векторы и могут быть рассмотрены как таковые.

Теперь можно ввести векторное произведение; рассмотрим тело, вращающееся с угловой скоростью w . Выберем любую точку P на теле и любое начало координат О, которое находится на оси вращения. Пусть r – вектор, направленный от О к P. Точка P движется по окружности со скоростью

Вектор скорости V является касательным к окружности и указывает в направлении, показанном на рис. 8.

Это уравнение дает зависимость скорости V точки от комбинации двух векторов w и r. Используем это соотношение, чтобы определить новый вид произведения, и запишем:

Так как результатом такого умножения является вектор, это произведение названо векторным. Для любых двух векторов A и B, если

и направление вектора C таково, что он перпендикулярен плоскости, проходящей через А и B и указывает в направлении, совпадающем с направлением движения правовращающегося винта, если он параллелен C и вращается от A к B. Другими словами, мы можем сказать, что A, B и C, расположенные в таком порядке, образуют правый набор координатных осей. Векторное произведение антикоммутативно; вектор B ґ A имеет тот же модуль, что и A ґ B, но направлен в противоположную сторону:

Это произведение дистрибутивно, но не ассоциативно; можно доказать, что

Посмотрим, как записывается векторное произведение в терминах компонент и единичных векторов. Прежде всего, для любого вектора A,

Следовательно, в случае единичных векторов,

Это равенство также можно записать в виде определителя:

Если A ґ B = 0, то либо A или B равно 0, либо A и B коллинеарны. Таким образом, как и в случае скалярного произведения, деление на вектор невозможно. Величина A ґ B равна площади параллелограмма со сторонами A и B. Это легко видеть, так как B sin б A, B с – его высота и A – основание.

Существует много других физических величин, которые являются векторными произведениями. Одно из наиболее важных векторных произведений появляется в теории электромагнетизма и называется вектором Пойтинга P. Этот вектор задается следующим образом:

где E и H – векторы электрического и магнитного полей соответственно. Вектор P можно рассматривать как заданный поток энергии в ваттах на квадратный метр в любой точке. Приведем еще несколько примеров: момент силы F (крутящий момент) относительно начала координат, действующей на точку, радиус-вектор которой r, определяется как r ґ F; частица, находящаяся в точке r, массой m и скоростью V, имеет угловой момент mr ґ V относительно начала координат; сила, действующая на частицу, несущую электрический заряд q через магнитное поле B со скоростью V, есть qV ґ B.

Видео:Слив первого урока Основного курса Умскул | Введение. Математика в физике. Векторы для ОГЭСкачать

Тройные произведения.

Из трех векторов мы можем сформировать следующие тройные произведения: вектор (A Ч B) ґ C; вектор (A ґ B) ґ C; скаляр (A ґ B) Ч C.

Первый тип – произведение вектора C и скаляра A Ч B; о таких произведениях мы уже говорили. Второй тип называется двойным векторным произведением; вектор A ґ B перпендикулярен к плоскости, где лежат A и B, и поэтому (A ґ B) ґ C – вектор, лежащий в плоскости A и B и перпендикулярный C. Следовательно, в общем случае, (A ґ B) ґ C № A ґ (B ґ C). Записав A, B и C через их координаты (компоненты) по осям x, y и z и умножив, можно показать, что A ґ (B ґ C) = B ґ (A Ч C) – C ґ (A Ч B). Третий тип произведения, который возникает при расчетах решетки в физике твердого тела, численно равен объему параллелепипеда с ребрами A, B, C. Так как (A ґ B) Ч C = A Ч (B ґ C), знаки скалярного и векторного умножений можно менять местами, и произведение часто записывается как (A B C). Это произведение равно определителю

Заметим, что (A B C) = 0, если все три вектора лежат в одной и той же плоскости или, если А = 0 или (и) В = 0 или (и) С = 0.

Видео:ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

ДИФФЕРЕНЦИРОВАНИЕ ВЕКТОРА

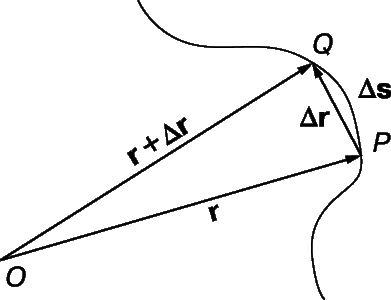
Предположим, что вектор U является функцией одной скалярной переменной t. Например, U может быть радиус-вектором, проведенным из начала координат до перемещающейся точки, а t – временем. Пусть t изменится на небольшую величину D t, что приведет к изменению U на величину D U. Это показано на рис. 9. Отношение D U/ D t – вектор, направленный в том же направлении, что и D U. Мы можем определить производную U по t, как

при условии, что такой предел существует. С другой стороны, можно представить U как сумму компонент по трем осям и записать

Если U – радиус-вектор r, то dr/dt – скорость точки, выраженная как функция времени. Продифференцировав по времени еще раз, мы получим ускорение. Предположим, что точка перемещается вдоль кривой, показанной на рис. 10. Пусть s – расстояние, пройденное точкой вдоль кривой. В течение малого интервала времени D t точка пройдет расстояние D s вдоль кривой; положение радиус-вектора изменится на D r. Следовательно D r/ D s – вектор направленный как D r. Далее

есть единичный вектор, касательный к кривой. Это видно из того, что при приближении точки Q к точке P, PQ приближается к касательной и D r приближается к D s.

Формулы для дифференцирования произведения подобны формулам для дифференцирования произведения скалярных функций; однако, так как векторное произведение антикоммутативно, порядок умножения должен быть сохранен. Поэтому,

Таким образом, мы видим, что, если вектор является функцией одной скалярной переменной, то мы можем представить производную почти также, как в случае скалярной функции.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Вектор и скалярные поля.

Видео:СЛОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

Градиент.

В физике часто приходится иметь дело с векторными или скалярными величинами, которые меняются от точки к точке в заданной области. Такие области называются «полями». Например, скаляр может быть температурой или давлением; вектор может быть скоростью движущейся жидкости или электростатическим полем системы зарядов. Если мы выбрали некоторую систему координат, то любой точке P (x, y, z) в заданной области соответствует некоторый радиус-вектор r (= xi + yj + zk) и также значение векторной величины U (r) или скаляра f (r), связанных с ним. Предположим, что U и f определены в области однозначно; т.е. каждой точке соответствует одна и только одна величина U или f , хотя различные точки могут, конечно, иметь различные значения. Допустим, что мы хотим описать скорость, с которой U и f изменяются при передвижении по этой области.

Простые частные производные, такие, как ¶ U/ ¶ x и ¶f / ¶ y, нас не устраивают, потому что они зависят от конкретно выбранных координатных осей. Однако можно ввести векторный дифференциальный оператор, независимый от выбора осей координат; этот оператор называется «градиентом».

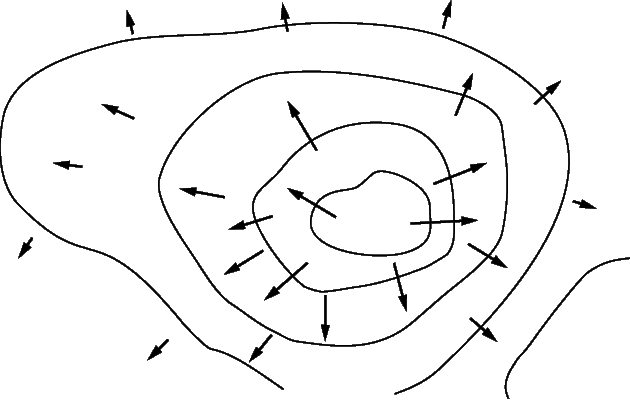
Пусть мы имеем дело со скалярным полем f . Сначала в качестве примера рассмотрим контурную карту области страны. В этом случае f – высота над уровнем моря; контурные линии соединяют точки с одним и тем же значением f . При движении вдоль любой из этих линий f не меняется; если двигаться перпендикулярно этим линиям, то скорость изменения f будет максимальной. Мы можем каждой точке сопоставить вектор, указывающий величину и направление максимального изменения скорости f ; такая карта и некоторые из этих векторов показаны на рис. 11. Если мы проделаем это для каждой точки поля, то получим векторное поле, связанное со скалярным полем f . Это поле вектора, называемого «градиентом» f , который записывается как grad f или Сf (символ С также называется «набла»).

В случае трех измерений, контурные линии становятся поверхностями. Малое смещение D r (= i D x + j D y + k D z) приводит к изменению f , которое записывается как

где точками обозначены члены более высоких порядков. Это выражение можно записать в виде скалярного произведения

Разделим правую и левую части этого равенства на D s, и пусть D s стремится к нулю; тогда

где dr/ds – единичный вектор в выбранном направлении. Выражение в круглых скобках – вектор, зависящий от выбранной точки. Таким образом, d f /ds имеет максимальное значение, когда dr/ds указывает в том же направлении, выражение, стоящее в скобках, является градиентом. Таким образом,

– вектор, равный по величине и совпадающий по направлению с максимальной скоростью изменения f относительно координат. Градиент f часто записывается в виде

Это означает, что оператор С существует сам по себе. Во многих случаях он ведет себя, как вектор, и фактически является «векторным дифференциальным оператором» – одним из наиболее важных дифференциальных операторов в физике. Несмотря на то, что С содержит единичные векторы i, j и k, его физический смысл не зависит от выбранной системы координат.

Какова связь между Сf и f ? Прежде всего предположим, что f определяет потенциал в любой точке. При любом малом смещении D r величина f изменится на

Если q – величина (например масса, заряд), перемещенная на D r, то работа, выполненная при перемещении q на D r равна

Так как D r – перемещение, то q Сf – сила; – Сf – напряженность (сила на единицу количества), связанная с f . Например, пусть U – электростатический потенциал; тогда E – напряженность электрического поля, задается формулой

Допустим, что U создается точечным электрическим зарядом в q кулонов, помещенным в начало координат. Значение U в точке P (x, y, z) с радиус-вектором r задается формулой

где e 0 – диэлектрическая постоянная свободного пространства. Поэтому

откуда следует, что E действует в направлении r и его величина равна q/(4 pe 0r 3 ).

Зная скалярное поле, можно определить связанное с ним векторное поле. Также возможно и обратное. С точки зрения математической обработки скалярными полями оперировать легче, чем векторными, так как они задаются одной функцией координат, в то время как векторное поле требует три функции, соответствующие компонентам вектора в трех направлениях. Таким образом, возникает вопрос: дано векторное поле, может ли мы записать связанное с ним скалярное поле?

Видео:10 класс, 38 урок, Понятие вектораСкачать

Дивергенция и ротор.

Мы видели результат действия С на скалярную функцию. Что произойдет, если С применить к вектору? Имеются две возможности: пусть U (x, y, z) – вектор; тогда мы можем образовать векторное и скалярное произведения следующим образом:

Первое из этих выражений – скаляр, называемый дивергенцией U (обозначается divU); второе – вектор, названный ротор U (обозначается rotU).

Эти дифференциальные функции, дивергенция и ротор, широко используются в математической физике.

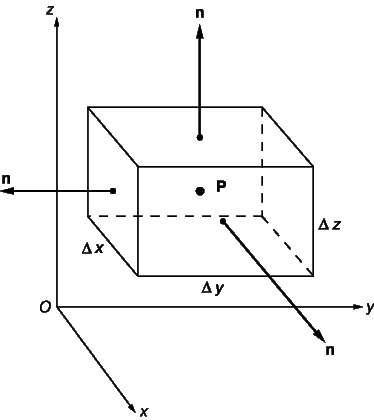
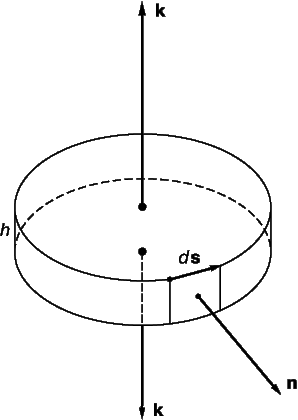
Представьте, что U – некоторый вектор и что он и его первые производные непрерывны в некоторой области. Пусть P – точка в этой области, окруженная малой замкнутой поверхностью S, ограничивающей объем D V. Пусть n – единичный вектор, перпендикулярный к этой поверхности в каждой точке (n меняет направление при движении вокруг поверхности, но всегда имеет единичную длину); пусть n направлен наружу. Покажем, что

Здесь S указывает, что эти интегралы берутся по всей поверхности, da – элемент поверхности S.

Для простоты мы выберем удобную для нас форму S в виде небольшого параллелепипеда (как показано на рис. 12) со сторонами D x, D y и D z; точка P – центр параллелепипеда. Вычислим интеграл из уравнения (4) сначала по одной грани параллелепипеда. Для передней грани n = i (единичный вектор параллелен оси x); D a = D y D z. Вклад в интеграл от передней грани равен

На противоположной грани n = –i; эта грань дает вклад в интеграл

Используя теорему Тейлора, получим общий вклад от двух граней

Заметим, что D x D y D z = D V. Аналогичным образом можно вычислить вклад от двух других пар граней. Полный интеграл равен

и если мы положим D V ® 0, то члены более высокого порядка исчезнут. По формуле (2) выражение в скобках – это divU, что доказывает равенство (4).

Равенство (5) можно доказать таким же образом. Воспользуемся снова рис. 12; тогда вклад от передней грани в интеграл будет равен

и, используя теорему Тейлора, получим, что суммарный вклад в интеграл от двух граней имеет вид

т.е. это два члена из выражения для rotU в уравнении (3). Другие четыре члена получатся после учета вкладов от других четырех граней.

Что, в сущности, означают эти соотношения? Рассмотрим равенство (4). Предположим, что U – скорость (жидкости, например). Тогда n Ч U da = U_n da, где U_nявляется нормальной компонентой вектора U к поверхности. Поэтому, U_n da – это объем жидкости, протекающей через da в единицу времени, а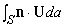 – это объем жидкости, вытекающей через S в единицу времени. Следовательно,

– скорость расширения единицы объема вокруг точки P. Отсюда дивергенция получила свое название; она показывает скорость, с которой жидкость расширяется из (т.е. расходится от) P.

Чтобы объяснить физическое значение ротора U, рассмотрим другой поверхностный интеграл по маленькому цилиндрическому объему высотой h, окружающему точку P; плоско-параллельные поверхности могут быть ориентированы в любом направлении, которое мы выбираем. Пусть k –единичный вектор перпендикулярный к каждой поверхности, и пусть площадь каждой поверхности D A; тогда полный объем D V = h D A (рис. 13). Рассмотрим теперь интеграл

Подынтегральное выражение – уже упоминавшееся ранее тройное скалярное произведение. Это произведение будет равно нулю на плоских поверхностях, где k и n параллельны. На кривой поверхности

где ds – элемент кривой как показано на рис. 13. Сравнивая эти равенства с соотношением (5), получаем, что

Мы по-прежнему предполагаем, что U – скорость. Чему в таком случае будет равна средняя угловая скорость жидкости вокруг k? Очевидно, что

если D A ® 0. Это выражение максимально, когда k и rotU указывают в одном и том же направлении; это означает, что rotU – вектор, равный удвоенной угловой скорости жидкости в точке P. Если жидкость вращается относительно P, то rotU № 0, и векторы U будут вращаться вокруг P. Отсюда и возникло название ротора.

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Теорема дивергенции (теорема Остроградского – Гаусса)

Теорема дивергенции (теорема Остроградского – Гаусса) является обобщением формулы (4) для конечных объемов. Она утверждает, что для некоторого объема V, ограниченного замкнутой поверхностью S,

и справедлива для всех непрерывных векторных функций U, имеющих непрерывные первые производные всюду в V и на S. Мы не будем приводить здесь доказательство этой теоремы, но ее справедливость можно понять интуитивно, представляя объем V разделенным на ячейки. Поток U через поверхность, общую для двух ячеек обращается в нуль, и только ячейки, находящиеся на границе S внесут вклад в поверхностный интеграл.

Видео:Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

Теорема Стокса

является обобщением уравнения (6) для конечных поверхностей. Она утверждает, что

где C – замкнутая кривая и S – любая поверхность, ограниченная этой кривой. U и ее первые производные должны быть непрерывны всюду на S и C.

Александров П.С. Лекции по аналитической геометрии. М., 1968
Погорелов А.В. Аналитическая геометрия, 3 изд. М., 1968

Видео:Все о векторах за 60 минут | Математика ОГЭ | Молодой РепетиторСкачать

Проектная работа. Вектор. 9 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:8 класс, 40 урок, Понятие вектораСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

МБОУ Одинцовская гимназия №13

Проектная работа по теме

Выполнили ученики 9А класса

Руководитель учитель математики

Что такое вектор и действия над векторами.

Векторы в геометрии, в физике, в других науках.

Векторы в повседневной жизни.

С уверенностью можно сказать, что мало кто из людей задумывается о том, что векторы окружают нас повсюду и помогают нам в повседневной жизни. Рассмотрим ситуацию: парень назначил девушке свидание в двухстах метрах от своего дома. Найдут ли они друг друга? Конечно, нет, так как юноша забыл указать главное: направление, то есть по-научному – вектор.

Далее, в процессе работы над данным проектом, Мы приведём ещё интересные примеры с векторами.

Вообще, мы считаем, что математика – это интереснейшая наука, в познании которой нет границ.

Мы выбрали тему о векторах не случайно, нас очень заинтересовало то, что понятие «вектор» выходит далеко за рамки одной науки, а именно математики, и окружает нас практически везде. Таким образом, каждый человек должен знать, что такое вектор, поэтому, мы думаем, что эта тема весьма актуальна. В физике, химии, психологии, биологии, экономике и многих других науках употребляют понятие «вектор».

Цель проекта – подготовить раздел школьной энциклопедии «Вектор».

Задачами д анного проекта являются:

— познакомить с историей возникновения понятия «вектор»;

— дать понятие –вектор, продемонстрировать действий над векторами;

— показать применение векторов в решении задач по геометрии и физике;

— научить видеть необычное в обычном;

— выработать внимательное отношение к окружающему миру.

История возникновения понятия «вектор».

Одним из фундаментальных понятий современной математики является вектор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а также в технике.

Вектор относительно новое математическое понятие.

Интуитивно вектор понимается как объект, имеющий величину, направление и точку приложения. Зачатки векторного исчисления появились вместе с геометрической моделью комплексных чисел ( Гаусс, 1831).

Сам термин «вектор» впервые появился в 1845 году у ирландского математика и астронома Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем, обобщающих комплексные числа.

Гамильтону принадлежат и термин «скаляр», он определил в качестве операций над новыми объектами скалярное и векторное произведение.

Гибсс — американский физик, физикохимик, математик и механик, один из создателей векторного анализа, статистической физики, математической теории термодинамики, что во многом предопределило развитие современных точных наук и естествознания в целом.

Образ Гиббса запечатлён в «Галерее славы великих американцев». Его имя присвоено многим величинам и понятиям химической термодинамики: энергия Гиббса, парадокс Гиббса, правило фаз Гиббса, уравнения Гиббса — Гельмгольца, уравнения Гиббса — Дюгема, лемма Гиббса, треугольник Гиббса — Розебома и др.

Видео:Все типы 2 задание векторы ЕГЭ по математике профиль 2024Скачать

Почти одновременно с ним исследованиями в том же направлении занимался английский математик — Уильям Кингдон Клиффорд (1845–1879)

Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.

Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением. Например, некоторые физические величины, такие, как сила, скорость, ускорение и др., характеризуются не только числовым значением, но и направлением. В связи с этим указанные физические величины удобно изображать направленными отрезками.

Ве́ктор (от лат. vector , «несущий») — в простейшем случае математический объект , характеризующийся величиной и направлением. В геометрии вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом [1] .

Векторы также могут обозначаться малыми латинскими буквами со стрелкой (иногда — чёрточкой) над ними. Другой распространённый способ записи: выделение символа вектора жирным шрифтом.

Вектор в геометрии естественно сопоставляется переносу ( параллельному переносу ), что, очевидно, проясняет происхождение его названия ( лат. vector , несущий ).

Длина вектора – это и есть длина этого отрезка. Для обозначения длины вектора используются две вертикальные линии по обоим сторонам: |AB|.

Единичным называется вектор, длина которого равна 1. Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором. У такого вектора конец и начало совпадают. Нулевой вектор обычно обозначается как . Длина нулевого вектора, или его модуль равен нулю.

Коллинеарные вектора – вектора, которые параллельны одной прямой или которые лежат на одной прямой.

Сонаправленные вектора. Два коллинеарных вектора a и b называются сонаправленными векторами только тогда, когда их направления совпадают друг другу (направлены в одну сторону): a↑↑b

Противоположно направленные вектора – два коллинеарных вектора a и b называются противоположно направленными векторами, только когда они направлены в разные стороны: a↑↓b.

Компланарные вектора – это те вектора, которые параллельны одной плоскости или те, которые лежат на одной плоскости. С компланарными векторами мы встретимся в 10-11 классах.

Равные вектора. Вектора a и b будут равными, если они будут лежать на одной либо параллельных прямых и их направления и длины одинаковые. То есть, такой вектор можно перенести параллельно ему в каждое место плоскости. Таким образом, два вектора равны, если они коллинеарные, сонаправленые и имеют одинаковые длины:

Действия над векторами.

Суммой векторов: , …называется вектор, получающийся после ряда последовательных сложений: к вектору прибавляется вектор , к полученному вектору прибавляется вектор и так далее.

Это правило многоугольника или правило цепи, которое формулируется из правила треугольника. Из произвольного начала О откладываем вектор , из точки А ₁ , как из начала, откладываем вектор , из точки А ₂ строим вектор и так далее. Вектор есть сумма векторов .

Теорема. Для любых векторов , справедливы равенства:

1) + = + (переместительный закон).

2) ( + ) + = + ( + ) (сочетательный закон)

Эти законы сложения векторов позволяют нам находить сумму векторов в любом удобном порядке.

Умножение вектора на число

Для векторов существует три вида умножения векторов: скалярное и векторное произведение двух векторов и смешанное произведение трех векторов. Результатом первого и последнего есть число, а результатом векторного произведения – вектор.

Векторы в геометрии.

В геометрии под векторами понимают направленные отрезки. Эту
интерпретацию часто используют в компьютерной графике, строя карты освещения, с помощью нормалей к поверхностям. Так же с помощью векторов можно находить площади различных фигур, например треугольников и параллелограммов, а также объёмы тел: тетраэдра и параллелепипеда. Иногда с вектором отождествляют направление.

Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними: · = · cos . Если один из векторов нулевой, то скалярное произведение равно нулю.

Таким образом, длина (модуль) произведения векторов численно равна площади параллелограмма, построенного на векторах a и b

Смешанное произведение векторов называется скалярное произведение вектора на векторное произведение векторов и

Геометрический смысл смешанного произведения — модуль смешанного произведения численно равен объему параллелепипеда, образованного векторами ,.

Перечисленные выше свойства векторных операций во многом похожи на свойства сложения и умножения чисел. В этом состоит удобство векторных операций: вычисления с векторами выполняются по хорошо известным правилам. В то же время вектор – геометрический объект, и в определении векторных операций используются такие геометрические понятия, как длина и угол; этим и объясняется польза векторов в геометрии (и её приложений к физике и другим областям знания).

Однако для решения геометрических задач с помощью векторов необходимо прежде всего научиться «переводить» условие геометрической задачи на векторный «язык». После такого «перевода» осуществляются алгебраические вычисления с векторами, а затем полученное векторное решение снова «переводится» на геометрический «язык». В этом и состоит векторное решение геометрических задач.

C помощью векторов решаются задачи геометрии. Многие задачи не могли бы решаться иначе, либо решение их было очень затруднительным.

Приведём примеры некоторых из них:

Задача №2 Найти угол, лежащий против основания равнобедренного треугольника, если медианны, проведённые к боковым сторонам, взаимно перпендикулярны.

Задача №3 Дан равнобедренный треугольник МК N . Из вершины К проведена высота КР. Из вершин М и N проведены медианы MF и NE . КР =80, MN = 40. Найти MF и NE .

Маргарита Алигер, биография которой вызывает искренний интерес у поклонников ее творчества, – знаменитая советская поэтесса, удостоившаяся Сталинской премии второй степени за поэму «Зоя» о бесстрашном подвиге советской девушки Зои Космодемьянской. После семилетки училась в химическом техникуме. С детства писала стихи.

Векторы в физике.

О, физика, наука из наук!
Все впереди!
Как мало за плечами!
Пусть химия нам будет вместо рук,
Пусть станет математика очами .
Не разлучайте этих трех сестер,
Познания всего в подлунном мире.
Тогда лишь будет ум и глаз остер,
И знанье человеческое шире.

Векторы — мощный инструмент математики и физики. На языке векторов формулируются основные законы механики и электродинамики. Чтобы понимать физику, нужно научиться работать с векторами. В физике, как и в математике, вектор – это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей.

Немецкий физик, математик и филолог. (1809-1877)

В области физики Грассману принадлежат работы по акустике и магнитному взаимодействию токов. Общие идеи Грассмана об абстрактных векторных пространствах привели его к открытию
важного положения – возможности рассматривать цветовые ощущения как трехмерные векторы, что лежит в основе современного учения о цвете. (Чёрный цвет имеет координаты (0,0,0), каждому цвету можно поставить в соответствие координаты точки трёхмерного пространства.
Интерпретация вектора, как параллельного переноса, позволяет естественным и интуитивно очевидным способом ввести операцию сложения векторов — как композиции (последовательного

применения) двух (или нескольких) переносов; то же касается и операции умножения вектора на число .

Джеймс Клерк Максвелл — английский физик, создатель классической электродинамики, один из
основоположников статистической физики, выдвинул идею электромагнитной природы света, установил первый статистический закон — закон распределения молекул по
скоростям, названный его именем. Альберт Эйнштейн однажды сказал, что » работа Джеймса клерка Максвелла изменила мир навсегда. «Действительно, Максвелл предоставил первую цветную фотографию и заложил основу для будущего развития телевизионных, радиолокационных, микроволновых и инфракрасных технологий.
Но в каждом учебном предмете вектор рассматривается так, как это удобно для изучаемого вопроса, но суть – одна.

Проведём сравнительный анализ понятия “вектор” и действий над векторами в математике и физике.

Мальчик массой 50 кг, стоя на гладком льду, бросает груз массой

8 кг под углом 60 0 к горизонту со скоростью 5 м/с. Какую скорость приобретет мальчик?

На парашютиста массой 90 кг в начале прыжка действует сила сопротивления воздуха, проекции которой на оси координат Х и Y равны 300 Н и 500 Н. Найти равнодействующую всех сил.

Вектор используются везде, даже там, где мы их не замечаем, например в литературе : вспомним басню Ивана Андреевича Крылова о том, как «лебедь, рак да щука везти с поклажей воз взялись». Басня утверждает, что «воз и ныне там», другими словами, что равнодействующая всех сил приложенных к возу равна нулю. А сила, как известно, векторная величина.

В химии. Нередко даже великими учеными высказывалась мысль, что химическая реакция является вектором. Вообще-то, под понятие «вектор» можно подвести любое явление. Вектором выражают действие или явление, имеющее четкую направленность в пространстве и в конкретных условиях, отражаемое его величиной. Направление вектора в пространстве определяется углами, образующимися между вектором и координатными осями, а длина (величина) вектора – координатами его начала и конца. Однако утверждение, что химическая реакция является вектором, до сих пор было неточно. Тем не менее, основой этого утверждения служит следующее правило: «Любой химической реакции отвечает симметричное уравнение прямой в пространстве с текущими координатами в виде количеств веществ (молей), масс или объемов».

Вектором (в биологии) называется организм, переносящий паразита от одного организма-хозяина к другому. Например, вши переносят возбудителей сыпного тифа, крысы – чумы. Вектор (в генетике) — молекула нуклеиновой кислоты, чаще всего ДНК, используемая в генетической инженерии для передачи генетического материала другой клетке.

Векторы в экономике

Одним из разделов высшей математики является линейная алгебра. Ее элементы широко применяются при решении разнообразных задач экономического характера. Среди них важное место занимает понятие вектора. Вектор представляет собой упорядоченную последовательность чисел. Числа в векторе с учетом их расположения по номеру в последовательности называются компонентами вектора. Отметим, векторы можно рассматривать в качестве элементов любой природы, в том числе и экономической. Предположим, что некоторая текстильная фабрика должна выпустить в одну смену 30 комплектов постельного белья, 150 полотенец, 100 домашних халатов, тогда производственную программу данной фабрики можно представить в виде вектора, где всё, что должна выпустить фабрика – это трехмерный вектор.

Векторы в психологии

На сегодняшний день имеется огромное количество информационных источников для самопознания, направлений психологии и саморазвития. И не трудно заметить, что все больше обретает популярность такое необычное направление, как системно-векторная психология, в ней существует 8 векторов. Системно-векторная психология позиционируется не как отрасль классической психологии или определенное течение, а как отдельная наука изучения типологии личности.

Вектор – это симбиоз физиологических и психологических качеств человека. Это — характер, темперамент, здоровье, привычки индивида.

Векторы в повседневной жизни

Мы обратили внимание, что векторы, помимо точных наук, встречаются нам каждый день, т.е. повседневно. Векторы – указатели, которые помогают нам быстро найти тот или иной объект, отдел и сэкономить время, или стрелки дорожных знаков.

Базовое понятие «вектор», рассмотренное нами на уроках геометрии в 9 классе, является основой для изучения, а главное понимания других школьных предметов: физики, химии, биологи, экономики. Мы считаем, что этот раздел математики очень пригодится тем, кто планирует получать образование в любой профессии.

1. Векторы необходимы нам для изучения не только математики, но и других наук.

2. Каждый образованный человек должен знать, что такое вектор, потому что сталкивается с этим понятием не только во время учёбы, но и в повседневной жизни.

Учебник Геометрия 7-9 авторы Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев, Е.Г. Позняк, И.И. Юдина; издательство «Просвещение» 2016

Геометрия: задачи на готовых чертежах для подготовки к ГИА и ЕГЭ: 7-9/Э.Н. Балаян. Изд. 7-е –Ростов н/Д; Феникс, 2015.

Энциклопедический словарь юного математика для среднего и старшего школьного возраста.

Составитель А.П. Савин.- М.: Педагогика,, 1985.-352 с.,ил.

http ^// gruzdoff . ru / wiki /Вектор (математика)

🎥 Видео

Как проецировать вектора за 1 минуту?! | ЕГЭ по физике | Саня Эбонит | 100балльный репетиторСкачать